动态规划算法
动态规划算法介绍
- 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分成小问题进行解决,从而一步步获取最优解的处理算法。
- 动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
- 与分治算法不同的是,
适用于动态规划求解的问题,经分解得到的子问题往往不是互相独立的。(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)。 - 动态规划可以通过
填表的方式来逐步推进,得到最优解。
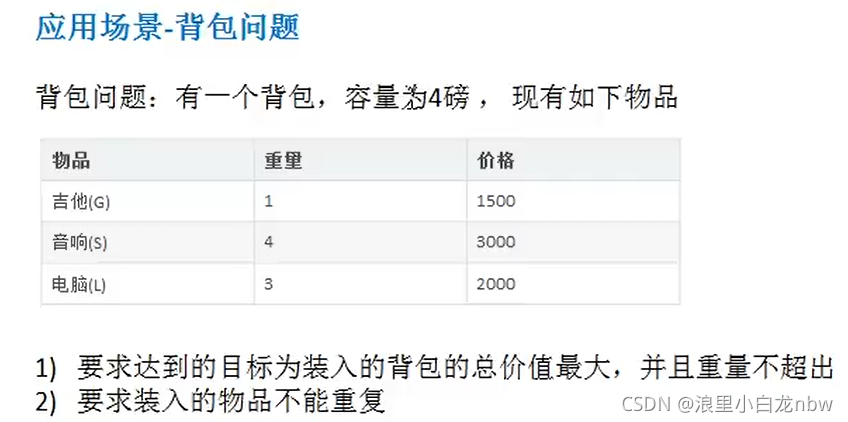
01背包问题
01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W2至Wn,与之相对应的价值为P1,P2至Pn。01背包的约束条件是给定几种物品,每种物品有且只有一个,并且有权值和体积两个属性。在01背包问题中,因为每种物品只有一个,对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中,则不需要处理。如果选择将其放入背包中,由于不清楚之前放入的物品占据了多大的空间,需要枚举将这个物品放入背包后可能占据背包空间的所有情况。
思路一:图标填充
填表过程:
从物品一开始,先行再列
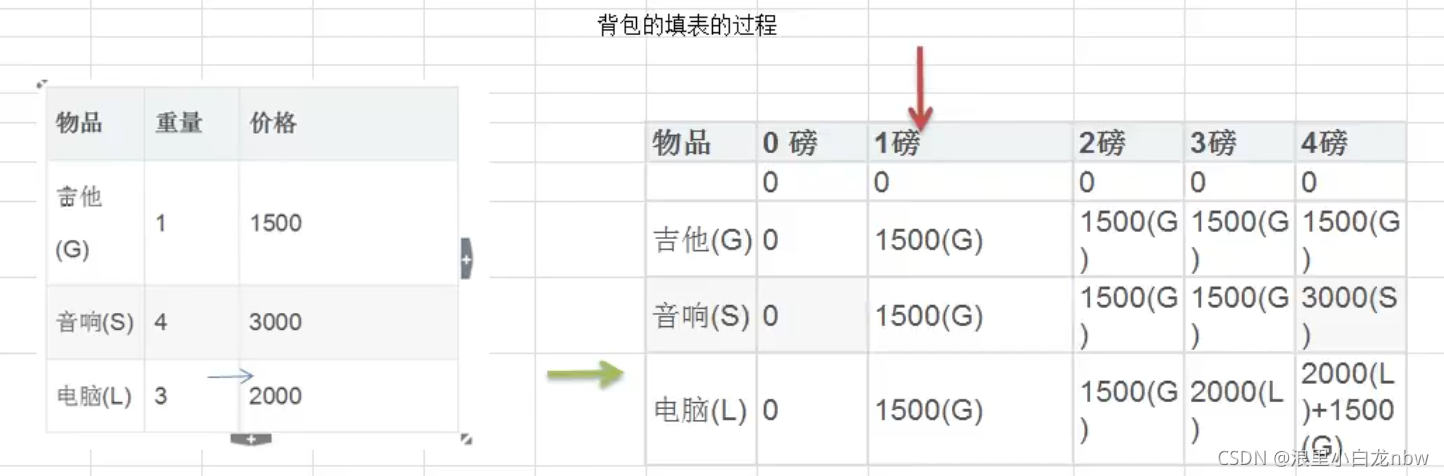
经过填表后可得出如下:

- v[i][0]=v[0][j]=0 //表示填入表第一行和第一列是0
- 当w[i]>j时:v[i][j]=v[i-1][j] //当准备加入新增的商品的容量大于当前背包的容量时,就直接使用上一个单元格的装入策略
- 当j>=w[i]时:v[i][j]=max{v[i-1][j],v[i]+v[i-1][j-w[i]]}
当准备加入的新增的商品的容量小于当前背包的容量,
装入方式:
v[i-1][j]表示上一个单元格的装入的最大值
v[i-1][j-w[i]]表示装入i-1个商品(不包括当前商品),剩余空间j-w[i]的最大值
注意: 具体的动态规划算法多种多样,但它们具有相同的填表格式
思路二:分析图
问题描述:
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
针对此题我们画出分析图:

注:
- f(i,j)表示,在满足从前i个物品中选,体积不超过j的集合(各种选法的集合),f(i,j)的值表示集合中的价值最大值(属性为max)
- f(i,j)表示集合中的某种属性(值),集合中有很多选法,但是到最后要落实到值上面
相关代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int f[N][N];
int v[N],w[N];
int main(){
int m,n;
cin>>m>>n;
for(int i=1;i<=m;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=m;i++){
for(int j=0;j<=n;j++){
f[i][j]=f[i-1][j];
if(v[i]<=j) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
cout<<f[m][n];//答案即为最后一个物品尝试过,并且为背包的容积
return 0;
}
优化(滚动数组存储最大值,因为后一层的求解依赖于前一层)
相关代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}