[数据结构与算法]剑指 Offer II 020. 回文子字符串的个数

剑指 Offer II 020. 回文子字符串的个数

给定一个字符串 s ，请计算这个字符串中有多少个回文子字符串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

动态规划

对于一个子串而言，如果它是回文串，并且长度大于 2 , 那么将它首尾的两个字母去除之后，它仍 然是个回文串。例如对于字符串 “ababa”, 如果我们已经知道 “bab" 是回文串，那么 "ababa"一定 是回文串， 这是因为它的首尾两个字母都是 “a”。

根据这样的思路，我们就可以用动态规划的方法解决本题。

第 1 步：定义状态

我们用 $dP(i,j)$? 表示字符串 $s$? 的第 $i$? 到 $j$? 个字母组成的串 (下文表示成 $s[i:j])$?? 是否为回文串:
$$dP(i,j)=\{\begin{array}{ll}\text{?true,?}& \text{?如果子串?}{S}_i\dots S_j\text{?是回文串?}\\ \text{?false,?}& \text{?其它情况?}\end{array}$$
这里的「其它情况」包含两种可能性：

• $s[i,j]$ 本身不是一个回文串;
• $i>j$, 此时 $s[i,j]$? 本身不合法。

第 2 步：思考状态转移方程

整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。

• 当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

• 当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

  • 下标i 与 j相同，同一个字符例如a，当然是回文子串

  • 下标i 与 j相差为1，例如aa，也是文子串

  • 下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1] 是否为true。

那么我们就可以写出动态规划的状态转移方程:
$$dP(i,j)=dP(i+1,j?1)and\left(S_i==S_j\right)$$
也就是说，只有 $s[i+1:j?1]$ 是回文串，并且 $s$ 的第 $i$ 和 $j$ 个字母相同时, $s[i:j]$? 才会是回文串。

第 3步：确定遍历顺序

首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。

dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：

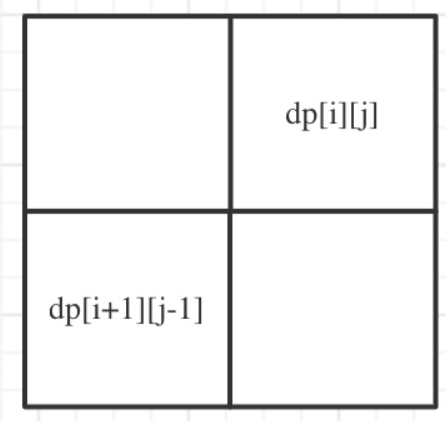
• 「动态规划」的「自底向上」求解问题的思路，很多时候是在填写一张二维表格。由于 s[i..j] 表示 s 的一个子串，因此 i 和 j 的关系是 i <= j，只需要填这张表格对角线右上半部分；

  所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

举例，输入：“aaa”，dp[i][j]状态如下：

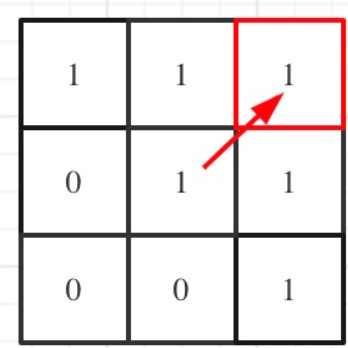
图中有6个true，所以就是有6个回文子串。

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n^2)$

class Solution:
    def countSubstrings(self, s: str) -> int:
        n = len(s)
        dp = [[False]* n for _ in range(n) ]
        result = 0
        for i in range(n-1,-1,-1):# 自底向上
            for j in range(i,n):
                if s[i] == s[j]:
                    if j - i <= 1: #情况一 和 情况二
                        result += 1
                        dp[i][j] = True
                    elif dp[i+1][j-1]: #情况三
                        result += 1
                        dp[i][j] = True
        return result

双指针

动态规划的空间复杂度是偏高的，我们再看一下双指针法。

首先确定回文串，就是找中心然后想两边扩散看是不是对称的就可以了。

在遍历中心点的时候，要注意中心点有两种情况。

一个元素可以作为中心点，两个元素也可以作为中心点。

那么有人同学问了，三个元素还可以做中心点呢。其实三个元素就可以由一个元素左右添加元素得到，四个元素则可以由两个元素左右添加元素得到。

所以我们在计算的时候，要注意一个元素为中心点和两个元素为中心点的情况。

这两种情况可以放在一起计算，但分别计算思路更清晰，我倾向于分别计算，代码如下：

class Solution:
    def countSubstrings(self, s: str) -> int:
        result = 0
        n = len(s)
        for i in range(n):
            #通过遍历每个回文中心，向两边扩散，并判断是否回文字串
            result += self.extend(s, i, i, n) #以i为中心
            result += self.extend(s, i, i+1, n) #以i和i+1为中心
        return result

    def extend(self, s, i, j, n):
        res = 0
        while i >= 0 and j < n and s[i] == s[j]:
            #如果当前是一个回文串，则记录数量
            i -= 1 #向两边扩散
            j += 1
            res += 1
        return res