[数据结构与算法]CCF CSP 202104-2 邻域均值 C++（100分）

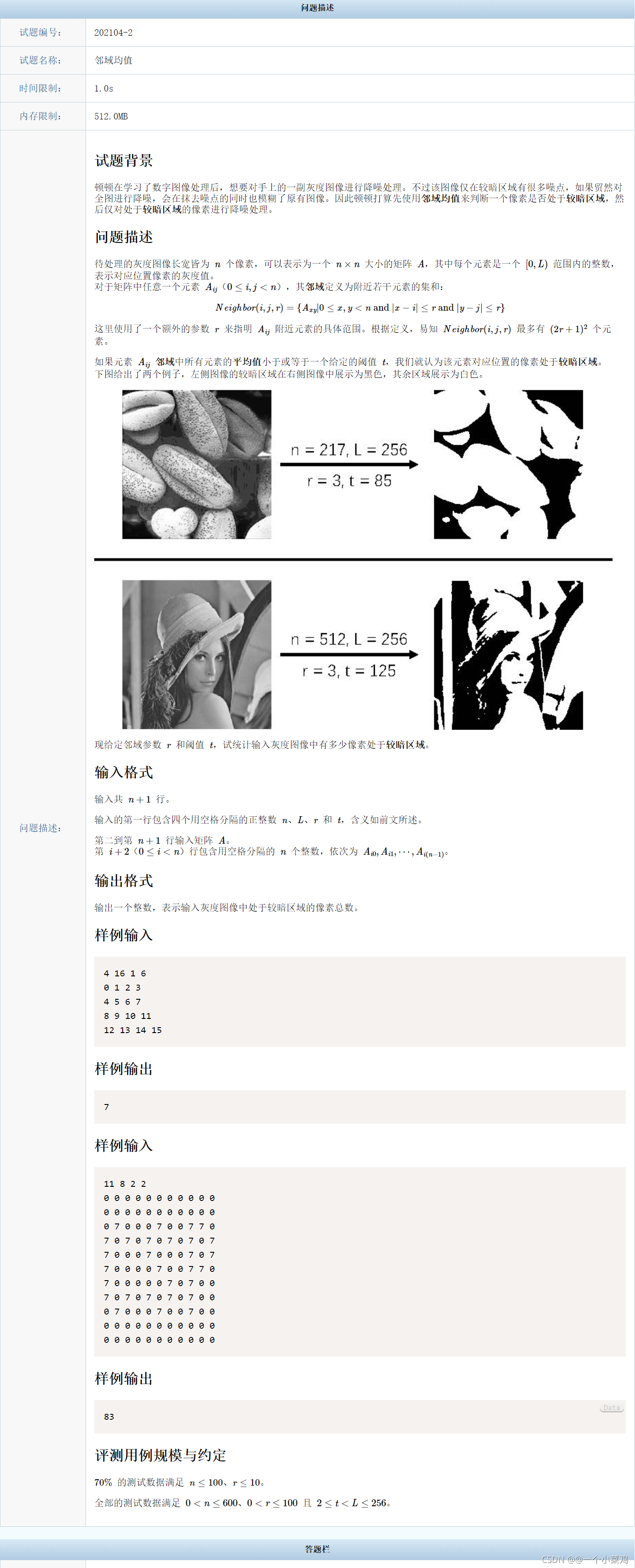
刚开始用的是暴力求解方法，简单分析可以知道，任意一个点的邻域均为矩形，所以可以用左上角顶点和右下角顶点来确定邻域的范围，如下：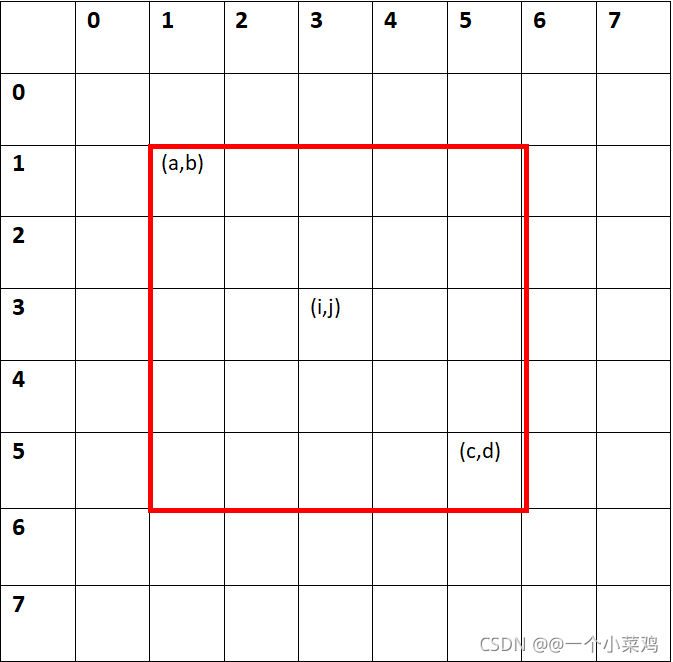
每次循环前先判断a,b,c,d的取值，然后直接计算方框内的数，结果只有70分，报告显示超时，所以必须优化算法。
后面发现，同一行两个相邻数之间最多只有两列数不同，如下：

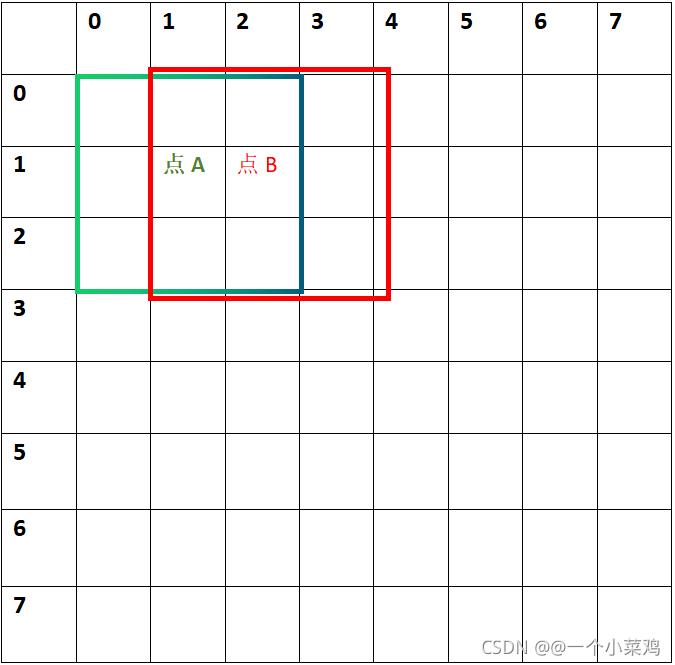
所以优化后的算法就是每行只算第一个元素的sum值，然后后面的n-1个数的sum值都根据前面的sum值来计算，即减去图中第0列的数，加上第3列的数。每次循环下来都能减少很多计算量。

#include<iostream>

using namespace std;
int max(int n, int m)
{
	if (n > m)
		return n;
	else
		return m;
}
int min(int n, int m)
{
	if (n < m)
		return n;
	else
		return m;
}
int main()
{
	int** arr;
	int n, L, r, t;
	int a, b, c, d;
	int sum;
	int count = 0;//处于较暗位置的像素点个数
	cin >> n >> L >> r >> t;
	arr = new int* [n];
	for (int i = 0; i < n; i++)
		arr[i] = new int[n];
	for (int i = 0; i < n; i++)//输入n*n方阵
		for (int j = 0; j < n; j++)
			cin >> arr[i][j];
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (j == 0)//计算每行第一个元素的邻域
			{
				sum = 0;
				a = max(0, i - r);
				c = min(i + r, n - 1);
				b = max(0, j - r);
				d = min(j + r, n - 1);
				for (int x = a; x <= c; x++)
					for (int y = b; y <= d; y++)
						sum = sum + arr[x][y];
			}
			else
			{
				b = max(0, j - r);
				d = min(j + r, n - 1);
				if (j + r < n)
				{
					if (j - r > 0)
						for (int x = a; x <= c; x++)
							sum = sum - arr[x][j - r - 1];
					for (int x = a; x <= c; x++)
						sum = sum + arr[x][j + r];
				}
				else
					for (int x = a; x <= c; x++)
						sum = sum - arr[x][j - r - 1];
			}
			if (sum <= t * (c - a + 1) * (d - b + 1))
				count++;
		}
	}
	cout << count << endl;
	delete[]arr;
	return 0;
}