赫夫曼
基本介绍
- 1) 给定 n 个权值作为 n 个叶子结点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树。
- 2) 赫夫曼树是带权路径长度最短的树,权值较大的结点离根较近
赫夫曼树几个重要概念和举例说明
- 1) 路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为 1,则从根结点到第 L 层结点的路径长度为 L-1
- 2) 结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积
- 3) 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为 WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
- 4) WPL 最小的就是赫夫曼树

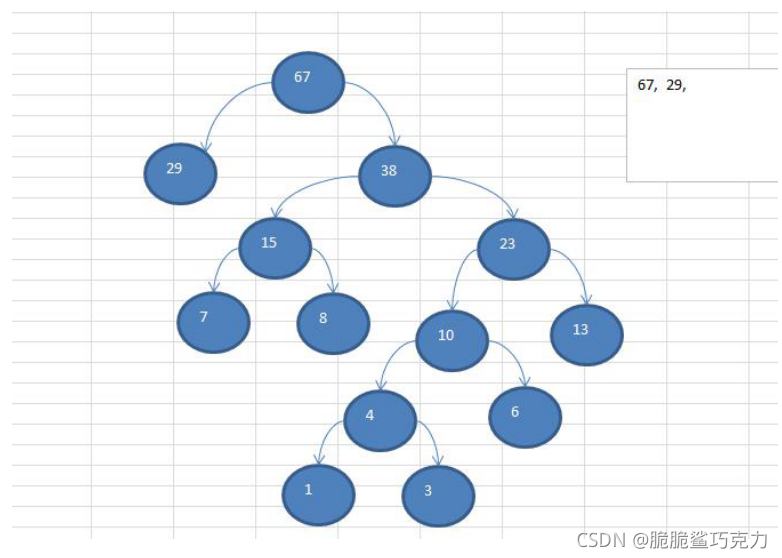
赫夫曼树创建思路图解
构成赫夫曼树的步骤:
- 1) 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 2) 取出根节点权值最小的两颗二叉树
- 3) 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 4) 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一颗赫夫曼树
public class Huffman {
public static void main(String[] args) {
int[] arr = {13, 7, 8, 3, 29, 6, 1};
preOrder(createHuffmanTree(arr));
}
public static void preOrder(HuffmanNode node){
System.out.println(node);
if (node.getLeft() != null){
preOrder(node.getLeft());
}
if (node.getRight() != null){
preOrder(node.getRight());
}
}
/**
* 创建哈夫曼树
* @param arr
* @Return 返回顶上的节点
*/
public static HuffmanNode createHuffmanTree(int[] arr){
//1.遍历arr数组
//2.将arr每个元素构建成一个HuffmanNode
//3.将HuffmanNode放到ArrayList中
List<HuffmanNode> nodes = new ArrayList<>();
for (int i: arr) {
nodes.add(new HuffmanNode(i));
}
while (nodes.size() > 1){
//对nodes进行排序,因为实现了Comparable接口,所以可以直接调用排序
Collections.sort(nodes);
//取出根节点权值最小的两颗二叉树
//把这两颗二叉树组合成一颗新的二叉树
HuffmanNode left = nodes.get(0);
HuffmanNode right = nodes.get(1);
//构建一颗新的二叉树
HuffmanNode parent = new HuffmanNode(left.getValue()+right.getValue());
parent.setLeft(left);
parent.setRight(right);
//从ArrayList中删除处理过的二叉树
nodes.remove(left);
nodes.remove(right);
nodes.add(parent);
}
return nodes.get(0);
}
}
//创建哈夫曼树节点类
//为了让HuffmanNode对象持续排序Collections集合排序
//让Node实现Comparable接口
class HuffmanNode implements Comparable<HuffmanNode>{
//节点权值
private int value;
private HuffmanNode left; //左子节点
private HuffmanNode right; //右子节点
public HuffmanNode getLeft() {
return left;
}
public void setLeft(HuffmanNode left) {
this.left = left;
}
public HuffmanNode getRight() {
return right;
}
public void setRight(HuffmanNode right) {
this.right = right;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public HuffmanNode(int value) {
this.value = value;
}
@Override
public String toString() {
return "HuffmanNode{" +
"value=" + value +
'}';
}
@Override
public int compareTo(HuffmanNode o) {
//表示从小到大进行排序
return this.value - o.value;
}
}
赫夫曼编码
基本介绍
- 1) 赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法
- 2) 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
- 3) 赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在 20%~90%之间
- 4) 赫夫曼码是可变字长编码(VLC)的一种。Huffman 于 1952 年提出一种编码方法,称之为最佳编码
用赫夫曼编码进行压缩
????????实现方式上和赫夫曼树大同小异,区别在于Node,Node需要保存权值和Data,权值用来保存Data在文本里出现的频率。
class Node implements Comparable<Node>{
Byte data; //存放数据本身
int weight; //权值,表示字符出现次数
Node left;
Node right;
public Byte getData() {
return data;
}
public void setData(Byte data) {
this.data = data;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//从小到大排序
return this.weight - o.weight;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
}
public static void main(String[] args) {
String str = "i like like like java do you like a java";
byte[] contentBytes = str.getBytes();
List<Node> nodes = getNodes(contentBytes);
preOrder(createHuffman(nodes));
}
/**
* 建立一个Huffman树
* @param nodes
* @return
*/
private static Node createHuffman(List<Node> nodes){
while (nodes.size() > 1){
//对nodes进行排序,因为实现了Comparable接口,所以可以直接调用排序
Collections.sort(nodes);
//取出根节点权值最小的两颗二叉树
//把这两颗二叉树组合成一颗新的二叉树
Node left = nodes.get(0);
Node right = nodes.get(1);
//构建一颗新的二叉树,它没有data,只能有权值
Node parent = new Node(null,left.getWeight()+right.getWeight());
parent.setLeft(left);
parent.setRight(right);
//从ArrayList中删除处理过的二叉树
nodes.remove(left);
nodes.remove(right);
nodes.add(parent);
}
return nodes.get(0);
}
/**
* 将字节数组转成数组
* @param bytes 接受一个字节数组
* @return 返回一个List,里面记录了每个字母的出现频率,采用key-value的方式保存
*/
private static List<Node> getNodes(byte[] bytes){
List<Node> nodes = new ArrayList<>();
//统计每一个bytes出现的次数 然后put进map
Map<Byte,Integer> counts = new HashMap<>();
for (byte b: bytes) {
if (!counts.containsKey(b)){ //如果没有这个key那就put进去
counts.put(b,1);
}else {
counts.put(b,counts.get(b)+1) ; //有的话直接+1
}
}
//把每一个key-value转成一个node对象并加入nodes集合里
for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(),entry.getValue()));
}
return nodes;
}上面已经生成了赫夫曼树,接下来要生成对应的赫夫曼编码
//将赫夫曼编码表存放在Map中
static Map<Byte, String> huffmanCodes = new HashMap<>();
//在生成赫夫曼编码表时,需要去拼接路径。定义一个Stringbuilder来存储某个叶子节点的路径
static StringBuilder builder = new StringBuilder();
/**
* 将传入的node节点的所有叶子节点的赫夫曼编码得到,并放入到huffmanCodes集合里
*
* @param node 传入的节点,默认从根节点传
* @param code 路径:左子节点为0 右子节点为1
* @param builder 拼接路径
*/
private static void getCodes(Node node, String code, StringBuilder builder) {
StringBuilder builder2 = new StringBuilder(builder);
//将code加入builder2
builder2.append(code);
if (node != null) { //node为空就不处理了
//判断当前node是叶子节点还是非叶子节点
if (node.data == null) { //代表是非叶子节点
//递归处理
//向左
getCodes(node.left, "0", builder2);
//向右递归
getCodes(node.right, "1", builder2);
} else {
//表示找到了一个叶子节点的最后
huffmanCodes.put(node.data, builder2.toString());
}
}
}
完成生成
接下来做最后的工作,将字符串对应的byte[]通过生成的赫夫曼编码表,返回一个压缩后的byte数组
/**
* 将字符串对应的byte[]通过生成的赫夫曼编码表,返回一个压缩后的byte数组
* @param bytes 原始字符串对应的bytes
* @param huffmanCodes 生成的huffman编码Map
* @return 返回赫夫曼编码处理过后的byte[]
*/
private static byte[] zip(byte[] bytes,Map<Byte,String> huffmanCodes){
//1。利用huffmanCOdes将bytes转换成赫夫曼编码对应的字符串
StringBuilder builder = new StringBuilder();
//遍历bytes数组
for (byte b: bytes){
builder.append(huffmanCodes.get(b));
}
//将builder保存的内容转为byte[]
//统计返回byte[] huffmanCodeBytes 长度
int len = (builder.length() + 7) / 8; //这句话等价与下面这个ifelse
// if (builder.length() % 8 == 0){
// len = builder.length() / 8;
// }else {
// len = builder.length() / 8 + 1;
// }
//创建一个存储压缩后的byte数组,为了8位8位的放!!
byte[] huffmanCodeBytes = new byte[len];
int index = 0;
//因为是每8位对应一个byte,所以步长应该是+8
for (int i = 0; i < builder.length(); i+=8) {
String strByte;
if (i+8 > builder.length()){
strByte = builder.substring(i);
}else {
strByte = builder.substring(i, i + 8);
}
//将strByte转成一个byte数,放入by里
huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte,2);//将byte转成二进制
index++;
}
//返回最终的结果
return huffmanCodeBytes;
}整体逻辑:得到一个字符串,统计每个字母出现的频率存入Node里并转换成一颗赫夫曼树。再将这颗赫夫曼树转换成赫夫曼编码(key=字母,value=赫夫曼编码)。再把赫夫曼编码归拢并按8byte8byte分,将byte转换成int后转存到一个数组里。即完成了压缩。
二叉排序树(BST)
基本介绍:
??? 二叉排序树BST(Binary Sort(Search) Tree),对于二叉排序树的任何一个非叶子节点要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大。
??? 特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点,如果二叉排序树中存在节点值相同的时候,示例代码中给出的获取节点的方法,只会返回第一个相同值的节点,这就致使在进行删除操作的时候会报栈溢出(StackOverflowError),所以,二叉排序中尽量避免值相同的情况
??? 针对数组{7,3,10,12,5,1,9}对应的排序二叉树如下:
???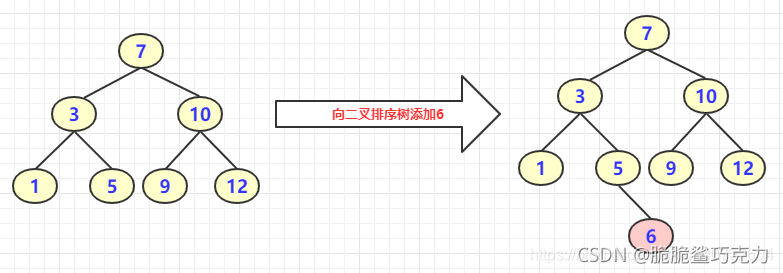
??? BST添加(添加逻辑详见示例代码)完成后,通过中序遍历一定是有序的
???
————————————————
版权声明:本文为CSDN博主「木易三水良」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_40722604/article/details/104507484
基本实现:
??????? 添加+中序遍历
package shangguigu2.二叉排序树;
public class BinarySortTreeDemo {
public static void main(String[] args) {
BinarySortTree tree = new BinarySortTree();
int[] arr = {7,3,10,12,5,1,9};
for (int value : arr) {
tree.add(new Node(value));
}
tree.infixOrder();
}
}
class BinarySortTree{
//根节点
private Node root;
/**
* 二叉排序树-添加节点
* @param node
*/
public void add(Node node){
if (root == null){
root = node;
return;
}
root.add(node);
}
public void infixOrder(){
if (root != null){
root.infixOrder();
}else {
throw new RuntimeException("root节点为空不允许遍历!");
}
}
}
class Node{
private int value;
private Node left;
private Node right;
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
/**
* 递归的形式添加节点,前提是需要满足二叉排序树的要求
* @param node
*/
public void add(Node node){
if (node == null){
return;
}
//判断传入节点的值和当前子树的根节点的值之间的关系
if(node.value < this.value){
//如果当前节点的左子节点为空,那node直接挂到当前节点的左子节点
if (this.left == null){
this.left = node;
}else {
//递归的向左子树添加
this.left.add(node);
}
}else{
//添加节点的值大于当前节点的值
if (this.right == null){
//将当前的值挂在右子节点
this.right = node;
}else {
//递归的向右添加
this.right.add(node);
}
}
}
/**
* 中序遍历
*/
public void infixOrder(){
if (this.left != null){
this.left.infixOrder();
}
System.out.println(this.value);
if (this.right != null){
this.right.infixOrder();
}
}
}
?二叉树的删除:
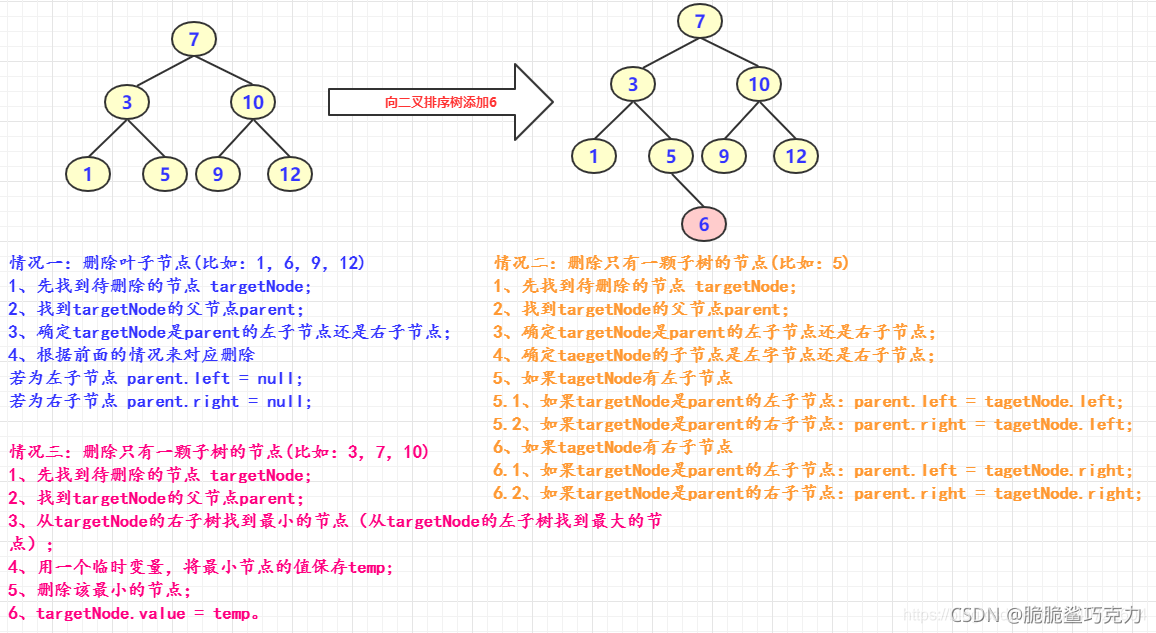
下面这张图可以用来理解第三种情况

?以下是实现代码:
/**
* 返回以Node为根节点的二叉排序树的最小节点的值
* 删除以Node为根节点的二叉排序树的最小节点
*
* @param node 当作二叉排序树的根节点
* @return 以Node为根节点的二叉排序树的最小节点的值
*/
public int delRightTreeMin(Node node) {
Node target = node;
//循环的查找左节点,直到找到最小值
while (target.getLeft() != null) {
target = target.getLeft();
}
//target此时指向了最小节点
//删除最小节点
delNode(target.getValue());
return target.getValue();
}
/**
* 二叉排序树-删除
*
* @param value
*/
public void delNode(int value) {
if (root != null) {
//1.先去找到要删除的节点target
Node target = search(value); //找到要删除的节点
//如果没有找到要删除的节点
if (target == null) {
return;
}
//如果发现二叉排序树只有一个节点,那直接删除这颗树即可
if (root.getLeft() == null && root.getRight() == null) {
root = null;
return;
}
//找到target的父节点
Node parent = searchParent(value);
//如果要删除的节点是叶子节点
if (target.getLeft() == null && target.getRight() == null) {
//判断是删除左子节点还是右子节点 首先进行非空判断 再比较值
if (parent.getLeft() != null && target.getValue() == parent.getLeft().getValue()) {
parent.setLeft(null);
} else if (parent.getRight() != null && target.getValue() == parent.getRight().getValue()) {
parent.setRight(null);
}
} else if (target.getLeft() != null && target.getRight() != null) { //在这里进行第三种情况的删除 删除有两个节点的非叶子节点
int minVal = delRightTreeMin(target.getRight());
target.setValue(minVal);
} else { //删除只有一颗子树的节点
//如果target是有左子节点
if (target.getLeft() != null) {
if (parent != null) { //防止出现还剩两个节点时删除根节点,但是根节点已经没有有父节点了,只剩下左右子树,这时候让root指向左子树或者右子树
//判断target是parent的左子节点
if (parent.getLeft().getValue() == target.getValue()) {
parent.setLeft(target.getLeft());//把target的左子节点替换到parent的左子节点
} else { //target是parent的右子节点
parent.setRight(target.getLeft());//同样直接放在parent的左子节点就好
}
} else {
root = target.getLeft();
}
} else { //如果target是有右子节点
if (parent != null) {
//假设target是parent的左子节点
if (parent.getLeft().getValue() == value) {
parent.setLeft(target.getRight()); //让right替换target
} else { //假设target是parent的右子节点
parent.setRight(target.getRight()); //那就让target的right替换target
}
} else {
root = target.getRight();
}
}
}
}
}
/**
* 查找要删除的节点
*
* @param value 希望删除的节点的值
* @return 如果找到返回该节点,否则返回null
*/
public Node search(int value) {
if (value == this.value) { //找到该节点,直接返回
return this;
} else if (value < this.value) { //根据value大小向左或向右递归查找
if (this.left == null) { //如果左子树已经为空了,那就没必要找了
return null;
}
return this.left.search(value);
} else {
if (this.right == null) {//如果右子树已经为空了,那就没必要找了
return null;
}
return this.right.search(value);
}
}
/**
* 查找要删除节点的父节点
*
* @param value 要查找的值
* @return 要删除节点的父节点,如果没有则返回null
*/
public Node searchParent(int value) {
//判断当前节点的子节点是否是要找的值,如果是则返回自己
if ((this.left != null && this.left.value == value)
||
(this.right != null && this.right.value == value)) {
return this;
} else {
//如果查找的值小于当前节点的值,且当前节点的左子节点不为空
if (value < this.value && this.left != null) {
return this.left.searchParent(value); //向左子树递归查找
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); //向右子树递归查找
} else {
return null; //什么条件都不满足那就等于找不到
}
}
}????