10.2 计数与概率基础
就是排列组合啦······
加法原理
做一件事情有n个办法,第i个办法有pi种方案,则一共需要p1+p2+······pn种方案。
乘法原理
做一件事情有n个步骤,第i个步骤有pi种方案,则一共有p1p2······pn种方案。
容斥原理
这里书上这里写的不好:
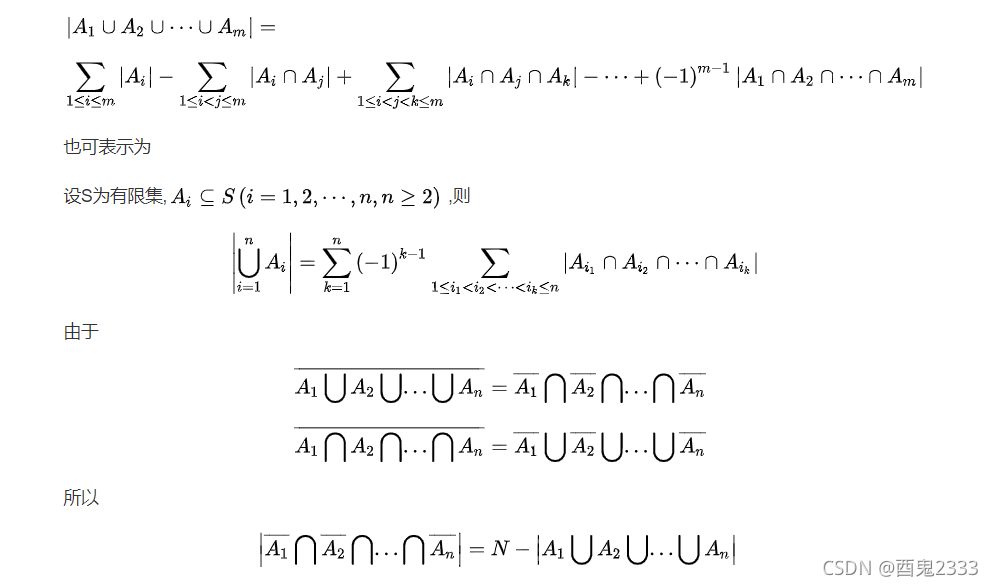
(截自百度百科,证明过程一般分为计次数和归纳法两种,这里不多作赘述)
有重复元素的全排列
有k个元素,其中第i个元素有ni个,求全排列的个数。
分析:没啥好分析的,这个有高中学历的其实都知道hhhh,答案为(n1+n2+n3·······nk)!/(n1!n2!n3!······nk!)。
可重复选择的组合
有n个不同元素,每个元素可以重复选择多次,一共选k个元素,有多少种选法?
分析:我们假设第i个元素选择了xi次,相当于求:x1+x2······+xn=k (xi都为自然数)的解的个数。如果都是正整数,那么这个问题显然用“插板法”就可以非常轻松的解决了。于是我们另yi=xi+1,则相当于求:y1+y2······+yn=n+k (yi都为正整数)的解的个数。那这个问题的答案就很简单了,n+k-1个空格插n-1个板,答案为C(n+k-1,n-1)。
10.2.1 杨辉三角与二项式定理
也是高中学过的知识点,两个图分别代表杨辉三角的两个性质:

组合数性质:

这里没什么重点要提的,唯一可能有点重要的就是用递推的方法去求C(n,k)的值,代码如下:
C[0]=1;//表示C(n,0)=1
for (int i=1;i<=k;i++) C[i]=C[i-1]*(n-i+1)/i;
10-6 无关的元素 (UVA 1635)
对于给定的n个数a1,a2······an,依次求出相邻两数之和来得到一个新数列。重复上述操作,最后结果将变成一个数。问这个数除以m的余数与哪些数无关?
例如n=3,m=2时,求和得到的即是a1+2a2+a3,这个结果除以m的余数与a2无关。
分析:显然最终的结果即是:C(n-1,0)*a1+C(n-1,1)*a2+C(n-1,2)*a3·······+C(n-1,n-1)*an。如果结果除以m的余数与ai无关,那么C(n-1,i-1)除以m的余数一定为0。于是这个问题就变成了判断C(n-1,0),C(n-1,1)······C(n-1,n-1)中哪些是m的倍数。
这个问题用上面介绍过的递推的方法就可以了(但在做除法的时候会有一些细节问题需要处理)。
10.2.2 数论中的计数问题
约数的个数
给出正整数n的唯一分解式n=p1a1p2a2p3a3···pkak,求n的正约数的个数。
分析:显然,n的任意正约数,将他转化为唯一分解形式,一定不会产生新的素因子,也就是说一定肯定表示成p1b1p2b2p3b3···pkbk的形式,bi可以是0,1,2······ai共ai+1种情况,而且不同的素因子之间保持相护独立的关系。于是有n的正约数的个数为:
(a1+1)(a2+1)(a3+1)·······(ak+1)
小于n且与n互素的数
给出正整数n的唯一分解式n=p1a1p2a2p3a3···pkak,求1-n中与n互素的数的个数T。
分析:我们用Si表示1-n中被pi整除的数的集合,那么我们可以得到:
T=n-|S1∪S2∪S3······Sk| (1-n中与n互素的数就是1-n中不被n的素因子整除的数)
看到|S1∪S2∪S3······Sk|,我们可以很自然地想到上面提到的容斥原理:
于是|S1∪S2∪S3······Sk|=|S1|+|S2|······|Sk|-|S1∩S2|-|S1∩S3|-|S1∩S4|·······(比较麻烦就不写全了)
那么我们怎么计算类似于|S1∩S3∩S4|的值呢?事实上S1∩S3∩S4表示1-n中被p1,p3和p4整除的数,由于pi都是素数,于是|S1∩S3∩S4|的值即是n/(p1*p3*p4),于是我们可以将上面的并集交集的元素个数统统按照上面的形式进行转化,最后转化为以下的公式(这个公式的转化并不显然,需要一定的数学基础):
T=n(1-1/p1)(1-1/p2)······(1-1/pk),T我们往往称为n的欧拉函数值。
欧拉函数的代码如下:
int euler_phi(int n){int m=(int)sqrt(n+0.5),ans=n;
for (int i=2;i<=m;i++) if (n%i==0){//欧拉函数的处理
ans=ans/i*(i-1); while (n%i==0) n/=i;//减小搜索范围
} if (n>1) ans=ans/n*(n-1);//其实我没有想到除了质数什么时候会出现这种情况
}
如果是求1-n的所有数的phi值,就会用一种类似于筛法的做法:
void phi_table(int n,int* phi){memset(phi,0,sizeof(phi)); phi[1]=1;
//双层循环内判断的phi[i]=0不仅表示i还没有进行欧拉函数的计算,还表示i是素数
//两层循环相当于做了一遍筛法,同时将欧拉函数求因子的步骤换了角度做了一遍(这个比较抽象)
//j代表大于等于i的i的倍数,由于i是素数,那么i一定是j的一个素因子,于是我们对它/i*(i-1)
//由于我们的筛法可以保证我们遍历到所有的素数,于是我们可以保证j对所有的素因子做过上面的操作
//对所有的素数都进行上面的操作,得到的即是欧拉函数的值了
for (int i=2;i<=n;i++) if (!phi[i]) for (int j=i;j<=n;j+=i){
if (!phi[j]) phi[j]=j; phi[j]=ph[i][j]/i*(i-1);
}
}
10-7 交表 (UVA 10820)
有一道比赛题目,输入两个正整数x,y(1<=x,y<=n),输出某个函数f(x,y)。有位选手想交表(即事先计算出所有的f(x,y),写在源代码里),但是表太大了,源代码超过了比赛的限制,需要精简一下。
好在那道题目有一个性质,使得很容易根据f(x,y)算出f(x*k,y*k)(其中k是任意正整数),这样就有一些f(x,y)就不需要存在表里了。
输入n,你的任务是统计最简的表里有多少个元素。
分析:根据题面我们可以比较简单的得到一个结论:有必要存在表中的元素对(x,y)一定满足x与y互素,设满足x<y的二元组有T个,那么答案就是2T+1,于是问题转化为求T的值。
对于一个固定的y,即相当于求1-y中与y互素的数的个数,于是这个问题有可以转化为:phi(2)+phi(3)······+phi(n),代码如上,不再做多赘述。
10.2.3 编码与解码
概念就直接看百度吧:
编码是信息从一种形式或格式转换为另一种形式的过程也称为计算机编程语言的代码简称编码。用预先规定的方法将文字、数字或其它对象编成数码,或将信息、数据转换成规定的电脉冲信号。编码在电子计算机、电视、遥控和通讯等方面广泛使用。编码是信息从一种形式或格式转换为另一种形式的过程。解码,是编码的逆过程。
“给物体一个编号”称为编码,同理也有“解码”,即根据序号构造出物体。至于编码和解码的过程根据不同的题目的要求也有不同的处理方法。
10-8 密码 (UVA 1262)
给两个6行5列的字母矩阵,找出满足如下条件的密码:密码中的每个字母在两个矩阵的对应列中均出现。
可能会出现多个满足要求的密码,你的任务是找到字典序第k小的密码,如果不存在则输出“NO”。
分析:我们以书上举的例子为例,书上是以下两个字母矩阵:
AYGSU CBOPT
DOMRA DOSBG
XBODG APMMS
WDYPK WSXNU
PRXWO EFGHI
事实上我们可以一列一列的进行遍历,确定出第i个字母可能的情况。例如第三个字母,就只能是{G,M,O,X}。也就是说每一个位置的字母,都有若干种可能,且不同位置字母的选择不互相影响。
那么问题的处理方案就比较清晰了,具体的解决方案有两种,第一种是计算像之前全排列那里的做法一样计算每一位后面可能出现的情况,我把代码给大家拿过来给大家回顾一下:
void init_lookup_table(){fact[0]=1; for (int i=1;i<9;i++) fact[i]=fact[i-1]*i;}
//我们这里粗略看一下全排列,0-8的全排列的第一个数显然是012345678
//我们现在假设这个数是327801465
//比起012345678,在对应的序号上就多了以0,1,2这三个位为首的全排列,还有以3为首的部分排列
//以0,1,2为首的全排列个数显然为8!,也就是序号上需要加3*8!
//以3为首的部分排列的数量,我们则需要向后面看第二位
//那为什么不直接乘以当前位的值呢?因为我们所记的排列个数是除去前面已用数字的全排列个数
int try_to_insert(int s){ int code=0;//code表示排列对应的0-362879里的数值
for (int i=0;i<9;i++){
int cnt=0;
for (int j=i+1;j<9;j++) if (st[s][j]<st[s][i]) cnt++; code+=fact[8-i]*cnt;
}
if (vis[code]) return 0; return vis[code]=1;
}
不过介于这里k的最大值不超过7777,于是直接用字典序的大小一个一个枚举也是可行的。
10.2.4 离散概率初步
就是排列组合·······直接看问题吧。
抛硬币问题
连续抛三次硬币,恰好有两次正面的概率是多少?
分析:我们用1表示正面,0表示反面,110,101,011,简单枚举一下就可以了·······,答案是3/8。
条件概率
P(A|B)=P(AB)|P(B),其中P(A|B)表示在事情B发生的前提下,事情A发生的概率,P(AB)表示事件AB同时发生的概率。
贝叶斯公式:P(A|B)=P(B|A)*P(A)/P(B)
全概率公式
计算概率的一种常见方法是:样本空间S分成若干个不相交的部分B1,B2·····Bn的一个划分,则有:
P(A)=P(A|B1)*P(B1)+P(A|B2)*P(B2)+······P(A|Bn)*P(Bn)。
事实上这是一个很简单的公式,例如:参加比赛,得一等奖,二等奖,三等奖和优胜奖得概率分别是0.1,0.2,0.3,0.4,这四种情况下,你会被妈妈表扬的概率分别是1.0,0.8,0.5和0.1,则你被妈妈表扬得总概率为:0.1*0.8+0.2*0.8+0.3*0.5+0.4*0.1
10-9 决斗 (UVA 1636)
首先在手枪里随机装一些子弹,然后抠了一枪,发现没有子弹。你希望下一轮也没有子弹,是应该直接再抠一枪,还是随即转一下再扣,如果两种策略下没有子弹得概率相等,输出EQUAL。
手枪里得子弹可以看成一个环形序列,开枪一次以后对准下一个位置。例如,子弹序列为0011时,第一次开枪前一定在位置1或2(因为第一枪没有子弹),因此开枪之后位于位置2或3。如果此时开枪,有一半的概率没有子弹。
分析:简单的数学问题,直接抠一枪没子弹的概率,等于子串00的个数除以00和01总数(也就是0的个数),转一下再抠也没子弹的概率等于0的比率。
设子串00的个数为a,0的个数为b,那么两个概率分别为a/b和b/n,于是问题就转化为比较an和b2。
奶牛和轿车 (UVA 10491)
题面······看不懂(可能我高中时期就是我语文理解能力的巅峰了吧······)。
条件概率 (UVA 11181)
有n个人准备去超市逛,其中第i个人买东西的概率时Pi。逛完以后你得知,有r个人买了东西。根据这一信息,计算每个人实际买了东西的概率。
分析:“r个人买了东西”这个时间叫E,“第i个人买东西”这个事件为Ei,于是问题转化为:P(Ei|E)=P(EiE)|P(E)。
P(E)的情况用递归可以进行枚举,P(EiE)只需要同时满足E和Ei的情况,即确定第i个人一定买了东西。换个思路事实上就表示其他n-1个人中有r-1个人买了东西。
P(E)和P(EiE)的关系是不是很眼熟?是的,就是我们上一章学习的动态规划。
10-12 纸牌游戏 (UVA 1637)
36张牌分为9堆,每堆4张牌。每次可以拿走某两堆顶部的牌,但需要点数相同,如果有多种拿法则等概率的随机拿。
如果拿完则算游戏成功,求成功概率。
分析:这道题emmm,事实上我不知道和数学有什么关系,书上是说用动态规划的方法去做,用9元组表示当前状态,即每堆牌剩的张数,状态总数为59=1953125(一个可接受的数字)。设d[i]表示某9元组对应的编码i的成功概率,进行动态规划。
但事实上我觉得这道题还可以用dfs的方法直接去做:
每层dfs都有9个参数,代表每堆的数量。在每层dfs直接双重循环枚举去找两堆最高层是同等级的情况,去除掉堆顶的牌向下dfs,dfs结束的标志即是9个参数全为0或者找不到某两队最高层同等级的情况。
那么怎么求成功概率呢?事实上无论最终是否完成游戏,我们都能通过决策得到一条路径,但当且仅当路径的长度为18时,才表示游戏成功(也就是return1,否则return 0)。每一个结点的决策我们是在若干个分支点中进行选择的,例如dfs(2,3,3,2,1,1,4,3,3)到dfs(2,2,2,2,1,1,4,3,3),假设我们在dfs(2,3,3,2,1,1,4,3,3)处有sum个可能的选择,那么dfs(2,3,3,2,1,1,4,3,3)=1/sum*dfs(2,2,2,2,1,1,4,3,3)(状态转移,事实上和前面方法的状态转移方程是一样的)。
事实上可以看出两个方法的本质是一样的(不过都需要记得记忆化搜索,否则会time error)