
?递归实现:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
preOrder(root,res);
return res;
}
private void preOrder(TreeNode node,List<Integer> res){
if(node == null) return ;
res.add(node.val);
preOrder(node.left,res);
preOrder(node.right,res);
}
}非递归实现
// 利用栈实现二叉树的前序遍历
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
if(node==null) continue;
res.add(node.val);
stack.push(node.right); // 栈是先进后出,所以先压入右子树
stack.push(node.left);
}
return res;后续遍历:
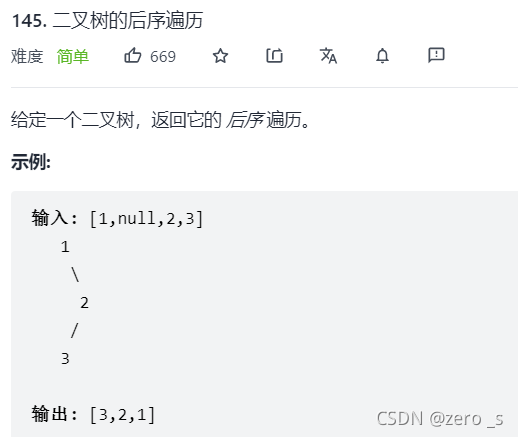
?递归实现:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postOrder(root,res);
return res;
}
private void postOrder(TreeNode node,List<Integer> res){
if(node == null) return ;
postOrder(node.left,res);
postOrder(node.right,res);
res.add(node.val);
}
}非递归的栈实现:
// 利用栈的非递归实现,利用反转的方法,左右根----> 根 右 左
List<Integer> res = new ArrayList<>();
Stack<Integer> Stack = new Stack<>();
Stack.put(root);
while(!Stack.isEmpty()){
TreeNode node = Stack.pop();
if(node == null ) return ;
res.add(node.val);
Stack.push(node.left); // 由于栈是先进后出,所以先压入左
Stack.push(node.right);
}
Collections.reverse(res);
return res;中序遍历:

?递归实现:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inOrder(root,res);
return res;
}
private void inOrder(TreeNode node,List<Integer> res){
if(node == null) return ;
inOrder(node.left,res);
res.add(node.val);
inOrder(node.right,res);
}
}// 非递归实现
List<Integer> res =new ArrayList<>();
if(root == null) return res;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root; // 给定一个指针标记根节点
while(cur != null || !stack.isEmpty()){
// 如果存在左子树保证栈顶放的是左子树节点
while(cur != null){
stack.push(cur);
cur = cur.left;
}
TreeNode node= stack.pop();
res.add(node.val);
cur = node.right;
}
return res;?
class Solution {
public int kthSmallest(TreeNode root, int k) {
// 中续遍历
List<Integer> res = new ArrayList<>();
InOrder(root,res);
return res.get(k-1);
}
private void InOrder(TreeNode root,List<Integer> res){
if(root==null) return ;
InOrder(root.left,res);
res.add(root.val);
InOrder(root.right,res);
}
}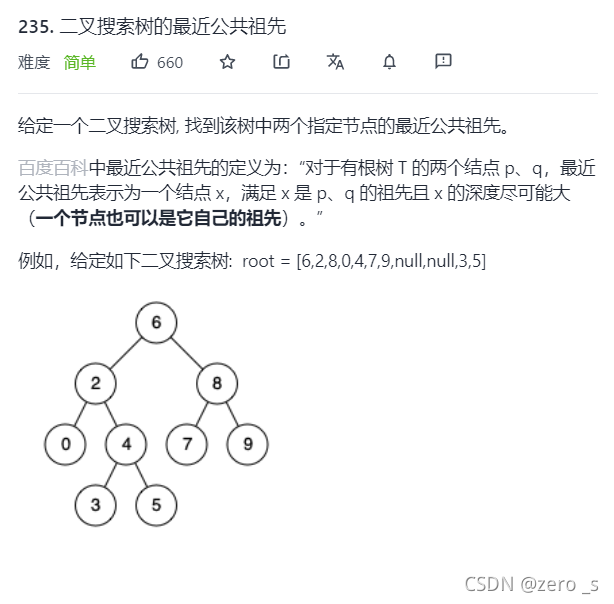
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 三种情况,如果当前根节点在p q 之间,说明当前root就是答案
// 如果root 大于pq ,说明结果在左子树上
// 如果root 小于pq,说明结果在右子树上
if(root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left,p,q);
if(root.val <p.val && root.val < q.val) return lowestCommonAncestor(root.right,p,q);
return root;
}
}?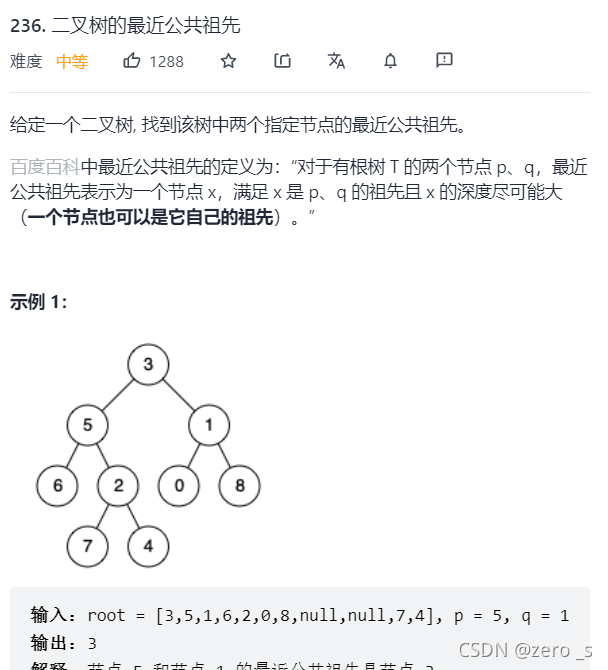
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 此时是二叉树而不是二叉搜索树
if(root==null || root ==p || root == q) return root;
// 还没找到就dfs左右子树
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
return left == null ? right : right==null ? left :root;
}
}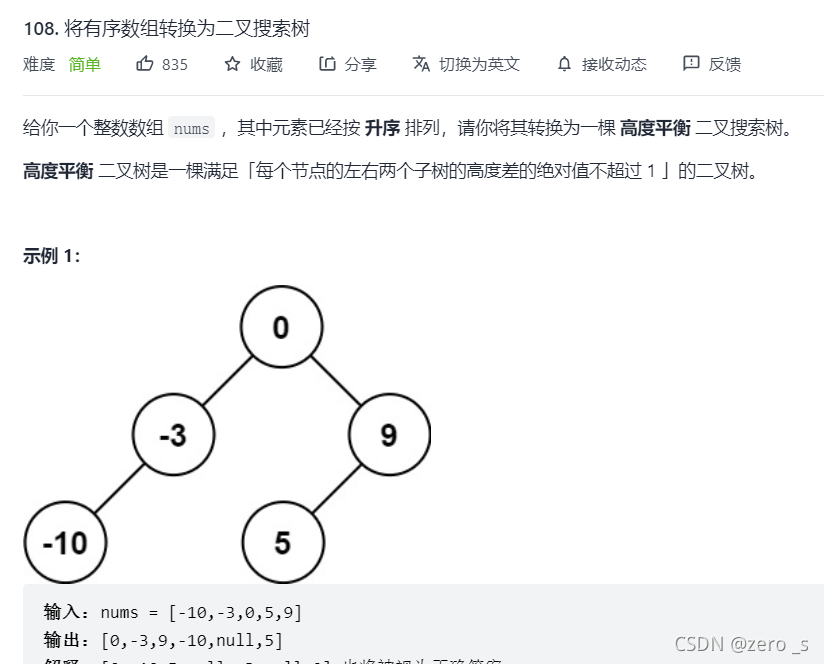
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
// 二叉搜索树的中序遍历就是一个nums数组
//所以可以让当前的中间节点作为根节点,然后递归向下拆分
return nums==null ? null: buildTree(nums,0,nums.length-1);
}
private TreeNode buildTree(int[] nums,int l,int h){
if(l>h) return null;
int mid = (l+h)/2;
TreeNode root = new TreeNode(nums[mid]);
root.left = buildTree(nums,l,mid-1);
root.right = buildTree(nums,mid+1,h);
return root;
}
}一般涉及链表元素修改的类型,而且需要一趟就达到目的,用快慢指针法。
