前言:
(温馨提示:)本文字数比较多需要慢慢观看,建议收藏此文有时间慢慢观看,看完此文你会学习到什么是链表,什么是双向链表,单链表的增删查改的基本代码思路和在线OJ题的基本代码思路。

链表的概念及结构
链表是一种物理存储结构上非连续存储结构,数据元素的逻辑顺序是通过链表中的引用链接次序实现的。
什么意思呢?
我们都知道顺序表是一组数组,在逻辑上,物理上都是连续的
但是链表在逻辑上是连续的,但是在 物理上不一定连续(内存可能连续,可能不连续)
像发哥的金链子一样,后面接着前面串起来。

实际中链表的结构非常多样,以下情况组合起来就有8种链表结构:
- 单向、双向
- 带头、不带头
- 循环、非循环
虽然有这么多的链表的结构,但是我们重点掌握两种:
-
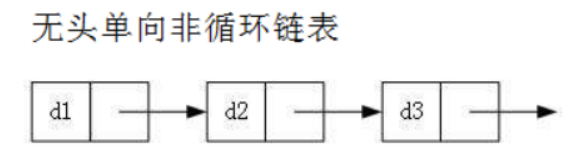
无头单向非循环链表:结构简单,一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构,如 哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
-
无头双向链表:在Java的集合框架库中LinkedList底层实现就是无头双向循环链表

来使用人话说一下什么是链表吧:

大家都吃过糖葫芦,葫芦都是一个接着一个的,长下面这样

那链表呢?
链表是由一个一个 节点构成的 ,每一个节点有两个域一个叫做数值域,一个叫做next域
data:数值域 里面存储的是数据
next:引用变量 - 存下一个节点的地址
上面的话用下面的图来展示:

从上图发现当前节点的next域存放的都是下一个节点的地址
那么最后那个没有存放下一个的地址叫做什么呢?
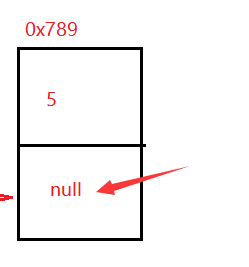
其实这个叫做尾巴节点:当这个next节点域为null的时候
有尾巴节点还会有头节点:整个链表当中的第一个节点叫做头节点
我们刚刚写的下面这个就是 不带头非循环的单链表

那么就有人会说了,你刚刚还说上面的这个是头结点啊!!!,怎么说不是带头的呢?? 请听我慢慢道来:

区分带头不带头,我给你画个图就知道了:

红色的那个就是头节点:它里面可以存放一个无效的data。
带头:其实就是标识当前链表的头
- 如果不带头:这个链表的头节点,在随时发生改变,
- 如果带头:这个链表的头节点不会发生改变。
啥是单向?? 往一个方向走就是单向
下图为:单向带头非循环

什么是循环的:最后一个节点的next域引用 第一个节点的地址 ,必须是第一个,不可以是第二个,不然不叫循环了
单向 不带头 循环 【下面的图】

单链表的实现
上面知道了链表大概是什么意思,现在我们准备使用代码来实现一下:
我们把整链表抽象为一个类:

把节点抽象为一个类:这个类里面包含data 字段 和next字段

代码如下:(为了方便 这些类就写到一个class文件里面)
先抽象出来节点类:

下面是解释:
为什么要给data搞个构造方法,因为如果不设置,那么我们不知道节点的next域要存什么地址,为什么不给next赋值呢? 因为next 是一个引用类型,默认是null,这就是我们的节点类 。

而且当我们实例化对象也发方便:
Node node = new Node(5);


在抽象出来整个链表的类:
对于链表,我们还需要一个属性 head,
这东西是一个引用,指向当前链表的头
因为当前是不带头的,头一直发生改变
要一个来一直标识单链表的头结点

接下来我要使用一种穷举的方式创建一个链表,为什么说这句话, 我怕你们说我low
代码如下:创建一个链表

上面代码什么意思呢?看我慢慢道来:
我们知道链表是 当前节点后面跟着一个节点
node1.next = node2;

可以看见node2的地址是0x456 ,所以为了成为链表node1的next要被node2赋值,这样才是一个链表。
node2.next = node3; 原理也是一样,只不过是我们的node3 没有引用,因为它是最后一个节点,后面没有下一个节点了,而且它是引用类型默认就是null了,所以不需要写node3的代码。
this.head = node1;
目前的头是node1 ,使用head指向node1所指的对象,13就是head

MyLinkedList 全部代码:
//节点类
class Node{
public int data; //数据域
public Node next; //引用类型
public Node(int data){
this.data = data;
}
}
//链表
public class MyLinkedList {
public Node head; //标识单链表的头节点
//穷举的方式创建链表 当然有点low ,此处为了好理解
public void createList(){ //创建链表
Node node1 = new Node(13);
Node node2 = new Node(2);
Node node3 = new Node(5);
node1.next =node2;
node2.next =node3;
this.head = node1;
}
}
一、实现链表的函数操作
1、实现链表的打印函数
如果head不等于null,那么就打印数据,然后让当前head,等于下一个head.next
public void show(){ //打印链表
while(this.head!=null){
System.out.print(this.head.data+" ");
this.head=this.head.next;
}
}
那为什么不可以head.next !=null
因为head.next 等于空那么最后一个数据就没有打印出来了
不过由此可以推出:
如果把整个链表 遍历完成 那么head==null
如果只是想找到链表最后一个节点 那么head.next==null
但是大家发现一个问题了没,就是head一直在动,那么head又没有意义了,不是头节点,所以要一个小弟来代替它,我们把代码优化一下,定义了一个小弟:

这就是比较完善的代码了
2、实现得到单链表的长度函数
原理很简单让cur一直遍历,如果cur不等于空 ,count++就好啦
public int size(){ //求Node 长度
Node cur =this.head;
int count =0 ;
while(cur!=null){
count++;
cur=cur.next;
}
return count;
}
3、查找是否包含关键字key是否在单链表当中
原理很简单让cur一直遍历,如果cur的data 等key 就return true
public boolean contains(int key){//查找是否包含关键字key是否在单链表当中
Node cur= this.head;
while (cur!=null){
if (cur.data == key){
return true;
}
cur = cur.next;
}
return false;
}
4、链表头插法
什么叫做头插法:
一个新节点,要插到第一个节点前面:把14这个节点插到最前面去,next是下一个结点的地址。head 要改变成为新的node

上面所说可以将代码这样写:
node.next =head;
head = node;
这样第一个14的next域就是下一个元素了
然后在把head引用node;
但是我们不可以
head = node;
node.next =head;
把他们顺序颠倒
这样变成自己引用自己了: 所以在插入一个节点的时候,一定要先绑后面
还有一个情况就是head是null,当前链表没有任何结点,插入的是第一个节点
那么代码直接: head = node;
public void addFirst(int data){
Node node = new Node(data);
node.next = this.head;
this.head = node;
}
可以使用头插法加数据,不需要使用以前的穷举了
因为是头插法最后一个后插入到第一个去,所以打印是 5 3 1

5、链表尾插法
什么叫做尾插法:
一个新节点,要插到最后节点后面:
逻辑实现:找到最后一个节点,然后把最后节点的next域变成新节点的地址,在上面我们说过,想找最后一个节点,只需要判断head.next == null,就是尾节点了
代码的实现:
public void addLast(int data){ //尾插法
Node node = new Node(data); //新节点
if (this.head ==null){ //如果是head是null 那么是第一次 直接 head = node
this.head = node;
}else{
Node cur = this.head; //定义一个cur 代替当做head
while (cur.next!=null){ //找到最后一个节点
cur = cur.next; //如果不是最后节点 一直往后走
}
cur.next =node; //当前节点的next 域指向 新节点
}
}
6、任意位置插入,第一个数据节点为0号下标
什么意思呢? 我们需要把新的节点 插入目标节点的后面(下面的红色是新节点)

具体实现思路:
如果想实现变成链表,我们必须得把 当前节点的next域 变成 后面一个节点的地址
然后把前一个的next域 变成 新节点的地址,这就是 核心思路!!
我们先把代码放出来,依次解析:
public Node searchPrev(int index){
Node cur = this.head;
int count = 0;
while (count != index -1){ //给个条件 找到前一个就退出
cur = cur.next; //继续找的条件
count++;
}
return cur; // 返回前面的一个
}
public void addIndex(int index , int data){ //任意位置插入,第一个数据节点为0号下标
if(index<0 || index >size() ){ //判断需要放入的位置是否合法
System.out.println("下标不合法");
return;
}
//头插法
if(index == 0){
addFirst(data);
}
//尾插法
if (index ==size()){
addLast(data);
}
Node cur= searchPrev(index);
//新节点的插入 核心代码
Node node = new Node(data);
node.next = cur.next;
cur.next =node;
}
大家可以看见上面有 两个方法,我们先来看一下searchPrev() 这个函数
searchPrev(): 找到需要插入的前一个节点的方法;
为什么需要这个方法呢?
因为我们的这个链表不是循环的链表,如果我们找到的不是插入的前一个节点,那么我们就不知道前一个节点的next域是多少,因此不成立链表的实现,所以不可以。
好了现在来解析一下这个searchPrev()函数:
public Node searchPrev(int index){ //需要插入的下标
Node cur = this.head; //定义一个cur 代替head
int count = 0; //计数
while (count != index -1){
//给个条件 count不等于index-1 就进入,换句话说就是找到index-1 就退出
cur = cur.next; //继续找的条件
count++;
}
//退出了 当前cur就是 index -1
return cur; // 返回前面的一个
}
以上就是这个函数的意思,那我们看看下一个函数addIndex();
public void addIndex(int index , int data){ //任意位置插入,第一个数据节点为0号下标
if(index<0 || index >size() ){ //判断需要放入的位置是否合法
System.out.println("下标不合法");
return;
}
//头插法
if(index == 0){ //如果index等于0 就是头插法
addFirst(data);
}
//尾插法
if (index ==size()){ //size是个函数 上面写过,
//如果index等于size 就是全部长度,也就是尾插法
addLast(data);
}
Node cur= searchPrev(index); //前一个节点
//新节点的插入 核心代码
Node node = new Node(data); //这个是新节点
//核心代码
node.next = cur.next;
cur.next =node;
}
怎么理解核心代码呢?
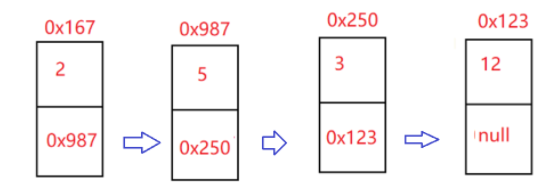
看下面的图:可以看出 现在cur的next 等于node2

那么 node.next = cur.next; 这个代码的意思就是把 0x789给了新节点

就意味着是新节点 指向刚刚那个0x789 node2

那么竟然新节点已经指向node2 那 cur 是不是应该指向 新节点呢?
所以 cur.next =node;

所以这才是一个完美的链表插入!!!
7、删除指定的节点
删除结点原理就是让那个节点不被引用,这样就会被JVM自动回收(当没有被引用时会被自动回收),我们可以让被删除的节点不被引用,让被删除前面的节点引用被删除后面的那个节点,这样删除的节点在中间没有被引用就会自己被回收,达到删除的效果。

代码送上:
public Node searchPrevNode(int val){
Node cur = this.head;
while (cur.next!=null){
if (cur.next.data==val){
return cur;
}
cur = cur.next;
}
return null;
}
public void remove(int val){ //删除第一次出现的关键字为key的节点
if (this.head == null){
return;
}
if (this.head.data==val){
this.head =this.head.next;
return;
}
Node cur = searchPrevNode(val);
if (cur==null){
System.out.println("没有要删除的节点");
return;
}
Node del = cur.next;
cur.next =del.next;
}
让我们依次解析:searchPrevNode();
public Node searchPrevNode(int val){
Node cur = this.head; //定义一个head
while (cur.next!=null){//循环节点
if (cur.next.data==val){
//如果下一个结点的值 等于要删除的值 那么就返回前一个值
return cur;
}
cur = cur.next; //让条件继续
}
return null; //找不到返回null
}
上面代码核心是: 为什么要找到前面的节点?
if (cur.next.data==val){
//如果下一个结点的值 等于要删除的值 那么就返回前一个值
return cur;
}
上面我们说过,找到要删除结点的 前面节点,让前面的节点不要引用被删除的节点,就可以达到删除的效果
解析:remove()
public void remove(int val){ //删除第一次出现的关键字为key的节点
if (this.head == null){ //如果没有节点要删除
return;
}
if (this.head.data==val){ //如果删除第一个结点
this.head =this.head.next; //让当前结点被下一个节点引用
return;
}
Node cur = searchPrevNode(val);
if (cur==null){ //上面函数可能返回null
System.out.println("没有要删除的节点");
return;
}
Node del = cur.next; //被删除节点 就是cur的next域
cur.next =del.next; //让cur的next等于del.next
//del.next 是要删除的节点下一个地址
}
来看看较难理解的代码:
if (this.head.data==val){ //如果删除第一个结点
this.head =this.head.next; //让当前结点被下一个节点引用
return;
}

head.next == 0x456 ,所以head指向0x456
二:
Node del = cur.next; //被删除节点 就是cur的next域
cur.next =del.next; //让cur的next等于del.next
//del.next 是要删除的节点下一个地址

8、删除全部指定的节点
删除全部指定的结点也是和删除差不多一样的原理,把要删除的那个节点不被引用即可:
比如下面要删除 【2】 这个结点:下面的做法就是让prev的next域等于 cur的next域,这样prev的next域,就没有引用cur ,而是引用cur.next域(就是【5】这个节点)

public void removeAllKey(int key){ //删除给定的所有值
if(this.head==null)return; //判断如果head是空 证明没有节点,直接return
Node prev = this.head; //定义一个前驱 方便操作
Node cur = this.head.next; //定义一个cur 从第二个节点开始
while (cur!=null){ //条件是cur不等于空 就进去执行代码
if(cur.data == key){ //如果当前cur等于要删除的
prev.next=cur.next; //把前驱的引用指向第二个节点的next域(也就是cur的下一个结点)
cur = cur.next; //cur往后走一步
}else{ //如果不是要删除的节点
prev=cur; //让前驱等于下一个
cur = cur.next; //让cur等于下一个
}
}
if (this.head.data==key){ //最后判断第一个是不是要删除的节点
this.head = this.head.next; //当前的head引用下一个
}
}
9、清空全部节点
清空节点原理很简单:就是让当前的节点的next不引用后面的域,然后依次置空即可, 当然我们可以暴力点直接head等于null,那么这样后面的节点依次就没有被引用,就会被JVM回收掉。下面这图就是介绍上面所说的:

public void clear(){//删除所有节点
while (this.head!=null){ //当不等于空进入
Node curNext = this.head.next; //把下一个地址保存
this.head.next = null; //把下一个的地址置空
this.head = curNext; //把当前节点不被引用
}
}
那么我们怎么证明已经把它给"干掉了呢"?
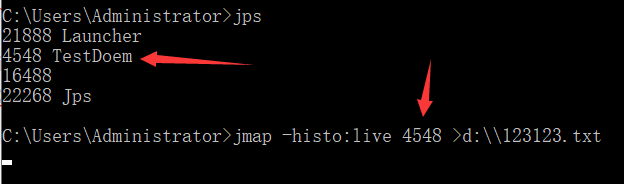
1、打个断点调试起来

2.打开cdm 输入 jps 查看当前java进程
然后输入:
jmap - histo:live 4548
(jmap是JDK自带的工具软件,主要用于打印指定Java进程(或核心文件、远程调试服务器)的共享对象内存映射或堆内存细节)
意思是:这些东西会查出很多信息,打印到你的cmd中 但是这样不方便 我们可以重新重定向一下,把查出信息放在d盘下123123.txt 文件 方便阅读
jmap -histo:live 4548>d:\123123.txt
注意图上的箭头所指向的要是一样 比如我上面是4548 live后面也是4548,然后按回车,发现它在一闪一闪,我们去idea执行下一步操作
然后去找到文件打开即可:
ctrl+f 找一下 节点 (我的节点叫做Node)这里是有4个

我的程序里面也刚刚好是4个

这个时候我们关闭程序,调用一下clear()方法,,先调研方法

然后执行上面的操作 (注意数字)

这个时候我们去文档搜索一下,发现没有第一次的node节点了

证明成功了我们!
二、链表的面试题
1.反转一个单链表。
上面这个题,很多同学会搞不清楚,会逆置数据,其实注意是错误的
正确的应该是这样的:最后一个到前面来了,引用的next域也需要改变
思路:我们可以使用头插法,先把第一个节点的next域改变成null,这样第一个节点就是最后一个节点了,然后想办法让后面节点的next域等于前面的节点,也就是相当等于反过来了。

public Node reverseList() { //反转一个单链表
if(head==null) return null; //如果没有返回null
if(head.next==null) return head; //如果就一个 返回这个一个节点
Node cur = this.head; //定义一个头
Node prev = null; //前驱为空(为了让第一个节点变成最后一个节点 )
while(cur!=null){ //遍历
Node curNext = cur.next; //因为要替换前一个节点 所以要保留后面的节点
cur.next = prev; //第一个的节点next域为null 变成最后一个
prev = cur; //前驱等于当前节点
cur = curNext; //当前节点去下一个节点
}
return prev; //返回最头的节点
}
打印的话 函数也得变一下,要从新的头打印 不可使用以前的函数
/从指定位置开始打印
public void show2(Node newHead){
Node cur = newHead;
while(cur != null){
System.out.print(cur.data+" ");
cur=cur.next;
}
}
2.返回中间节点,有2个返回第二个中间的节点


思路:使用快慢指针fast走2步,slow走1步,当fast等于null那么是4个节点,fast.next等于null 那么是5个节点

public Node middleNode() {
if(head==null) return head; //当头节点等于空 返回null
Node fast = head; //快指针 在头部
Node slow =head; //慢指针 在头部
while(fast!=null && fast.next!=null){ //往前走的条件
fast = fast.next.next; //快的走2步
slow = slow.next; //慢的走一步
}
return slow; //慢的肯定在中间
}
3.输入一个链表,输出该链表中倒数第k个结点。
原理很简单 :快慢指针即可 ,先快指针走k-1步,然后慢指针一起走,为什么可以:假设找倒数第二个节点 fast先走 k-1步(也就是一步),然后一起走,当fast.next等于null 返回slow

为什么呢? 比如我们跑步你一直差我k-1的距离,等我到了你是不是还差k-1的距离, 假如你要找倒数第3个格子,你比我差2格,对于节点来说,是不是意味着到了终点,后面还有2个格子,加上终点的格子 一共有3个,所以就是这个原理
public Node findKthToTail(int k) { //倒数第k个节点
if(head==null) return null; //如果的是第一个节点是null 返回null
if(k < 0){ //k不可以小于0 不然是负数
return null; //返回是null
}
Node fast = head; //快指针
Node slow = head; //慢指针
while(k-1 !=0){ //让快指针先走 k-1步
if(fast.next!=null){ //如果条件不成立 证明k大于我们的节点长度
fast = fast.next;
k--;
}else{
return null;
}
}
while(fast.next != null){ // 然后一起走
fast = fast.next;
slow = slow.next;
}
return slow;
}
4.合并两个有序链表。

原理:定义一个新无用的节点,然后让链表A 和链表B的值去比较,谁小就放在无用节的next域,每放好一次链表向后走,傀儡结点引用傀儡节点的next域,往后面走,然后在循环拿新值去比较,最后当链表A为空,就然傀儡节点的next等于链表B(前面全部引用完了,后面的可以直接等于链表B 因为链表B本身就是一个有序的),反之一样 ,最后返回傀儡节点的next,因为next域是第一个节点
public Node mergeTwoLists(Node headA, Node headB) { //合并有序的节点
if(headA==null)return headB; //如果headA是空返回headB
if(headB==null)return headA;
if(headA==null && headB ==null)return null; //全部null返回null
Node newHead = new Node(-1); //定义傀儡节点(无用节点)
Node tmp = newHead; //定义一个标记 引用下一个节点地址
while(headA!=null && headB!=null){ //条件
if(headA.data< headB.data){ //比较他们的值大小
tmp.next = headA; //傀儡节点的下一个是headA
headA = headA.next; //让headA在往后去一个节点
}else{
tmp.next = headB;
headB = headB.next;
}
tmp = tmp.next; //假设傀儡节点已经是1 后面是其他数字, 应该要去下一个节点,继续引用其他的
}
if(headA==null){ //如果链表A 全部跑完了
tmp.next = headB; //傀儡节点 只直接引用headB的全部
}
if(headB==null){
tmp.next = headA;
}
return newHead.next; //返回的是傀儡节点的下一个域 因为当前节点是没有用的
}
5.以给定值x为基准将链表分割成两部分,所有小于x的结点排在大于或等于x的结点之前
什么意思呢?如果给了个x=4;链表比4小的一边,比4大的在一边,而且以前的顺序不可以改变

代码思路:和x值比较如果大于等于X的放一边,反之放另外一边,怎么取分边界呢,我们可以定义4个引用,bs be,as se, s是开始,e是结尾,最后排序好在让next等于下一个的头。

public Node partition(ListNode pHead , int x) {
// write code here
// write code here
Node cur = pHead ; //定义一个代替头
Node bs = null; //小于x的bstar 开始的头节点
Node be = null; //小于x的bend 结束的尾节点
Node as = null;
Node ae = null;
while(cur!=null){ //遍历cur
if(cur.data<x){ //如果当前的data大于 x
if(bs==null){ //判断是不是为空
bs = cur; //头尾都是开始
be = cur; //头尾都是开始
}else{
be.next = cur; //尾插法
be = be.next; //尾往后走
}
}else{
if(as==null){
as = cur;
ae = cur;
}else{
ae.next =cur;
ae = ae.next;
}
}
cur = cur.next; //cur 往后走
}
if(bs==null){ //如果第一段头是空
return as; //返回下一段的头节点
}
be.next = as ; //第一段的尾巴 链接第二段的头
if(as!=null){ //第二段的头不等于空
ae.next = null; //第二段(也就是最后的尾等于空)
}
return bs ; //返回第一段的头
}
6.在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。

代码思路:定义一个傀儡节点,最后返回傀儡节点的next域,当前的节点的val值和下一个对比 是否是一样的,如果是一样的则跳过,如果不是一样的,那么傀儡节点的next等于它,依次循环。 最后的节点next域等于null;、

public ListNode deleteDuplication(ListNode pHead) {
ListNode newHead = new ListNode(-1); //定义一个头节点
ListNode tmp = newHead; //傀儡节点
ListNode cur = pHead; //当前头
while(cur!=null){ //cur 不等于空
if(cur.next!=null && cur.val == cur.next.val){ //cur在走的过程中有可能是相同的
while(cur.next!=null && cur.val == cur.next.val){
cur = cur.next;
}//走到相同的最后一个
cur = cur.next; //在走一个就不是相同的
}else{ //如果不是相同的
tmp.next = cur; //傀儡节点的next等于下一个
tmp = tmp.next; //傀儡节点往后走
cur = cur.next; //cur往后走
}
}
tmp.next = null; //最后的节点的next域等于空
return newHead.next; //返回傀儡节点
}
7.链表的回文结构。
代码思路: 判断回文 我们可以先找中间结点,然后翻转,依次判断是否是回文

public boolean chkPalindrome(ListNode head) {
// write code here
if (head ==null){ //判断有没有节点
return true;
}
if (head.next ==null){ //只有一个节点的情况
return true;
}
//找中间节点 定义快慢指针
ListNode fast = head;
ListNode slow = head;
while(fast!= null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
}
//进行翻转
ListNode cur = slow.next;
while (cur!= null){
ListNode curNext = cur.next;
cur.next = slow;
slow = cur;
cur = curNext;
}
//判断回文
while (slow!= head){
if (slow.val != head.val){
return false;
}
if (head.next ==slow){ //如果是偶数
return true;
}
slow =slow.next; //个往下一步走
head = head.next;
}
return true;
}
8.给定一个链表,判断链表中是否有环。
OJ链接

代码思路:很简单判断有没有可以使用快慢指针:fast指针走两步,慢指针走一步,每次走完判断一下即可:

代码:
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(fast!=null && fast.next!=null){
fast = fast.next.next; //快的走两步
slow = slow.next; //慢的走一步
if(slow==fast){ //每次判断一下
return true;
}
}
return false;
}
9. 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null
代码原理:/两个指针,从头结点和相遇结点,各走一步,直到相遇,相遇点即为环入口

public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(fast!= null && fast.next !=null){
fast = fast.next.next;
slow = slow.next;
if(slow==fast){
break;
}
}
if(fast ==null ||fast.next ==null){
return null;
}
//找入环第一个结点
slow = head;
while(fast!=slow){
fast = fast.next;
slow = slow.next;
}
return slow;
}
10. 输入两个链表,找出它们的第一个公共结点

代码思路:既然有2个链表,我们可以让他们达到相同的位置,在让他们一起一步一步的往下走,最后他们相等则发回地址:

代码如下:
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA == null){
return null;
}
if(headB == null){
return null;
}
//求长度
int lenA = 0;
int lenB = 0;
ListNode pl= headA; //假设pl 是最长的链表
ListNode ps= headB;
while(pl!=null){
lenA++; //计算长度差值
pl = pl.next;
}
while(ps!=null){
lenB++;
ps = ps.next;
}
pl = headA ; //上面走完已经是null 我们回到原来位置
ps = headB ;
int len = lenA - lenB; //差值步
if(len<0){
pl = headB;
ps = headA;
len = lenB-lenA; //重新 不然会是负数
}
while (len!= 0 ){ //走差值步
pl = pl.next;
len--;
}
while (pl!=ps){ //一起向后走
pl = pl.next;
ps = ps.next;
}
return pl; //返回
}
三、面试经常问到的问题:
顺序表+单链表
1.数组和链表的区别
2.顺序表的和链表的区别
3.ArrayList和LinkedList的区别
对于上面的问题,我们有个技巧:从他们的共性出发。
1.怎么组织数据的?
- 对于顺序表来说,底层是一个数组组成的,对于链表来说,每个数据是由节点组织的链表来说,是由节点和节点的指向之间进行组织的。
2.增删查改
- 顺序表不适合插入和删除,(因为每次需要移动元素),但是适合查找,为什么,只要给数组一个下标,可以立马找到这个数据。
- 链表适合插入删除,每次插入删除顺序,只需要修改指向即可。
3.ArrayLinst 和LinkedList是什么:
- 这2个类是Java当中的集合类,他们就是封装好的顺序表和链表。
- 强调一点:LinkedList底层是一个双向链表!(接下来学习双向链表)

双向链表的认识:
双向链表:

和单向链表不同,双向链表多了一个prev域(前驱)
双向链表有什么用?
1.引用了前驱域,解决了单链表只能单向访问的痛点
2.对于双向链表来说,第一个节点和最后一个节点要注意:第一个节点的前驱是null,最后一个节点的后继是null
双向链表有head 和 last 保持当前节点的头节点和尾巴节点

有last的好处: 如果需要插入一个数据,我们可以直接插入在last后面即last.next==node,然后把node的前驱改成last,节省步骤。
接下来创建我们的双向链表吧:
class ListNodeD {
public int data; //数据域
public ListNodeD prev; //前驱域
public ListNodeD next; //尾巴域
public ListNodeD(int data) {
this.data = data; //构造函数给data赋值
}
}
一、实现链表的函数操作
1.双向链表的头插法
代码思路:和单链表的差不多,不过需要注意我们有了prev这个域,
核心代码:可对比下图
node.next = this.head;
this.head.prev = node;
head = node;

//头插法
public void addFirst(int data) {
ListNodeD node = new ListNodeD(data);
if(head == null){
this.head = node;
}else{
//按照上面的图来
node.next = this.head;
this.head.prev = node;
head = node;
}
}
2.双向链表的尾插法
代码思路:和单链表的差不多,不过需要注意我们有了prev这个域,

//尾插法
public void addLast(int data) {
ListNodeD node = new ListNodeD(data);
if (this.head==null){
this.last = node;
this.head = node;
}else{
last.next = node;
node.prev =last;
last =node;
}
}
3.任意位置插入,第一个数据节点为0号下标
代码思路:找到要插入的位置 不需要向单链表一样找前一个,注意插入合法性

//找位置
public ListNodeD findIndex(int index){
ListNodeD cur = this.head;
while(index!= 0){
cur =cur.next;
index--;
}
return cur;
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data) {
if (index==0){
addFirst(data);
return;
}
if (index==size()){
addLast(data);
return;
}
if(index < 0 || index>size() ){
System.out.println("index位置不合法");
return;
}else{
ListNodeD cur = findIndex(index);
ListNodeD node = new ListNodeD(data);
node.next = cur;
cur.prev.next = node;
node.prev =cur.prev;
cur.prev =node;
}
}
4.删除第一次出现关键字为key的节点
代码思路;思路很简单 就是利用好JVM回收机制,因为是双向链表我们需要考虑的域比较多,我们删除的情况也需要考虑的比较多,分为头节点删除,中间其他节点删除,和最后的尾巴节点删除,这个链表 没有什么多技巧只有多画图…

public void remove(int key) {
if(this.head==null){
return;
}
ListNodeD cur = this.head; //定义一个 cur
while (cur!=null){ //循环遍历
if (cur.data==key){ //判断是否等于要删除的
//判断是不是头节点
if(cur==this.head){ //当cur是头节点
this.head = this.head.next; //让头节点等于下一个节点
if(this.head == null){ //如果当前的头节点是null(证明只有一个节点)
this.last = null; //那么把last也给那1个节点
}else{
this.head.prev = null; //(不只一个 但是是第一个节点)把当前前驱置空
}
}else{
cur.prev.next = cur.next; //把当前的前一个节点的next 赋值为cur 的后面那个地址 这样cur 不被引用
//尾巴节点
if (cur.next == null){ //是尾巴节点 (证明是删除最后一个)
this.last = cur.prev; // 那么把前面一个给赋值变成last
}else{ //中间节点
cur.next.prev = cur.prev; //把前驱也改变为 已经被删除的前驱
}
}
return;
}else{
cur = cur.next;
}
}
}
5.删除所有值为key的节点
代码思路:可以使用上面的删除 只需要把上面的代码稍微修改修改:
public void removeAllKey(int key) {
if(this.head==null){
return;
}
ListNodeD cur = this.head; //定义一个 cur
while (cur!=null){ //循环遍历
if (cur.data==key){ //判断是否等于要删除的
//判断是不是头节点
if(cur==this.head){ //当cur是头节点
this.head = this.head.next; //让头节点等于下一个节点
if(this.head == null){ //如果当前的头节点是null(证明只有一个节点)
this.last = null; //那么把last也给那1个节点
}else{
this.head.prev = null; //(不只一个 但是是第一个节点)把当前前驱置空
}
}else{
cur.prev.next = cur.next; //把当前的前一个节点的next 赋值为cur 的后面那个地址 这样cur 不被引用
//尾巴节点
if (cur.next == null){ //是尾巴节点 (证明是删除最后一个)
this.last = cur.prev; // 那么把前面一个给赋值变成last
}else{ //中间节点
cur.next.prev = cur.prev; //把前驱也改变为 已经被删除的前驱
}
}
cur = cur.next;
}else{
cur = cur.next;
}
}
和上面的代码不一样,在这里没有呢return 出去,而是继续下去一直循环,直到cur等于null

好了以上就是基本的一些链表知识点,希望可以对你有一些帮助,喜欢此文可以收藏点赞感谢感谢!!!