一、题目描述
有 N 个网络节点,标记为 1 到 N。
给定一个列表 times,表示信号经过有向边的传递时间。 times[i] = (u, v, w),其中 u 是源节点,v 是目标节点, w 是一个信号从源节点传递到目标节点的时间。
现在,我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1。
二、理解题意
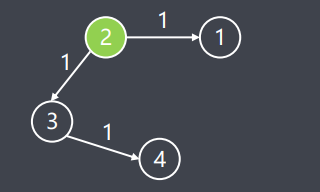
? 我们需要找到从给定节点k发出的信号多久后可以到达所有节点。
? 每条边都被赋予了长度(边权),即信号在该边传输所用的时间。
? 观察:从节点k发出的信号到达节点a的最短时间就是在图中节点k到节点a最短路径的长度。
? 题目所求的时间就是距离节点k最远的节点与节点k之间的最短距离。
三、解法一:深度优先遍历
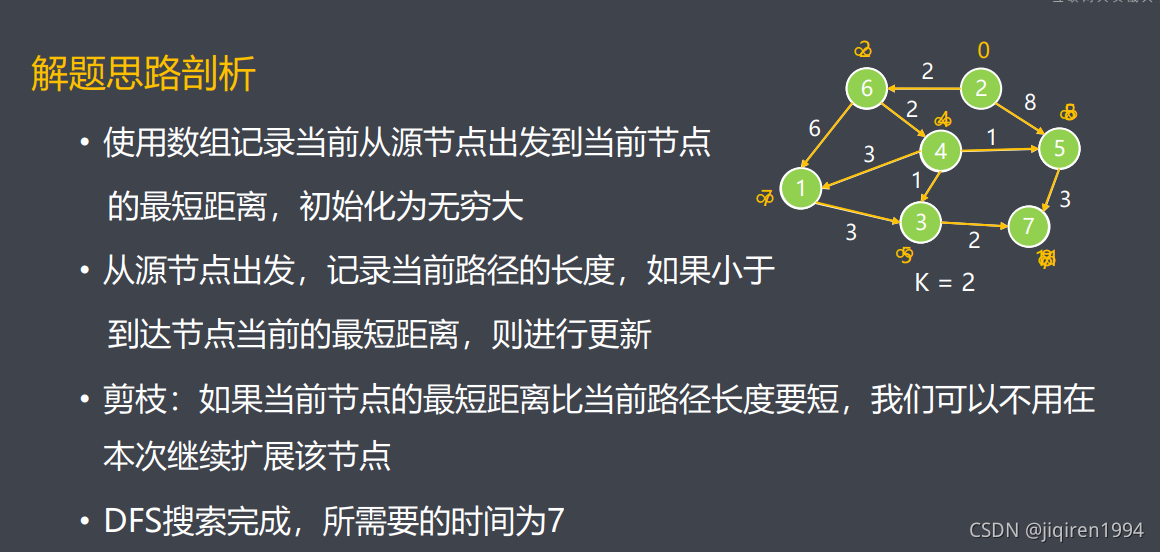

public int[] dist; //dist存储从源节点k到各个节点的最短距离
public int networkDelayTime(int[][] times, int N, int K) {
//构建有权图的邻接表adj
ArrayList<ArrayList<int[]>> adj = new ArrayList<ArrayList<int[]>>(N+1);
for(int i=0; i <= N; i++)
adj.add(new ArrayList<int[]>());
for(int i=0; i < times.length; i++)
adj.get(times[i][0]).add(new int[]{times[i][1], times[i][2]});
dist = new int[N+1];
//初始化最短距离为无穷大
for (int node = 1; node <= N; ++node)
dist[node] = Integer.MAX_VALUE;
dfs(adj, K, 0); //从起始节点K开始dfs
int ans = 0; //寻找最短路径中的最大值并返回
for (int node = 1; node <= N; ++node){
if (dist[node] == Integer.MAX_VALUE) return -1;
ans = Math.max(ans, dist[node]);
}
return ans;
}
public void dfs(ArrayList<ArrayList<int[]>> adj, int node, int elapsed) {
//剪枝:若之前存在更快到达node节点的路径,本次无需继续扩展该节点
if (elapsed >= dist[node]) return;
dist[node] = elapsed;
for(int j=0; j<adj.get(node).size(); j++){
int[] vert=adj.get(node).get(j);
dfs(adj, vert[0], elapsed + vert[1]);
}
}
解法二:迪杰斯特拉算法



public int networkDelayTime(int[][] times, int N, int K) {
//构建有权图的邻接表adj (同基本解法)
//dist存储从源节点k到各个节点的最短距离,初始化最短距离为无穷大
int[] dist = new int[N+1];
for (int node = 1; node <= N; ++node) dist[node] = Integer.MAX_VALUE;
dist[K] = 0;
boolean[] visited = new boolean[N+1]; //即集合D
while (true) {
int candNode = -1;
int candDist = Integer.MAX_VALUE;
for (int i = 1; i <= N; ++i) { //寻找下一个加入集合D的节点
if (!visited[i] && dist[i] < candDist) {
candDist = dist[i];
candNode = i;
}
}
if (candNode < 0) break; //到所有可达节点的最短路径都寻找完毕,退出循环
visited[candNode] = true;
for(int j=0; j<adj.get(candNode).size(); j++){
int[] info =adj.get(candNode).get(j);
dist[info[0]] = Math.min(dist[info[0]], dist[candNode] + info[1]);
}
}
int ans = 0; //寻找最短路径中的最大值并返回
for (int node = 1; node <= N; ++node){
if (dist[node] == Integer.MAX_VALUE) return -1;
ans = Math.max(ans, dist[node]);
}
return ans;
}
public int networkDelayTime(int[][] times, int n, int k) {
//构建有权图的邻接表adj (同基本解法)
List<ArrayList<int []>> adj=new ArrayList<>();
for(int i=0;i<n+1;i++){
adj.add(new ArrayList<>());
}
for(int [] time:times){
adj.get(time[0]).add(new int[]{time[1],time[2]});
}
//dist存储从源节点k到各个节点的最短距离,初始化最短距离为无穷大
int[] dist = new int[n+1];
for (int node = 1; node <= n; ++node) dist[node] = Integer.MAX_VALUE;
//创建最短距离的前前置节点
int[] pre= new int[n+1];
dist[k]=0;
PriorityQueue<Integer> queue=new PriorityQueue<Integer>((i1,i2)->{
//如果距离相等
return dist[i1]-dist[i2];
});
//从k开始执行遍历,设置为0,自动浮动到顶点
queue.offer(k);
while(!queue.isEmpty()){
int node= queue.poll();
//遍历节点,设置相关的distince
List<int []> ds=adj.get(node);
for(int [] nextNode:ds){
if(nextNode[1]+dist[node]<dist[nextNode[0]]){
dist[nextNode[0]]=nextNode[1]+dist[node];
pre[nextNode[0]]=node;
queue.offer(nextNode[0]);
}
}
}
int ans = 0; //寻找最短路径中的最大值并返回
for (int node = 1; node <= n; ++node){
if (dist[node] == Integer.MAX_VALUE) return -1;
ans = Math.max(ans, dist[node]);
}
return ans;
}