[数据结构与算法]复习二叉树

二叉树复习

#情报学/算法

一些不熟悉的基本概念

• 结点的度（degree）：结点拥有的子树的棵数
• 叶子leaf：度为0
• 分支结点：除了叶子结点意外的结点
• 树的度：树中结点的度的最大值
• 深度为k的二叉树，至多有2^k-1个结点
• 对于任何一颗二叉树，如果其叶子结点数为N0，度为2的结点树为N2，那么N0=N2+1

总的边数为N，N=N0+N1+N2-1，因为根结点没有边，所以减去一个1 N=1xN1+2xN2，度为一的点有一条边，度为二的点有两条边
两个式子结合就得到N0=N2+1

• 满二叉树与完全二叉树的区别（最后一层从左到右有结点）

二叉树存储结构

顺序存储
略

链式存储

二叉树的遍历

先序遍历

1. 访问根结点
2. 访问左子树
3. 访问右子树
   

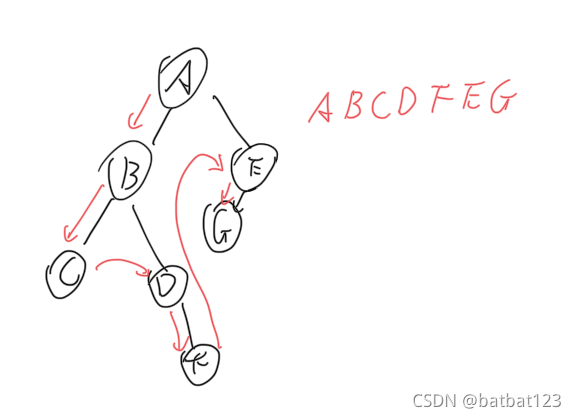
中序遍历

1. 访问左子树
2. 访问根结点
3. 访问右子树
   

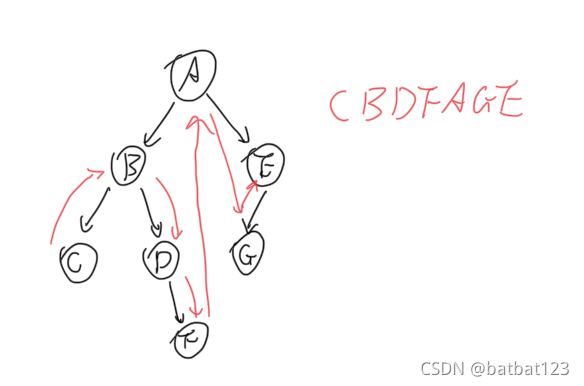
后序遍历

1. 访问左子树
2. 访问右子树
3. 访问根结点
   

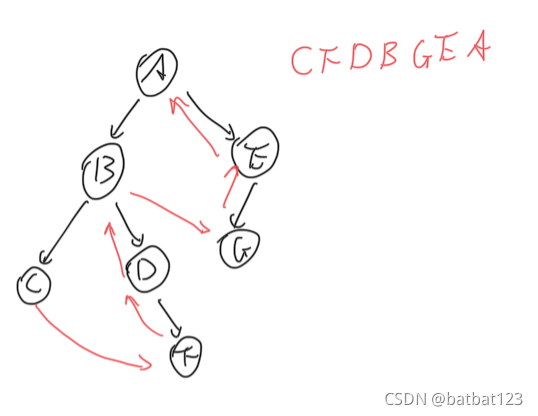
深度优先遍历和广度优先遍历

深度优先遍历：指前序遍历和后序遍历（递归，栈实现）
广度优先遍历：是分层次进行访问（非递归，队列实现）

堆

• 最小堆：父亲结点的关键码的值小于或等于子女的，根结点是全树的最小值
• 最大堆：相反

赫夫曼树

• 路径长度path length：从树中的一个结点到另一个结点之间分支构成这两个结点之间的路径长度，路径上的分支数目称作路径长度。
• 树的路径长度：树的路径长度是从树根到每一个结点的路径长度之和。
• 树的带权路径长度：树的带权路径长度为树中所有叶子结点k的带权路径长度之和，叶结点右权值的二叉树叫做扩充二叉树
  树の路径长度
  

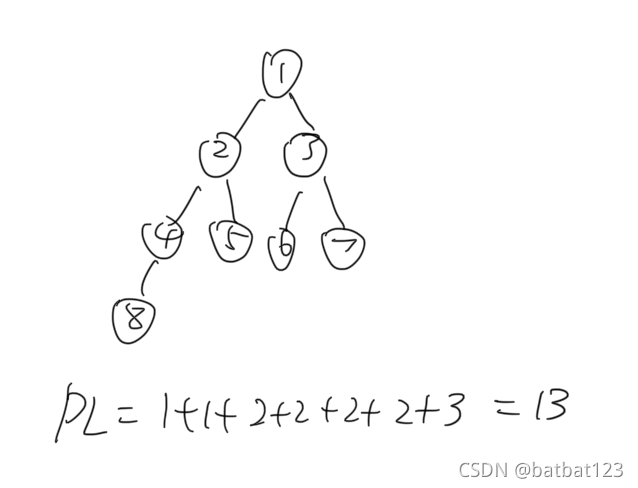
带权树

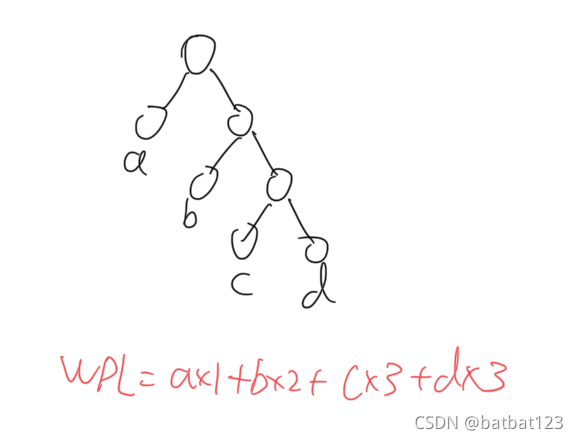
赫夫曼树：对于同一个权值集合，组成的WPL最小的树，叫做赫夫曼树

如何构建赫夫曼树

挑选出权值最小的两个，组成一个树，小的在为左子树，大的为右子树，组成的根结点权值为两者相加，然后将权值放回原来的结合中，再挑选最小的两个，重复