[数据结构与算法]堆排序算法

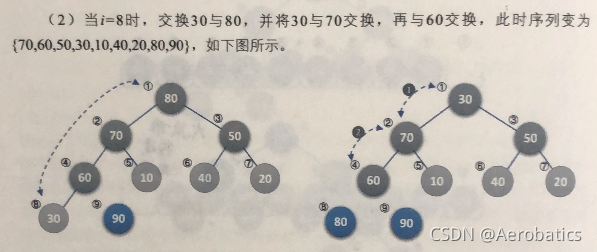
堆排序

1.大顶堆和小顶堆

堆是具有下列性质的完全二叉树：大顶堆和小顶堆的性质

大顶堆：每个结点的值大于等于其左右孩子结点的值

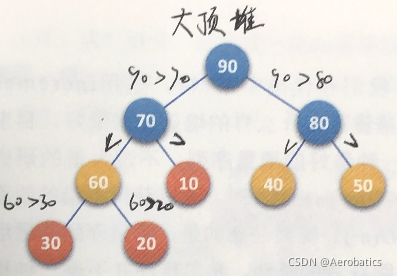
双亲结点 $k_i\ge k_{2i}$ 其左孩子结点（其中 $i$ 代表结点在数组中的下标）
双亲结点 $k_i\ge k_{2i+1}$ 其右孩子结点
1 $\le i\le$$?$ $\frac{n}{2}$ $?$ (向下取整)
对于有$n$个结点的二叉树，第$n$个结点的双亲为二叉树中第$?$ $\frac{n}{2}$ $?$个结点

小顶堆：每个结点的值小于等于其左右孩子结点的值

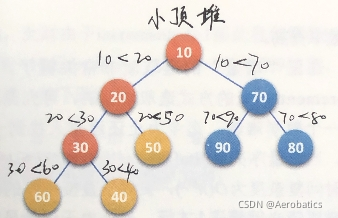
双亲结点 $k_i\le k_{2i}$ 其左孩子结点（其中 $i$ 代表结点在数组中的下标）
双亲结点 $k_i\le k_{2i+1}$ 其右孩子结点
1 $\le i\le$$?$ $\frac{n}{2}$ $?$ (向下取整)
对于有$n$个结点的二叉树，第$n$个结点的双亲为二叉树中第$?$ $\frac{n}{2}$ $?$个结点

2.堆排序算法

步骤：
1.将现在的待排序序列构建成一个大顶堆（或小顶堆）
2.逐步将每个最大值的根结点与末尾元素交换，并且再调整其成为大顶堆（或小顶堆）

堆排序算法实现

void HeapSort(SqList *L){
	for(int i=L->length/2; i>0; i--)  //构建大顶堆
		HeapAdjust(L,i,L->length);
	for(int i=L->length; i>1; i--){   //排序
		swap(L,1,i);	//交换第一个结点(最大值)和第i个结点(当前未排序的子序列的末尾元素交换)
		HeapAdjust(L,1,i-1);	//将r[1]..r[i-1]重新调整为大顶堆
	}
}

HeapAdjust具体实现

void HeapAdjust(SqList *L, int s, int m){	//调整r[s]使得r[s]...r[m]成为一个大顶堆
	int temp;
	temp=L->r[s];
	//当前结点序号s，其左孩子2s，右孩子2s+1
	//j<m说明下标为j的结点不是最后一个结点
	for(int j=2*s; j<=m; j*=2){
		if(j<m && L->r[j]<L->r[j+1])  //左孩子r[j]与右孩子r[j+1]比较
			++j;	//取较大的孩子的下标
		if(temp>=L->r[j])	//较大孩子r[j]与双亲temp比较
			break;
		L->r[s]=L->r[j];	//将较大孩子放置到双亲位置
		s=j;	//记录较大孩子位置
	}
	L->r[s]=temp;	//将双亲插入较大孩子位置
}

小例子：


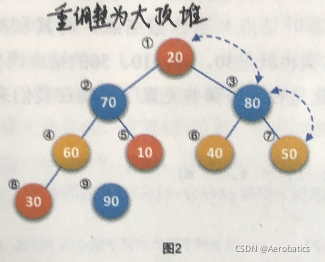
调整为大顶堆后，进行下一次序列调整

具体过程：
一、构建大顶堆（从下往上、从右到左）将每个非叶子结点当作根结点，将其和其子树调整成大顶堆

变量$i$的变化：4 $\to$ 3 $\to$ 2 $\to$ 1，也就是结点30,90,10,50的调整过程

待排序序列{50,10,90,30,70,40,80,60,20}

for(i=9/2=4;i>0;i--)
HeadAdjust(L,4,9)
//void HeapAdjust(SqList *L, int s, int m)
temp=r[4]=30	//r[s]
for(j=2*4=8; j<=9; j*=2) //j=2*s; j<=m
	if(j=8<9 && r[8]=60 < r[9]=20)	//j<m; r[j] < r[j+1]
		++j; //j=9
	//if(r[4]=30 >= r[8]=60) //temp >= r[j]
	r[4]=r[8]=60 //r[s]=r[j]
	s=j=8
r[8]=30 //r[s]=temp

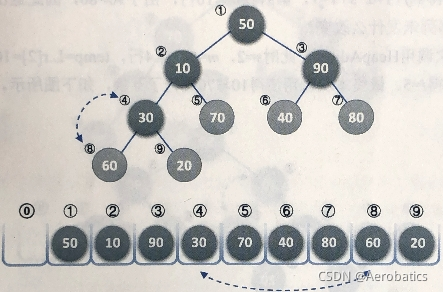
for(i=3;i>0;i--)
HeadAdjust(L,3,9)
//void HeapAdjust(SqList *L, int s, int m)
temp=r[3]=90	//r[s]
for(j=2*3=6; j<=9; j*=2) //j=2*s; j<=m
	//if(j=6<9 && r[6]=40 < r[7]=80)	//j<m; r[j] < r[j+1]
	if(90 >= r[6]=40) //temp >= r[j]
		break;	//退出for循环
r[3]=90; //r[s]=temp

for(i=2;i>;i--)
HeadAdjust(L,2,9)
//void HeapAdjust(SqList *L, int s, int m)
temp=r[2]=10	//r[s]
for(j=2*2=4; j<=9; j*=2) //j=2*s; j<=m
	if(j=4<9 && r[4]=60 < r[5]=70)	//j<m; r[j] < r[j+1]	//左右孩子比较
		++j; //j=5	//取较大的孩子
	//if(10 >= r[5]=70) //temp >= r[j] //双亲与较大孩子比较
	r[2]=r[5]=70	//r[s]=r[j]
	s=j=5
r[5]=10 //r[s]=temp

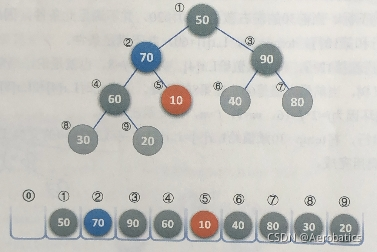
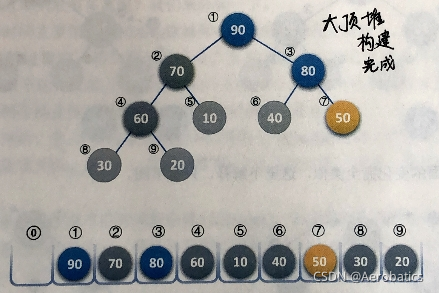
二、排序过程

for(int i=L->length; i>1; i--){   //排序
		swap(L,1,i);	//交换第一个结点(最大值)和第i个结点(当前未排序的子序列的末尾元素交换)
		HeapAdjust(L,1,i-1);	//将r[1]..r[i-1]重新调整为大顶堆
	}

实现步骤

for(i=9; i>1; i--){
 swap(L,1,9);	//swap(L,1,i); 交换90和20
 HeapAdjust(L,1,8);	//HeapAdjust(L,1,i-1);
}
//void HeapAdjust(SqList *L, int s, int m)
temp=r[1];
for(j=2*1=2; j<=8; j*=2) //j=2*s;j<m
	if(j=2 < m=8 && r[2]=70 < r[3]=80)
		++j; //j=3
	//if(r[1]=20 >= r[3]=80) //temp >= r[j]
	r[1]=r[3]=80  //r[s]=r[j]
	s=j=3
//下一轮for
for(j=6; j<=8; j*=2) //j=2*s;j<m
	if(j=6 < m=8 && r[6]=40 < r[7]=50)
		++j //j=7
	//if(r[1]=20 >=  r[7]=50)
	r[3]=r[7]=50	//r[s]=r[j]
	s=j=7
j=2*6=12	//退出for
r[7]=temp=20	//r[s]=temp