哈希表的定义

哈希表增删查效率非常高,趋近于O(1)
没有办法达到绝对的O(1)
哈希表什么时候用到?在进行大量的查询时会用到,只要是有速度快的查询的需求,都会想到哈希表
我们想让这一组数据的查询的时间复杂度是O(1)

不管是存到链表还是数组里面,都是线性的查找,从第一个元素开始查,查一个比较一个,时间复杂度都是O(n)
最快的方法是提供一张表,还是数组, 我们在存的时候,并不是挨个存储,而是元素值的本身作为下标存到数组相应的位置
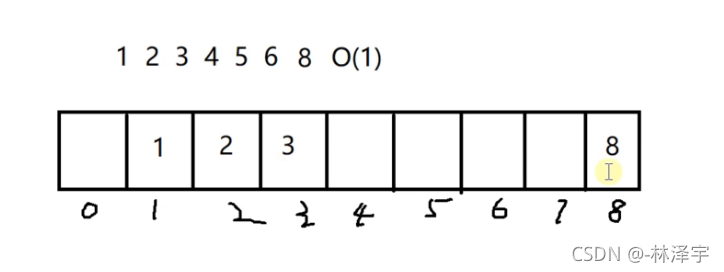
我们把数组的每个位置初始化为-1的值。然后把1,2,3,4,5,6,7,8分别存储在数组下标1,2,3,4,5,6,7,8的地方。
如果是这样存储的话,可能会浪费一些空间。比如说0号位置和7号位置的空间浪费了。这没有关系,关键是它可以提供一个时间复杂度是O(1)的查找的算法。
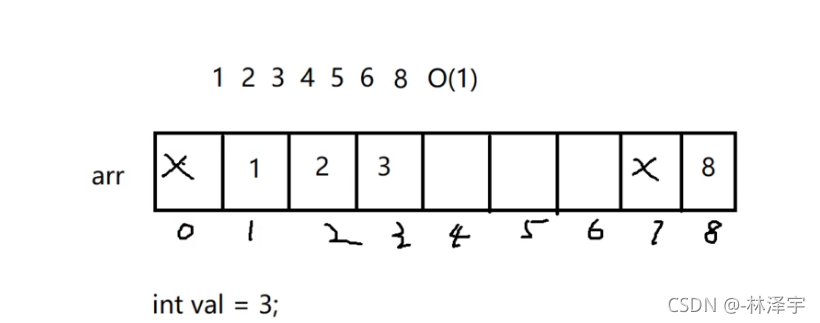
比如说,我现在要查找一个值为3的元素。我直接拿val这个值作为数组的下标去访问 ,如果值是-1,则这个元素3在数组中不存在,如果值不为-1,则3找到了。
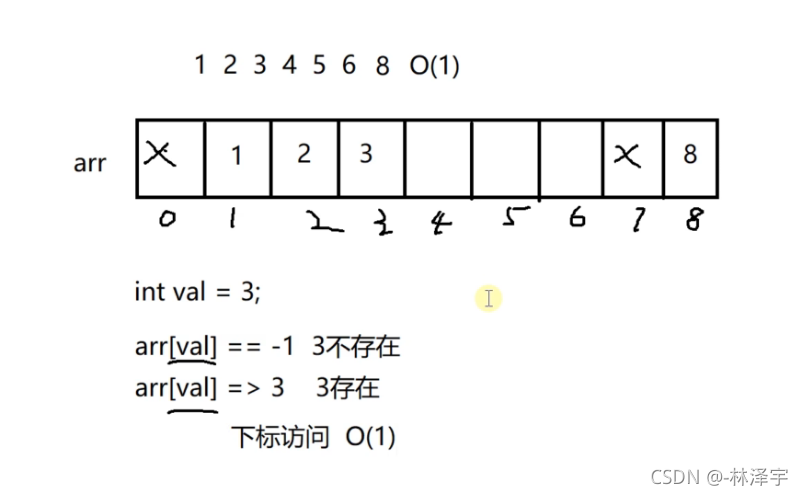
元素的值通过一个映射关系(映射函数)找到元素在表中的存储位置
这张表就称为散列表(哈希表)

但是,上面的方式存储,空间会浪费,比如说是下面这些数字:

如果还是用刚才的映射关系,岂不是要开辟1000003个位置的内存空间?
只有4个位置存储有效元素,其他的那么多的空间位置都浪费了!
在实际的过程中,我们应该为了节省内存空间,找一个合适的映射关系!
常见的映射方法

常见的是除留余数法
假设我们有这么一组数据:

我们定义7个位置大小的数组空间。
元素的值作为输入参数,通过哈希函数处理之后,得到一个输出的值,就是在表中的存储位置,这个表就叫做哈希表或者散列表。
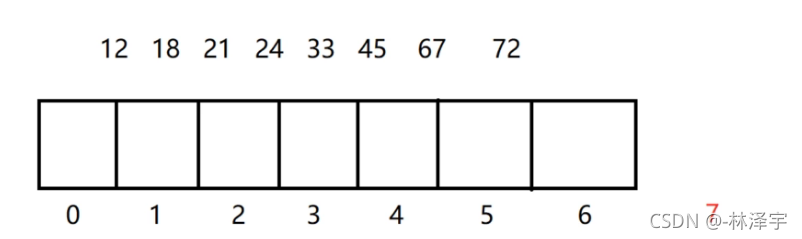
数组的每个位置都初始化为空
我们存储12的话怎么存?除留余数法,余上一个哈希表的长度
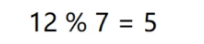
12就存在下标为5的位置。下标为5的位置是空的,所以把12存进去。
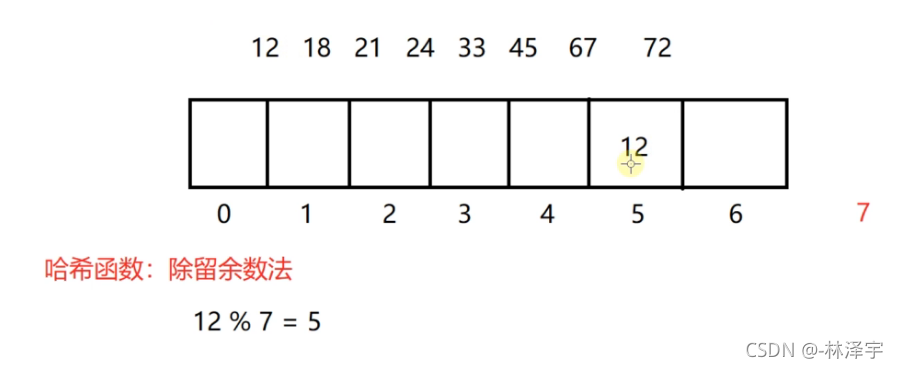
我们接下来要存储18
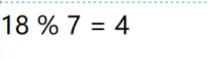
把18这个元素存储在哈希表下标为4的位置
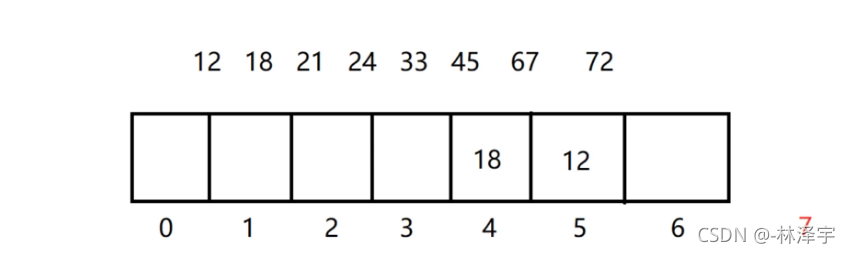
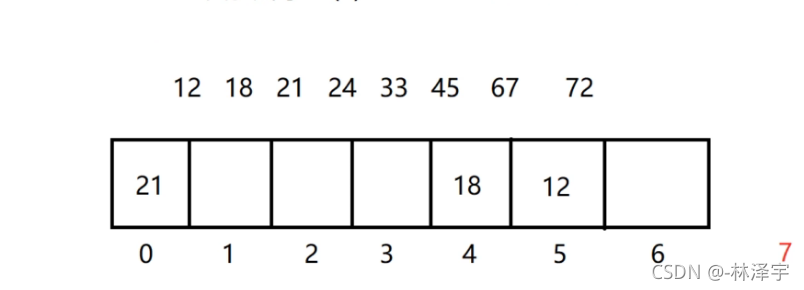
我们接下来存储27
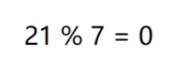
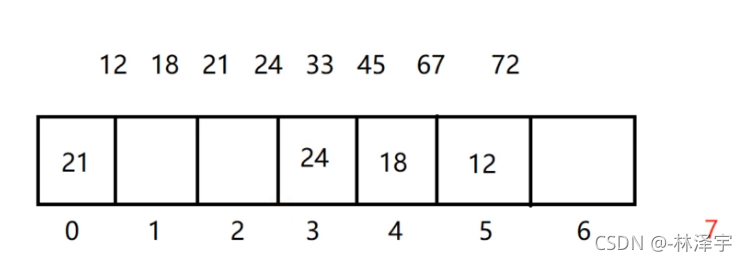
我们接下来存储24
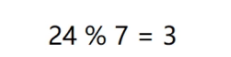
我们接下来存储33
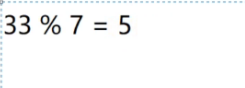
33存储的位置是哈希表下标为5的位置。但是现在哈希表下标为5的位置存储的是12,已经被占用了,而且数组下标这里就这一个位置,这种现象是产生哈希冲突(哈希碰撞)了,怎么办?
不管选择什么样的哈希函数,都会产生哈希冲突,是无法避免的,只能尽量减小哈希冲突产生的概率。
不同元素模上一个7很有可能得到的结果是相同的
解决哈希冲突的方案是什么?

unordered_set和unordered_map底层是用链式哈希表实现的,用链地址法解决哈希冲突
线性探测法:
就是往后继续探测,有空闲的位置就存放。
33经过除留余数法被分到哈希表的5号位置,但是5号位置已经有元素占着了,就把33往后走,找一个空闲的位置存放33
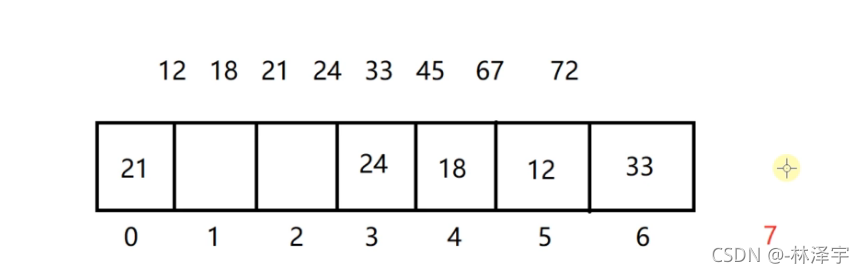
假如我们现在要存储45,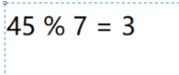
但是3号位置也有元素占用了,往后走,后面的位置都有元素占着了,然后转回首地址往后走,发现1号位置空闲,就把45放到1号位置。(几乎是把数组遍历了一遍了----哈希冲突导致哈希表在存储元素的时候变慢了)
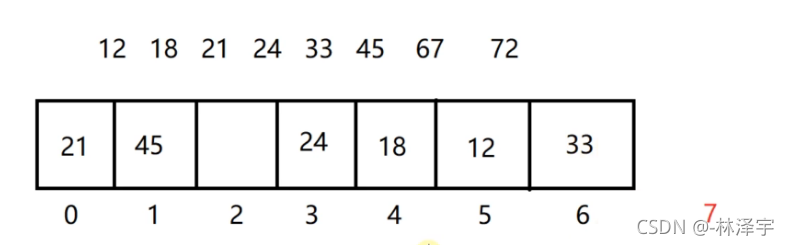
变得有多慢呢???
我们把一个元素按照哈希函数处理之后,放在某一个位置,这个处理是个常量的时间,哈希表在增加元素,时间复杂度是O(1)的,但是由于产生了哈希冲突,如果是用线性探测法,往后找空闲的位置,基本上是把整个哈希表数组遍历了,所以,哈希冲突越多,增加的元素的时间复杂度就从O(1)慢慢的变到了O(n)
现在我们要查询了
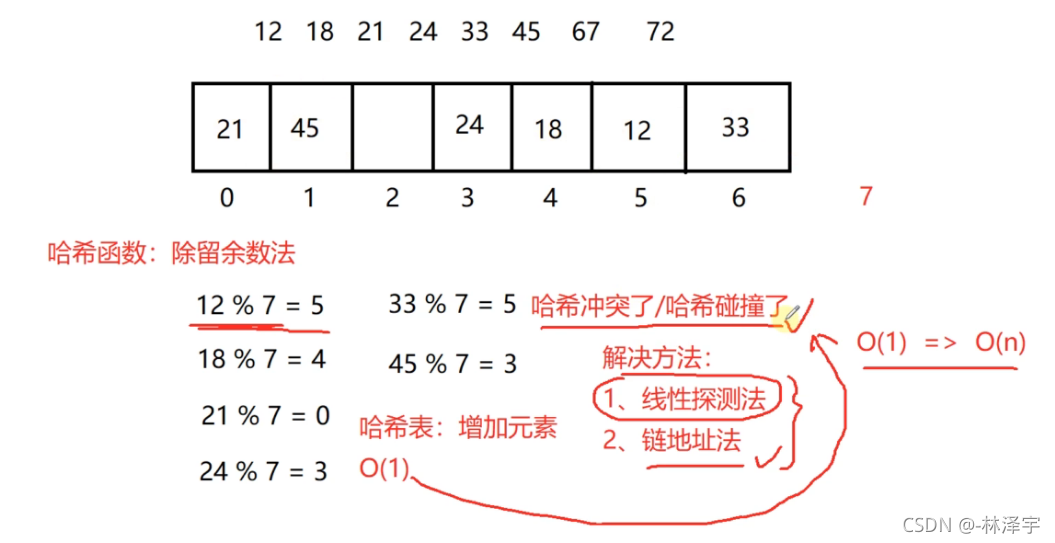
比如说,我们查询18,
18进行哈希函数(除留余数法)得出是4,然后访问4号位置,是18,就查到了
为了在哈希表找18,先执行了一次哈希函数采用的除留余数法,是常量时间,然后进行哈希表数组的下标访问,也是一个常量时间 
但是同样的,因为哈希冲突的存在,比如我要查45,先进行哈希函数的除留余数法,得出3,访问3号位置,发现3号位置上的元素是24而不是45,肯定当时往哈希表放45的时候已经产生哈希冲突了,所以45并没有在3号位置上放,我们还得知道这个哈希表解决哈希冲突的方案是什么:是线性探测法
就和环形队列一样,往后遍历,然后走环,最终在1号位置上找到了45,因为哈希冲突及线性探测法的存在,导致搜索的时间复杂度从O(1)–>O(n)
哈希表的删除元素的时间复杂度也是O(1),我们删除18,通过哈希表的除留余数法,得到4,4号位置就是18,所以就直接把18干掉了O(1)的操作
但是,如果我们要删除45,通过哈希表的除留余数法,得到3,发现3号位置不是45, 得知原来在插入45的时候产生了哈希冲突了,因为是线性探测法解决哈希冲突,又是环形的遍历,然后查到1号位置的元素是45,然后把45删掉。 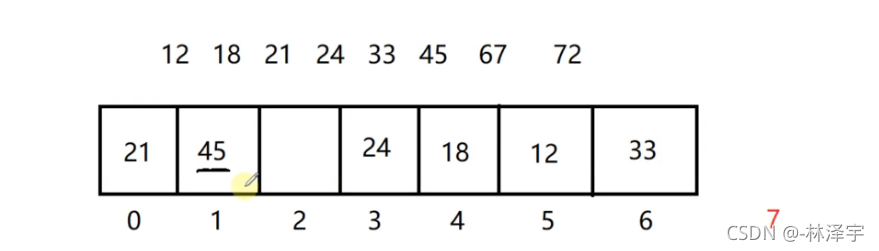
在寻找45的时候发生了哈希冲突,导致删除的时间复杂度从O(1)–>O(n)
当我们在哈希表存放的元素越来越多,哈希冲突的发生概率也就越来越大
在增删查的时间复杂度从O(1)—>O(n)
实际上,我们会在多种情况下去优化,去降低哈希冲突的概率,但是是不能杜绝的。
降低哈希冲突的概率
方法1:我们在哈希函数上去想办法:
对于除留余数法来说,我们希望通过模上一个哈希表的长度后, 尽量产生的结果是离散的,而不是经常产生相同值导致哈希冲突 我们尽量让哈希表的长度(哈希桶的长度):取素数,只有1和自己能被整除,这样通除留余数产生的结果相同的概率就很低了
在C++的容器里,有专门定义一张素数表,在进行扩容的时候,采用的哈希函数是除留余数法的话,会采用素数 ,把所有的素数都枚举了一下
哈希表在扩容的时候,取的下一个长度就是在素数表里面的下一个素数
方法2:哈希表的装载因子 loadfactor
装载因子:以占用位置(桶)的个数除以桶的总个数。
Java中或者C++链式哈希表实现的容器或者集合,装载因子值取的默认值是0.75或者四分之三

如果已占用桶的个数占到总的桶个数的四分之三的话,我们就说,此时这个哈希表放的元素已经比较多了,再继续放元素,产生的哈希冲突的概率就大 ,进而导致哈希表的增删查的时间复杂度变大,效率越来越低了。
此时如果是下面这个情况,哈希表就需要扩容了:

哈希表扩容以后,相当于数组的扩容,造价还是很大的,需要开辟更大长度的空间,采用素数的长度开辟更长的哈希表。
这时候,原来的元素就要放在新的哈希表里面了。
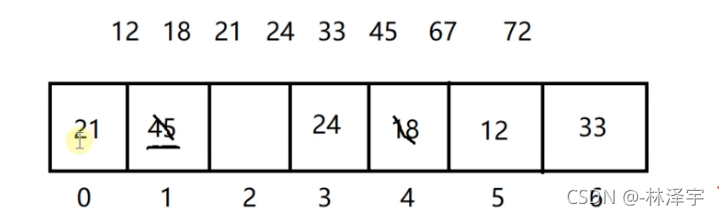
如果这个21原来放在旧的哈希表是0号位置,那么它在新的哈希表存放的也是一定在0号位置吗?
这个当然是不能确定的。
比如说当时哈希表的桶的个数是7,扩容之后,新的哈希表的桶的个数是23,那么除留余数法的模的数就不一样了,得到的值就不一定和原来一样了。
所以,对于哈希表的扩容来说,造价还是挺大的

扩容的时间复杂度是O(n)
哈希表的增删查时间复杂度:

因为并不是每次增加哈希表的元素都会触发哈希表的扩容,可能在第n次才触发到。

包括之间的vector的扩容,末尾元素增加,本身是O(1),但是如果末尾元素增加没有空间了, 导致数组需要先扩容了,扩容的话就是O(n),但是并不是每次末尾元素增加都会导致扩容啊,所以vector的末尾元素的增加的均摊时间复杂度是O(1)