开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 向量旋转和坐标系旋转问题 -> 正文阅读

[数据结构与算法]向量旋转和坐标系旋转问题

参考资料

博客——旋转矩阵

MathWorks中国官网rotx说明]

向量旋转问题

空间中存在一个向量，在坐标系C中的表示为v，则v绕坐标系C的某个坐标轴旋转一定角度后，求该向量在坐标C中的表示v1。

MathWorks中国官网rotx说明中给出了这个问题的答案

$R_{x}(\alpha)=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right]$

$R_{y}(\beta)=\left[\begin{array}{ccc} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{array}\right]$

$R_{z}(\gamma)=\left[\begin{array}{ccc} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{array}\right]$

根据欧拉旋转定理和MathWorks中国官网rotx说明可得:

$\mathbf{v}^{\prime}=R \mathbf{v}=R_{z}(\gamma) R_{y}(\beta) R_{x}(\alpha) \mathbf{v}$

总体向量旋转矩阵R的展开表达式为：

$R =\left[\begin{array}{ccc} \cos(\beta)\cos(\gamma) & \cos(\gamma)\sin(\alpha)\sin(\beta) - \cos(\alpha)\sin(\gamma) & \sin(\alpha)\sin(\gamma) + \cos(\alpha)\cos(\gamma)\sin(\beta) \\ \cos(\beta)\sin(\gamma) & \cos(\alpha)\cos(\gamma) + \sin(\alpha)\sin(\beta)\sin(\gamma) & \cos(\alpha)\sin(\beta)\sin(\gamma) - \cos(\gamma)\sin(\alpha) \\ -\sin(\beta) & \cos(\beta)\sin(\alpha) & \cos(\alpha)\cos(\beta) \end{array}\right]$

?向量旋转问题

坐标系旋转问题

空间中存在一个向量，在坐标系C中的表示为v，则坐标系C绕自己的某个坐标轴旋转一定角度后变为坐标系C1，求该向量在坐标系C1中的表示v1。

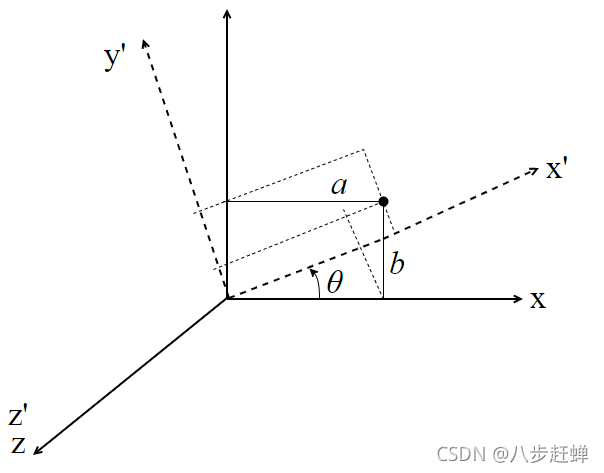
?新坐标系沿原始坐标系z轴旋转角度θ，则在原始
坐标系下坐标为(a, b, 0)的点在新坐标系下坐标为
(a*cos(θ)+b*sin(θ), b*cos(θ)-a*sin(θ), 0)

博客——旋转矩阵中给出了旋转矩阵的推导结果

$R_{x}(\alpha)=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha \\ 0 & -\sin \alpha & \cos \alpha \end{array}\right]$

$R_{y}(\beta)=\left[\begin{array}{ccc} \cos \beta & 0 & -\sin \beta \\ 0 & 1 & 0 \\ \sin \beta & 0 & \cos \beta \end{array}\right]$

$R_{z}(\gamma)=\left[\begin{array}{ccc} \cos \gamma & \sin \gamma & 0 \\ -\sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{array}\right]$

如果新坐标系是原始坐标系沿着原始坐标系的x轴旋转\alpha角度后形成的，则在原始坐标系下表示为v的向量在新坐标系下的表示v'为：

$\mathbf{v}^{\prime}=R_{x}(\alpha) \mathbf{v}$

如果新坐标系是原始坐标系沿着原始坐标系的y轴旋转\beta角度后形成的，则在原始坐标系下表示为v的向量在新坐标系下的表示v'为：

$\mathbf{v}^{\prime}=R_{y}(\beta) \mathbf{v}$

如果新坐标系是原始坐标系沿着原始坐标系的z轴旋转\gamma角度后形成的，则在原始坐标系下表示为v的向量在新坐标系下的表示v'为：

$\mathbf{v}^{\prime}=R_{z}(\gamma) \mathbf{v}$

?坐标系旋转问题

更复杂的问题

空间中存在一个向量，在坐标系C中的表示为v，在坐标系C1中的表示为v1，则坐标系C1绕坐标系C的某个坐标轴旋转一定角度后变为坐标系C2，求该向量在坐标系C2中的表示v2。

该问题，本质上还是坐标系旋转问题，如果能将“坐标系C1绕坐标系C的某个坐标轴旋转一定角度”这个过程转换为“坐标系C1绕坐标系C1自己的坐标轴旋转一定角度”，则该问题就转换成了上文中的问题2——坐标系旋转问题，具体转换方法应该是需要借助v于v1的关系。

Matlab代码

%% ***************************** 坐标系旋转问题和向量旋转问题 ****************************%
% 参考资料：
% 博客——旋转矩阵：https://www.pianshen.com/article/20691116374/
% MathWorks中国官网：https://ww2.mathworks.cn/help/phased/ref/rotx.html?searchHighlight=rotx&s_tid=srchtitle

% 1.坐标系旋转问题
%  空间中存在一个向量v，在三维笛卡尔坐标系C中的坐标表示为v，如果另一个三维笛卡尔坐标系C'是
%  沿着坐标系C的x（或y或z）轴旋转一定角度后形成的，求原向量v在新坐标系C'下的表示v'。
% 2.向量旋转问题
%  空间中存在一个向量v，在三维笛卡尔坐标系C中的坐标表示为v，如果该向量沿着坐标轴旋转一定角
%  度，求旋转后的原向量的表示v'。

%**************************************************************************************************%
%                                            坐标系旋转问题                                         %
%**************************************************************************************************%
clc;close all;clear all;fclose('all');
%------------------------------------------------ 输入 --------------------------------------------%
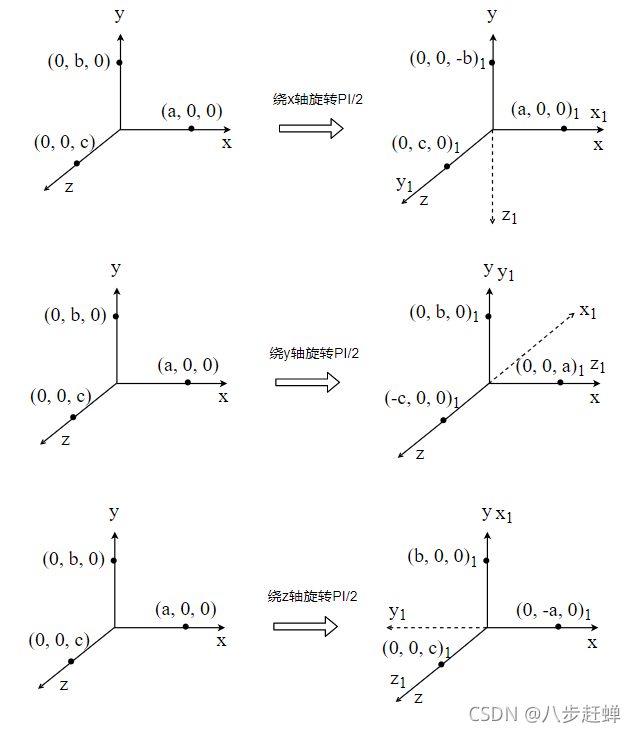
a = 2;
b = 3;
c = 4;
% 三个列向量在原始坐标系内的表示
v = [a, 0, 0;
     0, b, 0;
     0, 0, c]; 
% 新坐标系绕原始坐标系x/y/z轴旋转的弧度
RxRad = pi / 2;  % 绕X轴旋转的弧度
RyRad = pi / 2;  % 绕Y轴旋转的弧度
RzRad = pi / 2;  % 绕Z轴旋转的弧度
% 平移向量
Move = [0, 0, 0].';

%---------------------------------------------- 目标输出 -------------------------------------------%
vx1aim = [a, 0, 0;
         0, 0,  c;
         0, -b, 0];
vy1aim = [0, 0, -c;
         0, b, 0;
         a, 0, 0];
vz1aim = [0,  b,  0;
         -a, 0,  0;
         0,  0,  c];
%-------------------------------------------- 计算旋转矩阵 -----------------------------------------%    
% 绕X轴旋转的旋转矩阵
Rx = [1,           0,          0;
      0,           cos(RxRad), sin(RxRad);
      0,           -sin(RxRad), cos(RxRad)];

% 绕Y轴旋转的旋转矩阵               
Ry = [cos(RyRad),  0,          -sin(RyRad);
      0,           1,          0;
      sin(RyRad),  0,          cos(RyRad)];

% 绕Z轴旋转的旋转矩阵
Rz = [cos(RzRad),  sin(RzRad),  0;
      -sin(RzRad), cos(RzRad),  0;
      0,           0,           1];
     
%---------------------------------------------- 实际输出 -------------------------------------------%
vx1result = Rx * v;
vy1result = Ry * v;
vz1result = Rz * v;

%---------------------------------------------- 结果验证 -------------------------------------------%
vx1aim - vx1result
vy1aim - vy1result
vz1aim - vz1result

%**************************************************************************************************%
%                                             向量旋转问题                                          %
%**************************************************************************************************%
clc;close all;clear all;fclose('all');
%------------------------------------------------ 输入 ---------------------------------------------%
a = 2;
b = 3;
c = 4;
% 三个列向量在原始坐标系内的表示
v = [a, 0, 0;
     0, b, 0;
     0, 0, c]; 
% 新坐标系绕原始坐标系x/y/z轴旋转的弧度
RxRad = pi / 2;  % 绕X轴旋转的弧度
RyRad = pi / 2;  % 绕Y轴旋转的弧度
RzRad = pi / 2;  % 绕Z轴旋转的弧度
% 平移向量
Move = [0, 0, 0].';

%---------------------------------------------- 目标输出 -------------------------------------------%
vx1aim = [a, 0, 0;
         0, 0,  -c;
         0, b, 0];
vy1aim = [0, 0, c;
         0, b, 0;
         -a, 0, 0];
vz1aim = [0,  -b,  0;
         a, 0,  0;
         0,  0,  c];
%-------------------------------------------- 计算旋转矩阵 -----------------------------------------%    
% 绕X轴旋转的旋转矩阵
% 对应Matlab内置函数rotx
Rx = [1,           0,          0;
      0,           cos(RxRad), -sin(RxRad);
      0,           sin(RxRad), cos(RxRad)];

% 绕Y轴旋转的旋转矩阵
% 对应Matlab内置函数roty
Ry = [cos(RyRad),  0,          sin(RyRad);
      0,           1,          0;
      -sin(RyRad),  0,         cos(RyRad)];

% 绕Z轴旋转的旋转矩阵
% 对应Matlab内置函数rotz
Rz = [cos(RzRad),  -sin(RzRad),  0;
      sin(RzRad), cos(RzRad),    0;
      0,           0,           1];
     
%---------------------------------------------- 实际输出 -------------------------------------------%
vx1result = Rx * v;
vy1result = Ry * v;
vz1result = Rz * v;

%---------------------------------------------- 结果验证 -------------------------------------------%
vx1aim - vx1result
vy1aim - vy1result
vz1aim - vz1result


%**************************************************************************************************%
%                                     总体向量旋转矩阵R的表达式推导                                  %
%**************************************************************************************************%
% 如果一个向量v先后绕x、y、z轴旋转。求旋转后的向量v1的表达式。根据上文介绍的向量旋转问题，可知旋转后的向量
% 表达式应为v1 = Rz * Ry * Rx * v = R * v
clc;close all;clear all;fclose('all');

syms RxRad RyRad RzRad Rx Ry Rz R tmp
% 绕X轴旋转的旋转矩阵
% 对应Matlab内置函数rotx
Rx = [1,           0,          0;
      0,           cos(RxRad), -sin(RxRad);
      0,           sin(RxRad), cos(RxRad)];

% 绕Y轴旋转的旋转矩阵
% 对应Matlab内置函数roty
Ry = [cos(RyRad),  0,          sin(RyRad);
      0,           1,          0;
      -sin(RyRad),  0,          cos(RyRad)];

% 绕Z轴旋转的旋转矩阵
% 对应Matlab内置函数rotz
Rz = [cos(RzRad),  -sin(RzRad),  0;
      sin(RzRad), cos(RzRad),  0;
      0,           0,           1];
% 总体转换矩阵
R = Rz * Ry * Rx;

% 推导结果为
R = [cos(RyRad)*cos(RzRad), cos(RzRad)*sin(RxRad)*sin(RyRad) - cos(RxRad)*sin(RzRad), sin(RxRad)*sin(RzRad) + cos(RxRad)*cos(RzRad)*sin(RyRad);
     cos(RyRad)*sin(RzRad), cos(RxRad)*cos(RzRad) + sin(RxRad)*sin(RyRad)*sin(RzRad), cos(RxRad)*sin(RyRad)*sin(RzRad) - cos(RzRad)*sin(RxRad);
     -sin(RyRad),           cos(RyRad)*sin(RxRad),                                    cos(RxRad)*cos(RyRad)];

% 封装为函数
function R = computeR(rot)
%计算总体向量旋转矩阵R = Rz * Ry * Rx
% 输入：
% rot(1)：绕X轴旋转的弧度
% rot(2)：绕Y轴旋转的弧度
% rot(3)：绕Z轴旋转的弧度

% 输出
% R：总体向量旋转矩阵R

% 坐标系旋转角度
RxRad = rot(1);  % 绕X轴旋转的弧度
RyRad = rot(2);  % 绕Y轴旋转的弧度
RzRad = rot(3);  % 绕Z轴旋转的弧度

R = [cos(RyRad)*cos(RzRad), cos(RzRad)*sin(RxRad)*sin(RyRad) - cos(RxRad)*sin(RzRad), sin(RxRad)*sin(RzRad) + cos(RxRad)*cos(RzRad)*sin(RyRad);
     cos(RyRad)*sin(RzRad), cos(RxRad)*cos(RzRad) + sin(RxRad)*sin(RyRad)*sin(RzRad), cos(RxRad)*sin(RyRad)*sin(RzRad) - cos(RzRad)*sin(RxRad);
     -sin(RyRad),           cos(RyRad)*sin(RxRad),                                    cos(RxRad)*cos(RyRad)];

end

%**************************************************************************************************%
%                                        总体向量旋转矩阵R的验证                                     %
%**************************************************************************************************%
clc;close all;clear all;fclose('all');
%------------------------------------------------ 输入 ---------------------------------------------%
a = 2;
b = 3;
c = 4;
% 三个列向量在原始坐标系内的表示
v = [a, 0, 0;
     0, b, 0;
     0, 0, c]; 
% 新坐标系绕原始坐标系x/y/z轴旋转的弧度
rot1 = [pi / 2, 0, 0];  % 绕x、y、z轴旋转的弧度
rot2 = [pi / 2, pi / 2, 0];  % 绕x、y、z轴旋转的弧度
rot3 = [pi / 2, pi / 2, pi / 2];  % 绕x、y、z轴旋转的弧度

%---------------------------------------------- 目标输出 -------------------------------------------%
v1aim = [a, 0, 0;
         0, 0, -c;
         0, b, 0];
v2aim = [0, b, 0;
         0, 0, -c;
         -a,0, 0];
v3aim = [0, 0, c;
         0, b, 0;
         -a,0, 0];
%-------------------------------------------- 计算旋转矩阵 -----------------------------------------%    
R1 = computeR(rot1);
R2 = computeR(rot2);
R3 = computeR(rot3);
     
%---------------------------------------------- 实际输出 -------------------------------------------%
v1result = R1 * v;
v2result = R2 * v;
v3result = R3 * v;

%---------------------------------------------- 结果验证 -------------------------------------------%
v1aim - v1result
v2aim - v2result
v3aim - v3result

%**************************************************************************************************%
%                                     总体坐标系旋转矩阵R的表达式推导                                %
%**************************************************************************************************%
% 坐标系C1与原始坐标系C重合，如果坐标系C1先后绕原始坐标系C的x、y、z轴旋转成为坐标系C2。求旋转前在原始坐标系C中表示为v的
% 向量，在坐标系C2的表达式v2。
clc;close all;clear all;fclose('all');

syms RxRad RyRad RzRad Rx Ry Rz R tmp
% 绕X轴旋转的旋转矩阵
% 对应Matlab内置函数rotx(-RxRad*180/pi)
Rx = [1,           0,          0;
      0,           cos(RxRad), sin(RxRad);
      0,           -sin(RxRad), cos(RxRad)];

% 绕Y轴旋转的旋转矩阵
% 对应Matlab内置函数roty(-RyRad*180/pi)
Ry = [cos(RyRad),  0,          -sin(RyRad);
      0,           1,          0;
      sin(RyRad),  0,          cos(RyRad)];

% 绕Z轴旋转的旋转矩阵
% 对应Matlab内置函数rotz(-RzRad*180/pi)
Rz = [cos(RzRad),  sin(RzRad),  0;
      -sin(RzRad), cos(RzRad),  0;
      0,           0,           1];
% 总体转换矩阵
R = Rx * Ry * Rz;

% 推导结果为
R = [cos(RyRad)*cos(RzRad),                                    cos(RyRad)*sin(RzRad),                                    -sin(RyRad);
     cos(RzRad)*sin(RxRad)*sin(RyRad) - cos(RxRad)*sin(RzRad), cos(RxRad)*cos(RzRad) + sin(RxRad)*sin(RyRad)*sin(RzRad), cos(RyRad)*sin(RxRad);
     sin(RxRad)*sin(RzRad) + cos(RxRad)*cos(RzRad)*sin(RyRad), cos(RxRad)*sin(RyRad)*sin(RzRad) - cos(RzRad)*sin(RxRad), cos(RxRad)*cos(RyRad)];
% 可以看到，本节推导出的总体坐标系旋转矩阵与前面推导出来的总体向量旋转矩阵是互为转置的关系

%**************************************************************************************************%
%                                        总体坐标系旋转矩阵R的验证                                   %
%**************************************************************************************************%
clc;close all;clear all;fclose('all');
%------------------------------------------------ 输入 ---------------------------------------------%
a = 2;
b = 3;
c = 4;
% 三个列向量在原始坐标系内的表示
v = [a, 0, 0;
     0, b, 0;
     0, 0, c]; 
% 新坐标系绕原始坐标系x/y/z轴旋转的弧度
rot1 = [pi / 2, 0, 0];  % 绕x、y、z轴旋转的弧度
rot2 = [pi / 2, pi / 2, 0];  % 绕x、y、z轴旋转的弧度
rot3 = [pi / 2, pi / 2, pi / 2];  % 绕x、y、z轴旋转的弧度

%---------------------------------------------- 目标输出 -------------------------------------------%
v1aim = [a, 0, 0;
         0, 0, c;
         0, -b, 0];
v2aim = [0, 0, -c;
         a, 0, 0;
         0,-b, 0];
v3aim = [0, 0, -c;
         0, b, 0;
         a,0, 0];
%-------------------------------------------- 计算旋转矩阵 -----------------------------------------%
R1 = computeR(rot1).';
R2 = computeR(rot2).';
R3 = computeR(rot3).';
     
%---------------------------------------------- 实际输出 -------------------------------------------%
v1result = R1 * v;
v2result = R2 * v;
v3result = R3 * v;

%---------------------------------------------- 结果验证 -------------------------------------------%
v1aim - v1result
v2aim - v2result
v3aim - v3result

说明：

旋转矩阵表达式的推导没有限定坐标系是左手坐标系还是右手坐标系，所以旋转矩阵表达式同时适用于左手和右手表达式。

数据结构与算法最新文章

【力扣106】从中序与后续遍历序列构造二叉

leetcode 322 零钱兑换

哈希的应用：海量数据处理

动态规划|最短Hamilton路径

华为机试_HJ41 称砝码【中等】【menset】【

【C与数据结构】——寒假提高每日练习Day1

基础算法——堆排序

2023王道数据结构线性表--单链表课后习题部

LeetCode 之反转链表的一部分