题目描述
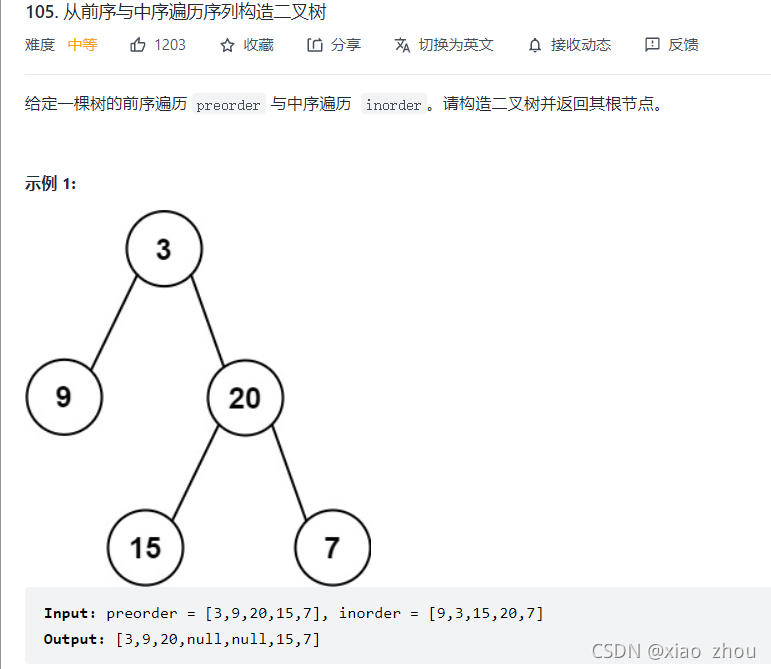
原理分析
(1)大致思路
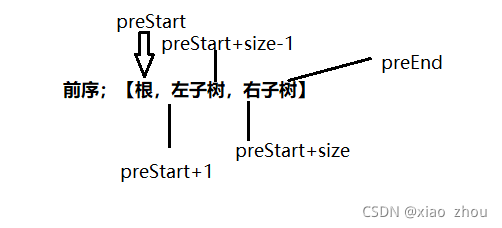
下面讲解一下,前序遍历+中序遍历如何确定一个唯一的二叉树。关于二叉树的基本知识,请看二叉树的基本操作及联系。对此就不再过多重复。对于前序遍历顺序:根、左子树、右子树;对于中序的遍历顺序:左子树、根、右子树。所以通过前序遍历,我们获取前序第一个结点就是这个树的根,再在中序遍历中找到该结点的位置。在中序中,根的左边全部的是属于根左子树的结点,根的右边全是属于根的右子树的结点。
详细如图:
做完第一步之后,我们会发现,我们目前只具体确定了哪一个是根节点,哪些结点分别属于左右子树。但是由于树的递归特性。属于左子树的结点仍然符合前序遍历,中序遍历特点的。所以我们就是需要对刚刚分离出来的两部分分别再次用上述的方法,确定根节点,确定哪些结点属于左子树,哪些结点属于右子树。一次类推,直到结束。这就是这道题的大致思路。
(2)细节阐述
这道题还是有不少值得思考的地方。
1、我们如何表示哪些结点是属于左子树,右子树?
答:前序、中序的给出都vector,所以我们可以通过下标确定范围来做到。前序:【根,左子树,右子树】。中序:【左子树,根,右子树】。他们都是三种类别结点都是集中在一起,很好区分。
2、递归的结束条件是什么?
答:这个还是要结合具体代码分析,目前可以确定的是,当我们控制范围时,如果出现范围不合法(不存在)的情况就说明已经没有左子树或者右子树了,就要返回。
代码实现
注:一般在我的题解中,范围控制,代码这样书写的原因都会通过注释的方式写在对应代码旁边,帮助读者理解分析代码,这样更有针对性。因此,如果读者对于前面的题目分析有疑惑或者不理解的地方,请仔细阅读代码及旁边注释,一定会对你有所启发,帮助你的理解!!
(1)主函数
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
//_buildTree本题因为需要递归实现,因此需要借助一个递归函数。
return _buildTree(preorder,0,preorder.size()-1,inorder,0,inorder.size()-1);
}
我在这里要详细说明一下这个递归函数的各个参数及作用
第一个参数:就是前序遍历的vector,没有太多需要解释的
第二个参数:preStart,就是在子问题种前序的起始位置。详细的说,就是我们在确定根以后,我们就要递归左右子树,左右子树的起始位置是哪里就要确定。
第三个参数:preEnd:就是在子问题种前序的终止位置,这样就保证preStart与preEnd之间是子问题的结点序列。
第四个参数就是中序遍历的vector
第五个参数:inStart,就是在子问题中中序遍历的起始位置
第六个参数:inEnd,就是在子问题种中序遍历的结束位置
(2)递归函数
TreeNode* _buildTree(vector<int>& preorder,int preStart,int preEnd,vector<int>&inorder,int inStart,int inEnd)
{
if(preStart>preEnd)
{
return nullptr;
}
//我们可以直接确定根节点,所以我们首先创建出根节点
TreeNode* root = new TreeNode(preorder[preStart]);
//找到根节点后,我们拿着根节点的值在中序遍历中找到对应位置,区分左右子树
for(int i=inStart;i<=inEnd;i++)
{
//找到根节点所在的中序遍历的位置
if(inorder[i] == preorder[preStart])
{
//由于递归函数完成子问题树的构建,所有让大问题的root左右子树分别链接即可
root->left = _buildTree(preorder,preStart+1,preStart+i-inStart,inorder,inStart,i-1);
root->right = _buildTree(preorder,preStart+i-inStart+1,preEnd,inorder,i+1,inEnd);
}
}
return root;
}
参数区间的决定
关键就是在递归子问题的时候传参数是多少。
size:size是左子树中的结点个数所以size = i-inStart
所以:root->left = _buildTree(preorder,preStart+1,preStart+i-inStart,inorder,inStart,i-1);
xxxxxxroot->right = _buildTree(preorder,preStart+i-inStart+1,preEnd,inorder,i+1,inEnd);
读者自行比较即可理解
递归结束的条件
接下来就是判断如何结束递归,就是递归函数中的第一个if。之前我们提到过,如果子问题子树的区间不存在就可以结束循环了,那么怎么才叫不存在呢?
我们刚刚获得了每一个子树的前序的范围【preStart,preEnd】,如果preStart==preEnd时候,就说明子树还有一个结点,仍然需要循环,但是有没有可能preStart>preEnd呢?答案是肯定的。我们发现递归子问题的时候preStart = preStart+1,preStart不断增大,而递归子问题时preEnd = preStart+size-1。
分析比较得:当子树只有一个结点(size == 1)是,preStart == preEnd。再递归一次后,size == 0,因此preStart > preEnd。就说明没有子树了,可以返回nullptr了。
所以得到代码:if (preStart>preEnd) return nullptr;
总结
xxxx看到二叉树问题,我们首相应该想到的就是函数递归,因而二叉树具有很好的“递归特性”,每一个子树都是二叉树,都满足树的特性,子问题具有一样的特性就可以使用递归算法。其次我们应该明确知道,二叉树的“前、中、后,层序遍历”,并且知道他们之间的关系联系以及区别。在有以上的思想以及储备知识后,我们就可以写出具有一定思路的代码逻辑。这道题还有一个比较重要的地方就是控制子问题的前序、中序vector的范围界限。真正保证子问题与原问题的统一
xxxx这就是这道题的完整解析,如果大家有更好的思路,或者我代码中可优化的地方,请指出,我一定虚心学习。希望我们一起学习,一起进步!!