开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 数据结构：队列和栈的详解 -> 正文阅读

[数据结构与算法]数据结构：队列和栈的详解

栈

栈的结构和概念

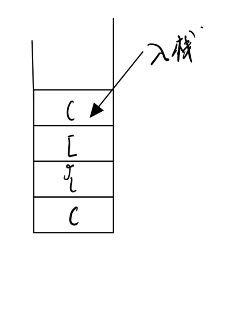
栈：一种特殊的线性表，其中只允许在固定的一端进行插入和删除元素。进行数据插入和删除操作的一段称为栈顶，另一端称为栈底。栈中的元素遵循先进后出的原则。
压栈：栈的插入操作叫做进栈/入栈/压栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈，出数据也在栈顶。

栈的实现

栈的实现一般可以使用数组或者链表，但是数组的结构要更优一点。因为数组在尾上插入数据的代价比较小。

其实两种数据结构都可以实现链表，但是为什么选择数组呢
因为由于栈的特性，使得如果使用链表，那么栈顶也就是出入元素的位置在链表的末尾，每次入栈、出栈都要从头节点遍历整个链表。

栈的实现：

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>


typedef int Datatype;
typedef struct Stack
{
	Datatype* a;
	int top;
	int Capacity;
}Stack;

void StackInit(Stack* p);   //初始化栈
void StackPush(Stack* p, Datatype x);  //入栈操作
void StackPop(Stack* p);    //出栈操作
Datatype StackTop(Stack* p);   //返回栈顶元素的值
int StackEmpty(Stack* p);    //检查栈是否为空
void StackDestroy(Stack* p);   //销毁栈
void StackPrint(Stack* p);     //打印栈的元素

以上时栈的结构和具体的基本操作

下面是这些具体操作的实现

#define _CRT_SECURE_NO_WARNINGS 1
#include"stack.h"
void StackInit(Stack* p)
{
	assert(p);
	p->a = (Datatype *)malloc(4*sizeof(Datatype));
	p->top = 0;
	p->Capacity = 4;
}
void StackPush(Stack* p, Datatype x)
{
	assert(p);
	if (p->top == p->Capacity)  //检查是否要增容
	{
		p->a = (Datatype *)realloc(p->a,2 * p->Capacity*sizeof(Datatype));
		p->Capacity = p->Capacity * 2;
	}
	p->a[p->top] = x;
	p->top++;
}
void StackPop(Stack* p)
{
	assert(p);
	if(p->top)
	p->top = p -> top - 1;
}
void StackPrint(Stack* p)
{
	assert(p);
	for (int i = 0; i < p->top; i++)
	{
		printf(" %d ", p->a[i]);
	}
	printf("\n");
}
Datatype StackTop(Stack* p)
{
	return p->a[p->top - 1];
}
int StackEmpty(Stack* p)
{
	return p->top == 0;
}
void StackDestroy(Stack* p)
{
	free(p->a);
	p->a = NULL;
	p->top = 0;
	p->Capacity = 0;
}

栈的一些应用

括号匹配问题

leetcode——原题

//上面要引用栈的实现和相应实现的函数，为了能更清晰的看判断函数，我就不在前面复制了
bool isValid(char * s){
    Stack ps;
    StackInit(&ps);
    while(*s)
    {
        if(*s=='(' || *s=='{' || *s=='[')
        {
            StackPush(&ps,*s);
            s++;
        }
        else
        {
            if(StackEmpty(&ps))
            return false;
            char top=StackTop(&ps);
            StackPop(&ps);
            if((top=='[' && *s!=']')||(top=='{' && *s!='}')||(top=='(' && *s!=')'))
            return false;
            s++;
        }
    }
    if(StackEmpty(&ps))
    return true;
    return false;
}

这题的思路是：

循环遍历字符串s，如果*s是 ‘(’ 、’{’、 ‘[’ 中的任意一个，就将该字符入栈
如果*s不是以上字符也就是’)’ 、’}’、 ‘]’ ，那就那他和栈顶的元素进行匹配，如果匹配了就将栈顶的元素出栈，不匹配就直接return false结束判断。循环完成返回return true

但是还是要注意一些特殊情况：

当字符串为 “(” 时，这时就要在末尾的return true前面判断栈是否为空，如果栈不为空，说明栈里面还有未匹配的字符，所以要返回false
当字符串为")"时，我们要在第二部也就时取栈顶元素之前判断栈是否为空，如果为空的话，就说明栈里面没有与右括号所匹配的左括号，返回false

用栈实现队列

leetcode-用栈实现队列
用队列实现栈主要的难点是在出栈和返回栈顶元素两个操作上
但是两个函数思路是一摸一样的
以出栈函数 myQueuePop函数为例
在这里插入图片描述
这里为了实现队列，我们要创建两个栈来相互倒来将队首元素拿出，具体操作如下：

首先将s1栈的栈顶元素入到s2栈中，然后将栈顶元素出栈。重复上述操作直到s1栈为空。
这时整个栈的元素相当于逆置了，队首元素现在在栈顶的位置，下面的操作在 myQueuePop和myQueuePeek操作略有不同
```
           -  myQueuePop 要把s2栈顶的值出栈
           - myQueuePeek 不用把s2的栈顶的值
```
最后首先将s2栈的栈顶元素入到s1栈中，然后将栈顶元素出栈。重复上述操作直到s2栈为空

代码：

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>


typedef int Datatype;
typedef struct Stack
{
	Datatype* a;
	int top;
	int Capacity;
}Stack;
void StackInit(Stack* p)
{
	assert(p);
	p->a = (Datatype*)malloc(4 * sizeof(Datatype));
	p->top = 0;
	p->Capacity = 4;
}
void StackPush(Stack* p, Datatype x)
{
	assert(p);
	if (p->top == p->Capacity)  //检查是否要增容
	{
		p->a = (Datatype*)realloc(p->a, 2 * p->Capacity * sizeof(Datatype));
		p->Capacity = p->Capacity * 2;
	}
	p->a[p->top] = x;
	p->top++;
}
void StackPop(Stack* p)
{
	assert(p);
	if (p->top)
		p->top = p->top - 1;
}
void StackPrint(Stack* p)
{
	assert(p);
	for (int i = 0; i < p->top; i++)
	{
		printf(" %d ", p->a[i]);
	}
	printf("\n");
}
Datatype StackTop(Stack* p)
{
	return p->a[p->top - 1];
}
int StackEmpty(Stack* p)
{
	return p->top == 0;
}
void StackDestroy(Stack* p)
{
	free(p->a);
	p->a = NULL;
	p->top = 0;
	p->Capacity = 0;
}
//以上都是栈的基本操作，下面才是队列的实现
typedef struct {
	Stack s1;
	Stack s2;

} MyQueue;

/** Initialize your data structure here. */

MyQueue* myQueueCreate() {
	MyQueue* q=(MyQueue*)malloc(sizeof(MyQueue));
	StackInit(&(q->s1));
	StackInit(&(q->s2));
	return q;
}

/** Push element x to the back of queue. */
void myQueuePush(MyQueue* obj, int x) {
	int a = 0;
	StackPush(&(obj->s1), x);
}

/** Removes the element from in front of queue and returns that element. */
int myQueuePop(MyQueue* obj) {
	while (StackEmpty(&(obj->s1))==0)
	{
		StackPush(&(obj->s2), StackTop(&(obj->s1)));
		StackPop(&(obj->s1));
	}
	Datatype a = StackTop(&(obj->s2));
	StackPop(&(obj->s2));
	while (StackEmpty(&(obj->s2))==0)
	{
		StackPush(&(obj->s1), StackTop(&(obj->s2)));
		StackPop(&(obj->s2));
	}
	return a;

}

/** Get the front element. */
int myQueuePeek(MyQueue* obj) {
	while (StackEmpty(&(obj->s1)) == 0)
	{
		StackPush(&(obj->s2), StackTop(&(obj->s1)));
		StackPop(&(obj->s1));
	}
	Datatype a = StackTop(&(obj->s2));
	while (StackEmpty(&(obj->s2)) == 0)
	{
		StackPush(&(obj->s1), StackTop(&(obj->s2)));
		StackPop(&(obj->s2));
	}
	return a;


}

/** Returns whether the queue is empty. */
bool myQueueEmpty(MyQueue* obj) {
	return StackEmpty(&(obj->s1));

}

void myQueueFree(MyQueue* obj) {
	StackDestroy(&(obj->s1));
	StackDestroy(&(obj->s2));
	obj = NULL;
}

队列

队列的概念和结构

队列： 只允许在一段进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO（first in first out) 入队列、进行插入操作的一端称为队尾出队列、进行删除的一段称为队头
在这里插入图片描述

队列的实现

队列的实现同样可以使用数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>

typedef int DataType;
typedef struct BinaryTree
{
	DataType x;
	struct BinaryTree* _left;
	struct BinaryTree* _right;
}BT;

typedef BT* Datatype;
typedef struct ListNode
{
	Datatype x;
	struct ListNode* next;
}ListNode;

typedef struct Queue
{
	ListNode* head;
	ListNode* tail;
}Queue;

void QueueInit(Queue* q);  //初始化队列

void QueuePush(Queue* q, Datatype x);  // 入队

void QueuePop(Queue* q);    // 出队

Datatype QueueFront(Queue* q);  //输出队列队头的元素

Datatype QueueBack(Queue* q); // 输出队列队尾的元素
  
int QueueSize(Queue* q);    //输出队列的大小

int QueueEmpty(Queue* q);   //判断队列是否为空

void QueueDestroy(Queue* q);   //队列销毁

以上时栈的结构和具体的基本操作

下面是这些具体操作的实现

#define _CRT_SECURE_NO_WARNINGS 1

#include"Queue.h"

void QueueInit(Queue* q)
{
	ListNode* First = (ListNode*)malloc(sizeof(ListNode));
	q->head = q->tail = First;
	q->tail->next = NULL;
}

void QueuePush(Queue* q, Datatype x)
{
	assert(q);
	q->tail->x = x;
	ListNode* NewNode = (ListNode*)malloc(sizeof(ListNode));
	q->tail->next = NewNode;
	q->tail = NewNode;
	q->tail->next = NULL;
}

void QueuePop(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	if (!QueueEmpty(q))
	{
		ListNode* temp = q->head->next;
		free(q->head);
		q->head = temp;
	}

}

Datatype QueueFront(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->head->x;
}

Datatype QueueBack(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	ListNode* cur = q->head;
	while (cur->next != q->tail)
	{
		cur = cur->next;
	}
	return cur->x;
}

int QueueSize(Queue* q)
{
	if (QueueEmpty(q))
	{
		return 0;
	}
	ListNode* cur = q->head;
	int k = 0;
	while (cur != q->tail)
	{
		cur = cur->next;
		k++;
	}
	return k;
}

int QueueEmpty(Queue* q)
{
	return q->head == q->tail;
}

void QueueDestroy(Queue* q)
{
	ListNode* cur = q->head;
	while (cur != q->tail)
	{
		ListNode* temp = cur->next;
		free(cur);
		cur = temp;
	}
	free(cur);
	cur = NULL;
	q->head = NULL;
	q->tail = NULL;

}

队列的应用

用队列实现栈

leetcode——原题
实现思路： 用两个队列来实现栈的功能，栈用队列的实现不同主要在myStackPop这个函数上，该如何得到队尾的元素是本题的难点：
在这里插入图片描述

以上就是我处理的思路：

首先保证q1永远是储存数据的队列，而q2是一个用来导数据的空队列
将q1中n-1个元素分别拷入q2，并将其出队列，留下队尾元素（栈顶），将其出队列（换句话就是将q1除队尾的元素拷入q2，并删除）
将q1与q2交换

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>



typedef int Datatype;
typedef struct listNode
{
	Datatype x;
	struct listNode* next;
}ListNode;

typedef struct
{
	ListNode* head;
	ListNode* tail;
}Queue;

void QueueInit(Queue* q)
{
	ListNode* First = (ListNode*)malloc(sizeof(ListNode));
	First->next = NULL;
	q->head = q->tail = First;
	q->tail->next = NULL;
}
int QueueEmpty(Queue* q)
{
	return q->head == q->tail;
}
void QueuePush(Queue* q, Datatype x)
{
	assert(q);
	q->tail->x = x;
	ListNode* NewNode = (ListNode*)malloc(sizeof(ListNode));
	q->tail->next = NewNode;
	q->tail = NewNode;
	q->tail->next = NULL;
}

void QueuePop(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	if (!QueueEmpty(q))
	{
		ListNode* temp = q->head->next;
		free(q->head);
		q->head = temp;
	}

}

Datatype QueueFront(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->head->x;
}

Datatype QueueBack(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	ListNode* cur = q->head;
	while (cur->next != q->tail)
	{
		cur = cur->next;
	}
	return cur->x;
}

int QueueSize(Queue* q)
{
	if (QueueEmpty(q))
	{
		return 0;
	}
	ListNode* cur = q->head;
	int k = 0;
	while (cur != q->tail)
	{
		cur = cur->next;
		k++;
	}
	return k;
}



void QueueDestroy(Queue* q)
{
	ListNode* cur = q->head;
	while (cur != q->tail)
	{
		ListNode* temp = cur->next;
		free(cur);
		cur = temp;
	}
	free(cur);
	cur = NULL;
	q->head = NULL;
	q->tail = NULL;

}
void check(Queue* q1, Queue* q2)
{
	if (QueueEmpty(q1)) {
		Queue temp = *q1;
		*q1 = *q2;
		*q2 = temp;
	}
}

typedef struct {
	Queue q1;
	Queue q2;
} MyStack;

/** Initialize your data structure here. */

MyStack* myStackCreate() {
	MyStack* p = (MyStack*)malloc(sizeof(MyStack));
	QueueInit(&(p->q1));
	QueueInit(&(p->q2));
	return p;

}

/** Push element x onto stack. */
void myStackPush(MyStack* obj, int x) {
	check(&(obj->q1), &(obj->q2));
	QueuePush(&(obj->q1), x);
}

/** Removes the element on top of the stack and returns that element. */
int myStackPop(MyStack* obj) {
	check(&(obj->q1), &(obj->q2));
	int b = 0;
	while (!QueueEmpty(&(obj->q1)))
	{
		if (QueueSize(&(obj->q1)) == 1)
		{
			b = QueueFront(&(obj->q1));
			QueuePop(&(obj->q1));
			continue;
		}
		int a = QueueFront(&(obj->q1));
		QueuePop(&(obj->q1));
		QueuePush(&(obj->q2), a);

	}

	return b;
}

/** Get the top element. */
int myStackTop(MyStack* obj) {
	check(&(obj->q1), &(obj->q2));
	return QueueBack(&(obj->q1));

}

/** Returns whether the stack is empty. */
bool myStackEmpty(MyStack* obj) {
	check(&(obj->q1), &(obj->q2));
	return QueueEmpty(&(obj->q1));

}

void myStackFree(MyStack* obj) {
	QueueDestroy(&(obj->q1));
	QueueDestroy(&(obj->q2));
	free(obj);
}

循环队列

leetcode——原题

循环队列的逻辑结构

循环队列由一个队头（Front）偏移量和一个和一个队尾偏移量（Rear）和一个顺序表组成，在逻辑上是一个环形结构。但在物理存储结构上实际是一个顺序表，靠着一定的条件使得Front和Rear偏移量循环遍历数组。
逻辑结构：
在这里插入图片描述
实际上的物理结构：

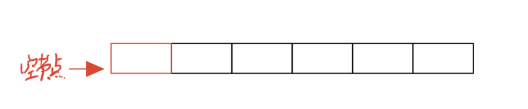
在这里插入图片描述

结构设计

如何判断队列空或队列的满
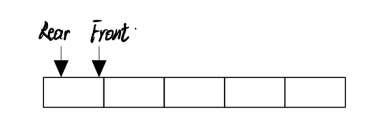
在这里插入图片描述

如果我们仔细思考一下就会发现队空和队满两种情况都是Rear和Front都是重合的，如果用Rear==Front就无法判断队空和队满
于是我们就用添加一个多余的空间（K+1）来解决这个问题
在这里插入图片描述

当Rear==Front时，这时我们就认为循环队列是空的

在这里插入图片描述
由于Rear始终指向的是队尾元素的下一个空间，所以设置一个空节点使队满的时候，Rear和Front不重合但是，满足条件Rear+1==Front，但是这里的判断条件实际上在写的过程中要写成((obj->Rear+1)%(obj->capacity))==obj->Front因为Rear+1可能要越过数组，所以要将他返回数组的起点以达到循环。

typedef struct {
    int *a;
    int Front;
    int Rear;
    int capacity;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue*q=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    q->a=(int *)malloc((k+1)*sizeof(int));
    q->Front=0;
    q->Rear=0;
    q->capacity=k+1;
    return q;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return ((obj->Rear+1)%(obj->capacity))==obj->Front;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return ((obj->Front)%(obj->capacity))==obj->Rear;

}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))  //检查队列是否满了
    return false;
    obj->a[obj->Rear]=value;
    obj->Rear++;
    obj->Rear%=obj->capacity;
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    return false;
    obj->Front++;
    obj->Front%=obj->capacity;
    return true;
}


int myCircularQueueFront(MyCircularQueue* obj) {

    if(myCircularQueueIsEmpty(obj))
    return -1;
    return obj->a[obj->Front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
     if(myCircularQueueIsEmpty(obj))
    return -1;

    return obj->a[(obj->Rear - 1+obj->capacity)%obj->capacity]; 
}




void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
    obj=NULL;

}

易错点！

下面来分享一下我在写这个oj的时候遇到的问题：

首先是在myCircularQueueFront和myCircularQueueRear函数里面没有判断循环链表是否为空
第二个问题我找了好久才发现myCircularQueueRear返回的是队尾的数值，由于Rear始终指向的是下一个节点，所以末尾的元素是a[(obj->Rear - 1] 但是在这里要判断Rear-1是否满足循环数组的要求，如果不检查就会一直报heap—overflow