[数据结构与算法]动态规划学习

一、动态规划学习

动态规划来源于运筹学，是求解决策过程最优化的一种数学方法。在20世纪50年代初美国数学家R. E.
Bellman等提出的最优化原理，动态规划的核心思想是利用各阶段之间的关系，逐个求解，最终得到全局最优解。

设计一个动态规划算法的关键点是确认原问题与子问题、动态规划的状态、边界状态值和状态转移方程等。尤其是状态转移方程特别重要，状态转移方程得不到，整个算法就进行不下去。

二、动态规划解题步骤

1. 想清楚原问题与子问题
2. 设计状态
3. 设计状态转移方程
4. 确定边界状态值

三、动态规划的性质

3.1 最优子结构

• 如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。
• 最优子结构性质为动态规划算法解决问题提供了重要线索。

3.2 重复子问题

• 求解原问题时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。
• 动态规划算法利用了重复子问题的性质，对每一个子问题只计算一次，将结果加入备忘录
• 当再次需要计算已经计算过的子问题时，只需查找备忘录，从而获得较高的效率。

3.3 无后效性

• 子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。

3.4 动态规划的求解方向

1. 自底向上（递推）
2. 自顶向下（递归）

四、动态规划示例-爬楼梯

4.1 题目描述

在爬楼梯的时候，每次可以往上爬1阶台阶或2阶台阶，问n阶楼梯有多少种上楼的方式？

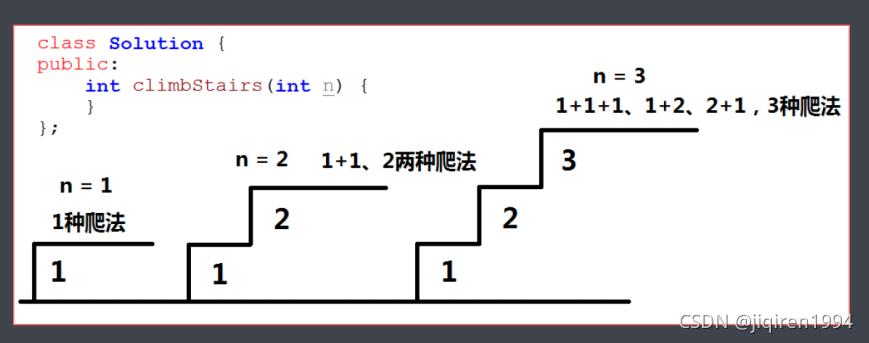
4.2 暴力解法

• 暴力解法中可以使用递归算法
• 如下图，4的爬法=3的爬法+2的爬法，从而可以得到递归的核心公式
  

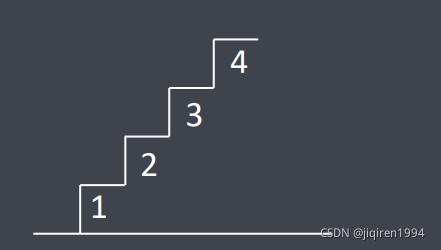
class Solution {
	public int climbStairs(int n){
		if(n == 1 || n == 2){
			return n;
		}
		return climbStairs(n-1) + climbStairs(n-2);
	}
}

4.3 动态规划解法

class Solution {
public int climbStairs(int n){
	// 注意构建n+3的数组来处理n=0,1,2的特殊情况
	int[] dp= new int[n+3];
	// 确定状态数组的前几个元素初值
	dp[1]=1;
	dp[2]=2;
	// 利用状态转移方程逐步求解最优解
	for(int i=3;i<=n;i++){
		dp[i]=dp[i-1]+dp[i-2];
	}
	return dp[n];
}
}