题目一
https://leetcode.com/problems/burst-balloons/
打爆气球的最大得分
?尝试:int f(L,R) 设计的f()函数必须满足,在arr L....R 上打爆气球最大得分,必须满足L-1,R+1没爆的情况下,才能调用这个函数去计算打爆L....R上的所有气球的最大得分
public static int maxCoins0(int[] arr) {
// [3,2,1,3]
// [1,3,2,1,3,1]
int N = arr.length;
int[] help = new int[N + 2];
for (int i = 0; i < N; i++) {
help[i + 1] = arr[i];
}
help[0] = 1;
help[N + 1] = 1;
return func(help, 1, N);
}
// L-1位置,和R+1位置,永远不越界,并且,[L-1] 和 [R+1] 一定没爆呢!
// 返回,arr[L...R]打爆所有气球,最大得分是什么
public static int func(int[] arr, int L, int R) {
if (L == R) {
return arr[L - 1] * arr[L] * arr[R + 1];
}
// 尝试每一种情况,最后打爆的气球,是什么位置
// L...R
// L位置的气球,最后打爆
int max = func(arr, L + 1, R) + arr[L - 1] * arr[L] * arr[R + 1];
// R位置的气球,最后打爆
max = Math.max(max, func(arr, L, R - 1) + arr[L - 1] * arr[R] * arr[R + 1]);
// 尝试所有L...R,中间的位置,(L,R)
for (int i = L + 1; i < R; i++) {
// i位置的气球,最后打爆
int left = func(arr, L, i - 1);
int right = func(arr, i + 1, R);
int last = arr[L - 1] * arr[i] * arr[R + 1];
int cur = left + right + last;
max = Math.max(max, cur);
}
return max;
}public static int maxCoins1(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
if (arr.length == 1) {
return arr[0];
}
int N = arr.length;
int[] help = new int[N + 2];
help[0] = 1;
help[N + 1] = 1;
for (int i = 0; i < N; i++) {
help[i + 1] = arr[i];
}
return process(help, 1, N);
}
// 打爆arr[L..R]范围上的所有气球,返回最大的分数
// 假设arr[L-1]和arr[R+1]一定没有被打爆
public static int process(int[] arr, int L, int R) {
if (L == R) {// 如果arr[L..R]范围上只有一个气球,直接打爆即可
return arr[L - 1] * arr[L] * arr[R + 1];
}
// 最后打爆arr[L]的方案,和最后打爆arr[R]的方案,先比较一下
int max = Math.max(arr[L - 1] * arr[L] * arr[R + 1] + process(arr, L + 1, R),
arr[L - 1] * arr[R] * arr[R + 1] + process(arr, L, R - 1));
// 尝试中间位置的气球最后被打爆的每一种方案
for (int i = L + 1; i < R; i++) {
max = Math.max(max, arr[L - 1] * arr[i] * arr[R + 1] + process(arr, L, i - 1) + process(arr, i + 1, R));
}
return max;
}public static int maxCoins2(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
if (arr.length == 1) {
return arr[0];
}
int N = arr.length;
int[] help = new int[N + 2];
help[0] = 1;
help[N + 1] = 1;
for (int i = 0; i < N; i++) {
help[i + 1] = arr[i];
}
int[][] dp = new int[N + 2][N + 2];
for (int i = 1; i <= N; i++) {
dp[i][i] = help[i - 1] * help[i] * help[i + 1];
}
for (int L = N; L >= 1; L--) {
for (int R = L + 1; R <= N; R++) {
int ans = help[L - 1] * help[L] * help[R + 1] + dp[L + 1][R];
ans = Math.max(ans, help[L - 1] * help[R] * help[R + 1] + dp[L][R - 1]);
for (int i = L + 1; i < R; i++) {
ans = Math.max(ans, help[L - 1] * help[i] * help[R + 1] + dp[L][i - 1] + dp[i + 1][R]);
}
dp[L][R] = ans;
}
}
return dp[1][N];
}题目二
https://leetcode.com/problems/remove-boxes/
移动盒子
简化外部条件:arr L....R上去消最大得分,它前面有k个和L位置一样的数在它左边的情况下,最大得分是多少
// arr[L...R]消除,而且前面跟着K个arr[L]这个数
// 返回:所有东西都消掉,最大得分
public static int func1(int[] arr, int L, int R, int K) {
if (L > R) {
return 0;
}
int ans = func1(arr, L + 1, R, 0) + (K + 1) * (K + 1);
// 前面的K个X,和arr[L]数,合在一起了,现在有K+1个arr[L]位置的数
for (int i = L + 1; i <= R; i++) {
if (arr[i] == arr[L]) {
ans = Math.max(ans, func1(arr, L + 1, i - 1, 0) + func1(arr, i, R, K + 1));
}
}
return ans;
}public static int removeBoxes1(int[] boxes) {
int N = boxes.length;
int[][][] dp = new int[N][N][N];
int ans = process1(boxes, 0, N - 1, 0, dp);
return ans;
}
public static int process1(int[] boxes, int L, int R, int K, int[][][] dp) {
if (L > R) {
return 0;
}
if (dp[L][R][K] > 0) {
return dp[L][R][K];
}
int ans = process1(boxes, L + 1, R, 0, dp) + (K + 1) * (K + 1);
for (int i = L + 1; i <= R; i++) {
if (boxes[i] == boxes[L]) {
ans = Math.max(ans, process1(boxes, L + 1, i - 1, 0, dp) + process1(boxes, i, R, K + 1, dp));
}
}
dp[L][R][K] = ans;
return ans;
}public static int removeBoxes2(int[] boxes) {
int N = boxes.length;
int[][][] dp = new int[N][N][N];
int ans = process2(boxes, 0, N - 1, 0, dp);
return ans;
}
public static int process2(int[] boxes, int L, int R, int K, int[][][] dp) {
if (L > R) {
return 0;
}
if (dp[L][R][K] > 0) {
return dp[L][R][K];
}
// 找到开头,
// 1,1,1,1,1,5
// 3 4 5 6 7 8
// !
int last = L;
while (last + 1 <= R && boxes[last + 1] == boxes[L]) {
last++;
}
// K个1 (K + last - L) last
int pre = K + last - L;
int ans = (pre + 1) * (pre + 1) + process2(boxes, last + 1, R, 0, dp);
for (int i = last + 2; i <= R; i++) {
if (boxes[i] == boxes[L] && boxes[i - 1] != boxes[L]) {
ans = Math.max(ans, process2(boxes, last + 1, i - 1, 0, dp) + process2(boxes, i, R, pre + 1, dp));
}
}
dp[L][R][K] = ans;
return ans;
}题目三
如果一个字符相邻的位置没有相同字符,那么这个位置的字符出现不能被消掉。比如:"ab",其中a和b都不能被消掉
如果一个字符相邻的位置有相同字符,就可以一起消掉。比如:“abbbc”,中间一串的b是可以被消掉的,
消除之后剩下“ac”。某些字符如果消掉了,剩下的字符认为重新靠在一起
给定一个字符串,你可以决定每一步消除的顺序,目标是请尽可能多的消掉字符,返回最少的剩余字符数量
比如:"aacca", 如果先消掉最左侧的"aa",那么将剩下"cca",然后把"cc"消掉,剩下的"a"将无法再消除,返回1
但是如果先消掉中间的"cc",那么将剩下"aaa",最后都消掉就一个字符也不剩了,返回0,这才是最优解。
再比如:"baaccabb",如果先消除最左侧的两个a,剩下"bccabb",如果再消除最左侧的两个c,剩下"babb",
最后消除最右侧的两个b,剩下"ba"无法再消除,返回2
而最优策略是:先消除中间的两个c,剩下"baaabb",再消除中间的三个a,剩下"bbb",最后消除三个b,
不留下任何字符,返回0,这才是最优解
字符消除游戏
f(L,R,K)
arr L....R 消除的情况下,最少能剩几个字符,前面跟着k个和L一样的字符,事实上只需要知道前面有没有L位置的数跟着就可以,不需要知道几个,所以bool类型就够了
// 暴力解
public static int restMin1(String s) {
if (s == null) {
return 0;
}
if (s.length() < 2) {
return s.length();
}
int minLen = s.length();
for (int L = 0; L < s.length(); L++) {
for (int R = L + 1; R < s.length(); R++) {
if (canDelete(s.substring(L, R + 1))) {
minLen = Math.min(minLen, restMin1(s.substring(0, L) + s.substring(R + 1, s.length())));
}
}
}
return minLen;
}
public static boolean canDelete(String s) {
char[] str = s.toCharArray();
for (int i = 1; i < str.length; i++) {
if (str[i - 1] != str[i]) {
return false;
}
}
return true;
}// 优良尝试的暴力递归版本
public static int restMin2(String s) {
if (s == null) {
return 0;
}
if (s.length() < 2) {
return s.length();
}
char[] str = s.toCharArray();
return process(str, 0, str.length - 1, false);
}
// str[L...R] 前面有没有跟着[L]字符,has T 有 F 无
// L,R,has
// 最少能剩多少字符,消不了
public static int process(char[] str, int L, int R, boolean has) {
if (L > R) {
return 0;
}
if (L == R) {
return has ? 0 : 1;
}
int index = L;
int K = has ? 1 : 0;
while (index <= R && str[index] == str[L]) {
K++;
index++;
}
// index表示,第一个不是[L]字符的位置
int way1 = (K > 1 ? 0 : 1) + process(str, index, R, false);
int way2 = Integer.MAX_VALUE;
for (int split = index; split <= R; split++) {
if (str[split] == str[L] && str[split] != str[split - 1]) {
if (process(str, index, split - 1, false) == 0) {
way2 = Math.min(way2, process(str, split, R, K != 0));
}
}
}
return Math.min(way1, way2);
}// 优良尝试的动态规划版本
public static int restMin3(String s) {
if (s == null) {
return 0;
}
if (s.length() < 2) {
return s.length();
}
char[] str = s.toCharArray();
int N = str.length;
int[][][] dp = new int[N][N][2];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
for (int k = 0; k < 2; k++) {
dp[i][j][k] = -1;
}
}
}
return dpProcess(str, 0, N - 1, false, dp);
}
public static int dpProcess(char[] str, int L, int R, boolean has, int[][][] dp) {
if (L > R) {
return 0;
}
int K = has ? 1 : 0;
if (dp[L][R][K] != -1) {
return dp[L][R][K];
}
int ans = 0;
if (L == R) {
ans = (K == 0 ? 1 : 0);
} else {
int index = L;
int all = K;
while (index <= R && str[index] == str[L]) {
all++;
index++;
}
int way1 = (all > 1 ? 0 : 1) + dpProcess(str, index, R, false, dp);
int way2 = Integer.MAX_VALUE;
for (int split = index; split <= R; split++) {
if (str[split] == str[L] && str[split] != str[split - 1]) {
if (dpProcess(str, index, split - 1, false, dp) == 0) {
way2 = Math.min(way2, dpProcess(str, split, R, all > 0, dp));
}
}
}
ans = Math.min(way1, way2);
}
dp[L][R][K] = ans;
return ans;
}题目四
给定一个数组arr,和一个正数M,
返回在arr的子数组在长度不超过M的情况下,最大的累加和
解题:数组处理成前缀和数组,然后使用窗口内最大值更新结构
// O(N^2)的解法,暴力解,用作对数器
public static int test(int[] arr, int M) {
if (arr == null || arr.length == 0 || M < 1) {
return 0;
}
int N = arr.length;
int max = Integer.MIN_VALUE;
for (int L = 0; L < N; L++) {
int sum = 0;
for (int R = L; R < N; R++) {
if (R - L + 1 > M) {
break;
}
sum += arr[R];
max = Math.max(max, sum);
}
}
return max;
} // O(N)的解法,最优解
public static int maxSum(int[] arr, int M) {
if (arr == null || arr.length == 0 || M < 1) {
return 0;
}
int N = arr.length;
int[] sum = new int[N];
sum[0] = arr[0];
for (int i = 1; i < N; i++) {
sum[i] = sum[i - 1] + arr[i];
}
LinkedList<Integer> qmax = new LinkedList<>();
int i = 0;
int end = Math.min(N, M);
for (; i < end; i++) {
while (!qmax.isEmpty() && sum[qmax.peekLast()] <= sum[i]) {
qmax.pollLast();
}
qmax.add(i);
}
int max = sum[qmax.peekFirst()];
int L = 0;
for (; i < N; L++, i++) {
if (qmax.peekFirst() == L) {
qmax.pollFirst();
}
while (!qmax.isEmpty() && sum[qmax.peekLast()] <= sum[i]) {
qmax.pollLast();
}
qmax.add(i);
max = Math.max(max, sum[qmax.peekFirst()] - sum[L]);
}
for (; L < N - 1; L++) {
if (qmax.peekFirst() == L) {
qmax.pollFirst();
}
max = Math.max(max, sum[qmax.peekFirst()] - sum[L]);
}
return max;
}题目五
哈夫曼树详解
分金条问题
解题:所有数建立小根堆,弹出两个较小的值,生成一个和再扔进小根堆,如此反复
哈夫曼数
// 根据文章str, 生成词频统计表
public static HashMap<Character, Integer> countMap(String str) {
HashMap<Character, Integer> ans = new HashMap<>();
char[] s = str.toCharArray();
for (char cha : s) {
if (!ans.containsKey(cha)) {
ans.put(cha, 1);
} else {
ans.put(cha, ans.get(cha) + 1);
}
}
return ans;
}
public static class Node {
public int count;
public Node left;
public Node right;
public Node(int c) {
count = c;
}
}
public static class NodeComp implements Comparator<Node> {
@Override
public int compare(Node o1, Node o2) {
return o1.count - o2.count;
}
}
// 根据由文章生成词频表countMap,生成哈夫曼编码表
// key : 字符
// value: 该字符编码后的二进制形式
// 比如,频率表 A:60, B:45, C:13 D:69 E:14 F:5 G:3
// A 10
// B 01
// C 0011
// D 11
// E 000
// F 00101
// G 00100
public static HashMap<Character, String> huffmanForm(HashMap<Character, Integer> countMap) {
HashMap<Character, String> ans = new HashMap<>();
if (countMap.size() == 1) {
for (char key : countMap.keySet()) {
ans.put(key, "0");
}
return ans;
}
HashMap<Node, Character> nodes = new HashMap<>();
PriorityQueue<Node> heap = new PriorityQueue<>(new NodeComp());
for (Entry<Character, Integer> entry : countMap.entrySet()) {
Node cur = new Node(entry.getValue());
char cha = entry.getKey();
nodes.put(cur, cha);
heap.add(cur);
}
while (heap.size() != 1) {
Node a = heap.poll();
Node b = heap.poll();
Node h = new Node(a.count + b.count);
h.left = a;
h.right = b;
heap.add(h);
}
Node head = heap.poll();
fillForm(head, "", nodes, ans);
return ans;
}
public static void fillForm(Node head, String pre, HashMap<Node, Character> nodes, HashMap<Character, String> ans) {
if (nodes.containsKey(head)) {
ans.put(nodes.get(head), pre);
} else {
fillForm(head.left, pre + "0", nodes, ans);
fillForm(head.right, pre + "1", nodes, ans);
}
}
// 原始字符串str,根据哈夫曼编码表,转译成哈夫曼编码返回
public static String huffmanEncode(String str, HashMap<Character, String> huffmanForm) {
char[] s = str.toCharArray();
StringBuilder builder = new StringBuilder();
for (char cha : s) {
builder.append(huffmanForm.get(cha));
}
return builder.toString();
}
// 原始字符串的哈夫曼编码huffmanEncode,根据哈夫曼编码表,还原成原始字符串
public static String huffmanDecode(String huffmanEncode, HashMap<Character, String> huffmanForm) {
TrieNode root = createTrie(huffmanForm);
TrieNode cur = root;
char[] encode = huffmanEncode.toCharArray();
StringBuilder builder = new StringBuilder();
for (int i = 0; i < encode.length; i++) {
int index = encode[i] == '0' ? 0 : 1;
cur = cur.nexts[index];
if (cur.nexts[0] == null && cur.nexts[1] == null) {
builder.append(cur.value);
cur = root;
}
}
return builder.toString();
}
public static TrieNode createTrie(HashMap<Character, String> huffmanForm) {
TrieNode root = new TrieNode();
for (char key : huffmanForm.keySet()) {
char[] path = huffmanForm.get(key).toCharArray();
TrieNode cur = root;
for (int i = 0; i < path.length; i++) {
int index = path[i] == '0' ? 0 : 1;
if (cur.nexts[index] == null) {
cur.nexts[index] = new TrieNode();
}
cur = cur.nexts[index];
}
cur.value = key;
}
return root;
}
public static class TrieNode {
public char value;
public TrieNode[] nexts;
public TrieNode() {
value = 0;
nexts = new TrieNode[2];
}
}
题目六
https://leetcode.com/problems/strange-printer/
奇怪打印机(范围上尝试模型)
第一种可能:L...L范围上刷完是a;L+1到R上刷完是b;总数a+b
第二种可能:L...L+1范围上刷完是c;L+2到R上刷完是d;总数c+d.....
public static int strangePrinter1(String s) {
if (s == null || s.length() == 0) {
return 0;
}
char[] str = s.toCharArray();
return process1(str, 0, str.length - 1);
}
// 要想刷出str[L...R]的样子!
// 返回最少的转数
public static int process1(char[] str, int L, int R) {
if (L == R) {
return 1;
}
// L...R
int ans = R - L + 1;
for (int k = L + 1; k <= R; k++) {
// L...k-1 k....R
ans = Math.min(ans, process1(str, L, k - 1) + process1(str, k, R) - (str[L] == str[k] ? 1 : 0));
}
return ans;
}public static int strangePrinter2(String s) {
if (s == null || s.length() == 0) {
return 0;
}
char[] str = s.toCharArray();
int N = str.length;
int[][] dp = new int[N][N];
return process2(str, 0, N - 1, dp);
}
public static int process2(char[] str, int L, int R, int[][] dp) {
if (dp[L][R] != 0) {
return dp[L][R];
}
int ans = R - L + 1;
if (L == R) {
ans = 1;
} else {
for (int k = L + 1; k <= R; k++) {
ans = Math.min(ans, process2(str, L, k - 1, dp) + process2(str, k, R, dp) - (str[L] == str[k] ? 1 : 0));
}
}
dp[L][R] = ans;
return ans;
}public static int strangePrinter3(String s) {
if (s == null || s.length() == 0) {
return 0;
}
char[] str = s.toCharArray();
int N = str.length;
int[][] dp = new int[N][N];
dp[N - 1][N - 1] = 1;
for (int i = 0; i < N - 1; i++) {
dp[i][i] = 1;
dp[i][i + 1] = str[i] == str[i + 1] ? 1 : 2;
}
for (int L = N - 3; L >= 0; L--) {
for (int R = L + 2; R < N; R++) {
dp[L][R] = R - L + 1;
for (int k = L + 1; k <= R; k++) {
dp[L][R] = Math.min(dp[L][R], dp[L][k - 1] + dp[k][R] - (str[L] == str[k] ? 1 : 0));
}
}
}
return dp[0][N - 1];
}题目七
整型数组arr长度为n(3 <= n <= 10^4),最初每个数字是<=200的正数且满足如下条件:
1. arr[0] <= arr[1]
2.arr[n-1] <= arr[n-2]
3. arr[i] <= max(arr[i-1], arr[i+1])
但是在arr有些数字丢失了,比如k位置的数字之前是正数,
丢失之后k位置的数字为0。
请你根据上述条件, 计算可能有多少种不同的arr可以满足以上条件。
比如 [6,0,9] 只有还原成 [6,9,9]满足全部三个条件,所以返回1种。
外部信息简化:
public static int ways0(int[] arr) {
return process0(arr, 0);
}
public static int process0(int[] arr, int index) {
if (index == arr.length) {
return isValid(arr) ? 1 : 0;
} else {
if (arr[index] != 0) {
return process0(arr, index + 1);
} else {
int ways = 0;
for (int v = 1; v < 201; v++) {
arr[index] = v;
ways += process0(arr, index + 1);
}
arr[index] = 0;
return ways;
}
}
}
public static boolean isValid(int[] arr) {
if (arr[0] > arr[1]) {
return false;
}
if (arr[arr.length - 1] > arr[arr.length - 2]) {
return false;
}
for (int i = 1; i < arr.length - 1; i++) {
if (arr[i] > Math.max(arr[i - 1], arr[i + 1])) {
return false;
}
}
return true;
}public static int ways1(int[] arr) {
int N = arr.length;
if (arr[N - 1] != 0) {
return process1(arr, N - 1, arr[N - 1], 2);
} else {
int ways = 0;
for (int v = 1; v < 201; v++) {
ways += process1(arr, N - 1, v, 2);
}
return ways;
}
}
// 如果i位置的数字变成了v,
// 并且arr[i]和arr[i+1]的关系为s,
// s==0,代表arr[i] < arr[i+1] 右大
// s==1,代表arr[i] == arr[i+1] 右=当前
// s==2,代表arr[i] > arr[i+1] 右小
// 返回0...i范围上有多少种有效的转化方式?
public static int process1(int[] arr, int i, int v, int s) {
if (i == 0) { // 0...i 只剩一个数了,0...0
return ((s == 0 || s == 1) && (arr[0] == 0 || v == arr[0])) ? 1 : 0;
}
// i > 0
if (arr[i] != 0 && v != arr[i]) {
return 0;
}
// i>0 ,并且, i位置的数真的可以变成V,
int ways = 0;
if (s == 0 || s == 1) { // [i] -> V <= [i+1]
for (int pre = 1; pre < 201; pre++) {
ways += process1(arr, i - 1, pre, pre < v ? 0 : (pre == v ? 1 : 2));
}
} else { // ? 当前 > 右 当前 <= max{左,右}
for (int pre = v; pre < 201; pre++) {
ways += process1(arr, i - 1, pre, pre == v ? 1 : 2);
}
}
return ways;
}public static int zuo(int[] arr, int i, int v, int s) {
if (i == 0) { // 0...i 只剩一个数了,0...0
return ((s == 0 || s == 1) && (arr[0] == 0 || v == arr[0])) ? 1 : 0;
}
// i > 0
if (arr[i] != 0 && v != arr[i]) {
return 0;
}
// i>0 ,并且, i位置的数真的可以变成V,
int ways = 0;
if (s == 0 || s == 1) { // [i] -> V <= [i+1]
for (int pre = 1; pre < v; pre++) {
ways += zuo(arr, i - 1, pre, 0);
}
}
ways += zuo(arr, i - 1, v, 1);
for (int pre = v + 1; pre < 201; pre++) {
ways += zuo(arr, i - 1, pre, 2);
}
return ways;
}public static int ways2(int[] arr) {
int N = arr.length;
int[][][] dp = new int[N][201][3];
if (arr[0] != 0) {
dp[0][arr[0]][0] = 1;
dp[0][arr[0]][1] = 1;
} else {
for (int v = 1; v < 201; v++) {
dp[0][v][0] = 1;
dp[0][v][1] = 1;
}
}
for (int i = 1; i < N; i++) {
for (int v = 1; v < 201; v++) {
for (int s = 0; s < 3; s++) {
if (arr[i] == 0 || v == arr[i]) {
if (s == 0 || s == 1) {
for (int pre = 1; pre < v; pre++) {
dp[i][v][s] += dp[i - 1][pre][0];
}
}
dp[i][v][s] += dp[i - 1][v][1];
for (int pre = v + 1; pre < 201; pre++) {
dp[i][v][s] += dp[i - 1][pre][2];
}
}
}
}
}
if (arr[N - 1] != 0) {
return dp[N - 1][arr[N - 1]][2];
} else {
int ways = 0;
for (int v = 1; v < 201; v++) {
ways += dp[N - 1][v][2];
}
return ways;
}
}public static int ways3(int[] arr) {
int N = arr.length;
int[][][] dp = new int[N][201][3];
if (arr[0] != 0) {
dp[0][arr[0]][0] = 1;
dp[0][arr[0]][1] = 1;
} else {
for (int v = 1; v < 201; v++) {
dp[0][v][0] = 1;
dp[0][v][1] = 1;
}
}
int[][] presum = new int[201][3];
for (int v = 1; v < 201; v++) {
for (int s = 0; s < 3; s++) {
presum[v][s] = presum[v - 1][s] + dp[0][v][s];
}
}
for (int i = 1; i < N; i++) {
for (int v = 1; v < 201; v++) {
for (int s = 0; s < 3; s++) {
if (arr[i] == 0 || v == arr[i]) {
if (s == 0 || s == 1) {
dp[i][v][s] += sum(1, v - 1, 0, presum);
}
dp[i][v][s] += dp[i - 1][v][1];
dp[i][v][s] += sum(v + 1, 200, 2, presum);
}
}
}
for (int v = 1; v < 201; v++) {
for (int s = 0; s < 3; s++) {
presum[v][s] = presum[v - 1][s] + dp[i][v][s];
}
}
}
if (arr[N - 1] != 0) {
return dp[N - 1][arr[N - 1]][2];
} else {
return sum(1, 200, 2, presum);
}
}
public static int sum(int begin, int end, int relation, int[][] presum) {
return presum[end][relation] - presum[begin - 1][relation];
}题目八
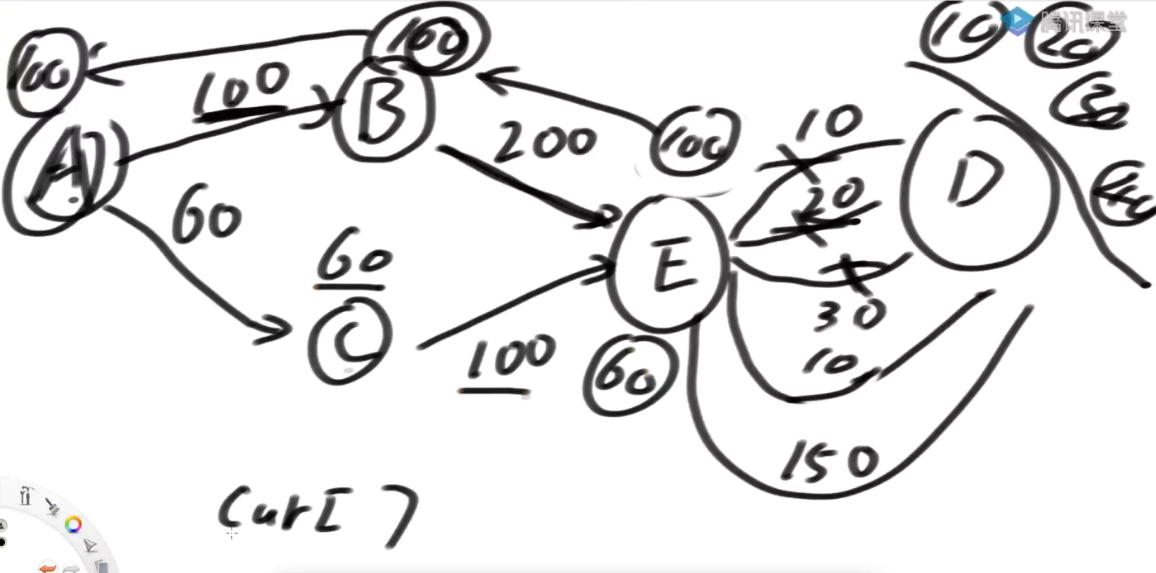
最大网络流算法之dinic算法详解
1.含有一个负反馈路线
public static class Edge {
public int from;
public int to;
public int available;
public Edge(int a, int b, int c) {
from = a;
to = b;
available = c;
}
}
public static class Dinic {
private int N;
private ArrayList<ArrayList<Integer>> nexts;
private ArrayList<Edge> edges;
private int[] depth;
private int[] cur;
public Dinic(int nums) {
N = nums + 1;
nexts = new ArrayList<>();
for (int i = 0; i <= N; i++) {
nexts.add(new ArrayList<>());
}
edges = new ArrayList<>();
depth = new int[N];
cur = new int[N];
}
public void addEdge(int u, int v, int r) {
int m = edges.size();
edges.add(new Edge(u, v, r));
nexts.get(u).add(m);
edges.add(new Edge(v, u, 0));
nexts.get(v).add(m + 1);
}
public int maxFlow(int s, int t) {
int flow = 0;
while (bfs(s, t)) {
Arrays.fill(cur, 0);
flow += dfs(s, t, Integer.MAX_VALUE);
Arrays.fill(depth, 0);
}
return flow;
}
private boolean bfs(int s, int t) {
LinkedList<Integer> queue = new LinkedList<>();
queue.addFirst(s);
boolean[] visited = new boolean[N];
visited[s] = true;
while (!queue.isEmpty()) {
int u = queue.pollLast();
for (int i = 0; i < nexts.get(u).size(); i++) {
Edge e = edges.get(nexts.get(u).get(i));
int v = e.to;
if (!visited[v] && e.available > 0) {
visited[v] = true;
depth[v] = depth[u] + 1;
if (v == t) {
break;
}
queue.addFirst(v);
}
}
}
return visited[t];
}
// 当前来到了s点,s可变
// 最终目标是t,t固定参数
// r,收到的任务
// 收集到的流,作为结果返回,ans <= r
private int dfs(int s, int t, int r) {
if (s == t || r == 0) {
return r;
}
int f = 0;
int flow = 0;
// s点从哪条边开始试 -> cur[s]
for (; cur[s] < nexts.get(s).size(); cur[s]++) {
int ei = nexts.get(s).get(cur[s]);
Edge e = edges.get(ei);
Edge o = edges.get(ei ^ 1);
if (depth[e.to] == depth[s] + 1 && (f = dfs(e.to, t, Math.min(e.available, r))) != 0) {
e.available -= f;
o.available += f;
flow += f;
r -= f;
if (r <= 0) {
break;
}
}
}
return flow;
}
}