文章目录
2.3 栈的应用——括号匹配与后缀表达式
在解决问题中出现了一个子问题,但是仅凭现有条件无法进行解决,可以将其记下,等待之后出现可以解决它的条件以后再返回来解决。这种问题就可以利用栈的压栈操作来进行记忆,这是栈的FILO特性所衍生出来的。
1、括号匹配问题
题目:编写一个算法,判断一个表达式中的括号是否正确配对,假设表达式中只有小括号,表达式已经存入ecp[]中,表达式中的字符个数为n。
思路:从头遍历表达式数组,当遇见’(‘时,将其压入准备的栈中等候处理,如果遇到’)’,若此时栈空,则不匹配,否则将栈中的’(‘中弹出一个;当遍历完成以后,如果存储’('的栈为空,说明所有的括号都匹配成功了,否则不匹配。图解如下:
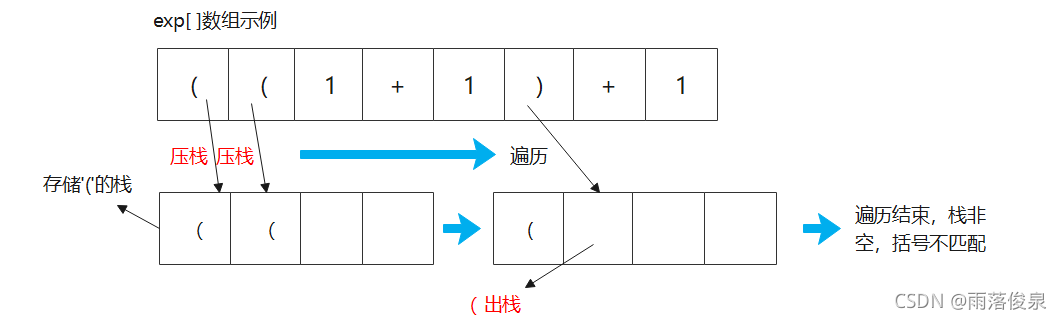
代码实现如下
public class BracketMatching {
//利用栈完成括号匹配
boolean match(char[]exp){
char stack[] = new char[exp.length];
int top=-1;
for (int i=0;i<exp.length;i++){
if (exp[i]=='('){
stack[++top]='(';//遇到'('则入栈
}
if (exp[i]==')'){
if (top==-1){
return false;//栈空说明')'比'('多,不匹配
}else {
--top;//栈不空则将栈中的一个'('弹出
}
}
}
if (top==-1){
return true;//栈空则说明所有括号都被处理掉
}
return false;//否则括号不匹配
}
public static void main(String[] args) {
BracketMatching test = new BracketMatching();
String string = "((1+1)+(2+1)))";
char[] exp=string.toCharArray();
System.out.println(string+"括号匹配: "+test.match(exp));
}
}
运行结果
((1+1)+(2+1)))括号匹配: false
2、前缀、中缀、后缀表达式
算术表达式分为前缀式、中缀式、后缀式。
(1) 前缀表达式(波兰表达式)
1)前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前
2)举例说明: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6
前缀表达式的计算机求值
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果
1?? 例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下
从右至左扫描,将6、5、4、3压入堆栈
遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素),计算出3+4的值,得7,再将7入栈
接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈
最后是-运算符,计算出35-6的值,即29,由此得出最终结果
(2) 中缀表达式
1)中缀表达式就是常见的运算表达式,如(3+4)×5-6
2)中缀表达式的求值是我们人最熟悉的,但是对计算机来说却不好操作,因此,在计算结果时,往往会将中缀表达式转成其它表达式来操作(一般转成后缀表达式.)
(3) 后缀表达式
1)后缀表达式又称逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后
2)中举例说明: (3+4)×5-6 对应的后缀表达式就是3 4 + 5 × 6 –
后缀表达式的计算机求值
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
2?? 例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下
从左至右扫描,将3和4压入堆栈;
遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素),计算出3+4的值,得7,再将7入栈;
将5入栈;
接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
将6入栈;
最后是-运算符,计算出35-6的值,即29,由此得出最终结果
示例代码如下
public class Postfix_Expression_Calculation {
//利用栈对后缀表达式求值
//简化起见,每个数字只有一位,且假设表达式都能正常计算
static int calculate(String expS) {
Stack<Integer> stack = new Stack<>();//存储数字的栈
char[] exp = expS.toCharArray();
for (int i = 0; i < exp.length; i++) {
if (exp[i] >= '0' && exp[i] <= '9') {//遇到数字则压栈
stack.push(exp[i] - '0');
} else if (exp[i] != ' ') {
int num2 = stack.pop();
int num1 = stack.pop();//弹出栈顶的两个元素
int temp = -1;//存储中间结果
switch (exp[i]) {
case '+':
temp = num1 + num2;
break;
case '-':
temp = num1 - num2;
break;
case '×':
temp = num1 * num2;
break;
case '/':
temp = num1 / num2;
break;
}
stack.push(temp);//将中间结果压栈
}
}
return stack.peek();//返回栈顶元素
}
public static void main(String[] args) {
String exp = "1234×++2/";
int result = calculate(exp);
System.out.println("the result of Postfix_Expression:" + exp + "is " + result);
}
}
运算结果如下:
the result of Postfix_Expression:1234×++2/is 7
(4) 中缀表达式转化为后缀表达式
在开发中,我们需要将中缀表达式转化为后缀表达式,算法如下
1?? 初始化两个栈:运算符栈s1和储存中间结果的栈s2;
2?? 从左至右扫描中缀表达式;
3?? 遇到操作数时,将其压s2;
4?? 遇到运算符时,比较其与s1栈顶运算符的优先级:
- 如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
- 否则,若优先级比栈顶运算符的高,也将运算符压入s1;
- 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较;
5?? 遇到括号时:
- 如果是左括号“(”,则直接压入s1
- 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
6?? 重复步骤2至5,直到表达式的最右边
7?? 将s1中剩余的运算符依次弹出并压入s2
8?? 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式
举例说明 将中缀表达式1+((2+3)×4)-5转换为后缀表达式
| 扫描到的元素 | s2(栈底->栈顶) | s1 (栈底->栈顶) | 说明 |
|---|---|---|---|
| 1 | 1 | 空 | 数字,直接入栈 |
| + | 1 | + | s1为空,运算符直接入栈 |
| ( | 1 | + ( | 左括号,直接入栈 |
| ( | 1 | + ( ( | 同上 |
| 2 | 1 2 | + ( ( | 数字 |
| + | 1 2 | + ( ( + | s1栈顶为左括号,运算符直接入栈 |
| 3 | 1 2 3 | + ( ( + | 数字 |
| ) | 1 2 3 + | + ( | 右括号,弹出运算符直至遇到左括号 |
| × | 1 2 3 + | + ( × | s1栈顶为左括号,运算符直接入栈 |
| 4 | 1 2 3 + 4 | + ( × | 数字 |
| ) | 1 2 3 + 4 × | + | 右括号,弹出运算符直至遇到左括号 |
| - | 1 2 3 + 4 × + | - | -与+优先级相同,因此弹出+,再压入- |
| 5 | 1 2 3 + 4 × + 5 | - | 数字 |
| 到达最右端 | 1 2 3 + 4 × + 5 - | 空 | s1中剩余的运算符 |
代码实现:
public class Nifix_to_Postfix {
//输入一个中缀表达式,将其转换为后缀表达式
//简化起见,每个数字只有一位,且假设表达式都能正常计算
static String change(String nifix) {
Stack<Character> s1 = new Stack<>();//存储运算符的栈
Stack<Character> s2 = new Stack<>();//存储中间结果的栈
char[] nifixExp = nifix.toCharArray();//将字符串转化为字符数组
for (int i = 0; i < nifixExp.length; i++) {//从左到右扫描
if (nifixExp[i] >= '0' && nifixExp[i] <= '9') {
s2.push(nifixExp[i]);//遇到数字则压入s2
} else if (nifixExp[i] == '(') {
s1.push(nifixExp[i]);//左括号直接压入s1
} else if (nifixExp[i] == ')') {
while (s1.peek()!='('){
s2.push(s1.pop());
}
s1.pop();//把左括号也弹出
} else {
/**
* 遇到运算符时,比较其与s1栈顶运算符的优先级:
* 1) 如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
* 2) 否则,若优先级比栈顶运算符的高,也将运算符压入s1;
* 3) 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(1)与s1中新的栈顶运算符相比较;
*/
while (true) {
if (s1.empty() || s1.peek() == '('
|| comparePriority(nifixExp[i], s1.peek())) {
s1.push(nifixExp[i]);
break;
} else {
s2.push(s1.pop());
}
}
}
}
//把s1中剩余的运算符一次弹出并压入s2
while(!s1.empty()){
s2.push(s1.pop());
}
//依次弹出s2中的元素并输出,
// 结果的逆序即为中缀表达式对应的后缀表达式
char [] temp=new char[s2.size()];
for (int i = 0; !s2.empty() ; i++) {
temp[i]=s2.pop();
}
String string = "";
for (int i = temp.length-1; i >=0 ; i--) {
string+=temp[i];
}
return string;
}
private static boolean comparePriority(char c1, char c2) {//比较运算符优先级
int priority1 = (c1 == '+' || c1 == '-' ? 1 : 2);
int priority2 = (c2 == '+' || c1 == '-' ? 1 : 2);
if (priority1 - priority2 > 0) {
return true;//c1优先级较高
}
return false;
}
public static void main(String[] args) {
String test = "(1+2+3×4)/3";
System.out.println("\"" +test+"\" after change: \""+change(test)+"\"");
System.out.println("the result of Postfix_Expression: \""+change(test)+"\" is "
+Postfix_Expression_Calculation.calculate(change(test)));
}
}
运行结果如下:
"(1+2+3×4)/3" after change: "12+34×+3/"
the result of Postfix_Expression: "12+34×+3/" is 5
3、综合应用——求布尔表达式的值
西交的软件朋友们,此题仅供思路参考,千万不要复制粘贴
题目:
本题是要计算类似如下的布尔表达式:(T |T)& F &(F|T),其中 T 表示 True,F 表示 False。表 达式可以包含如下运算符:!表示 not(非),&表示 and(与),|表示 or(或),^表示 xor(异 或),并允许使用括号。 为了执行表达式的运算,要考虑运算符的优先级,以上逻辑运算符的优先级由高到低为: not、and、xor、or。括号运算符的优先级高于逻辑运算符。当运算符相同时,遵循左结合。表达 式的计算最终结果只能是 T 或 F。 对输入的表达式的要求如下:
1)一个表达式不超过 100 个字符,字符间可以用任意个空格分开,或者根本没有空格,所以 表达式总的长度也就是字符的个数,它是未知的。
2)要能处理表达式中出现括号不匹配、运算符缺少运算操作数等常见的输入错误。
public class BoolCalculate {
//计算布尔表达式的值
//利用自定义的链栈
static char boolCalculate(String expS) throws Exception {//主函数
LStack<Character> stack = new LStack<>();//存储数字的栈
char[] exp = expS.toCharArray();
for (int i = 0; i < exp.length; i++) {
if (exp[i] == 'T' || exp[i] == 'F') {//遇到T\F则压栈
stack.push(exp[i]);
} else if (exp[i] != ' ') {
char char1 = stack.pop();
char temp;
if (exp[i] == '!') {//取非运算符只需要一个元素
temp = logicCalculate(exp[i], char1, ' ');//存储中间运算结果
} else {
char char2 = stack.pop();//弹出栈顶的第二个元素
temp = logicCalculate(exp[i], char1, char2);//根据运算符进行逻辑运算,存储中间运算结果
}
stack.push(temp);//将中间结果压栈
}
}
return stack.topValue();
}
static char logicCalculate(char operator, char char1, char char2) {//逻辑运算
switch (operator) {
case '!': //非运算
if (char1 == 'T') return 'F';
else return 'T';
case '&': //与运算
if (char1 == 'T' && char2 == 'T') return 'T';
else return 'F';
case '|': //或运算
if (char1 == 'F' && char2 == 'F') return 'F';
else return 'T';
case '^': //异或运算
if ((char1 == 'T' && char2 == 'T') || (char1 == 'F' && char2 == 'F')) return 'F';
else return 'T';
default:
return ' ';
}
}
//中缀转后缀
static String toPostfix(String nifix) throws Exception {
LStack<Character> s1 = new LStack<>();//存储运算符的栈
LStack<Character> s2 = new LStack<>();//存储中间结果的栈
char[] nifixExp = nifix.toCharArray();//将字符串转化为字符数组
for (int i = 0; i < nifix.length(); i++) {
if (nifixExp[i] != 'F' && nifixExp[i] != 'T' && nifixExp[i] != '!'
&& nifixExp[i] != '&' && nifixExp[i] != '|' && nifixExp[i] != '^'
&& nifixExp[i] != ' ' && nifixExp[i] != '(' && nifixExp[i] != ')') {
throw new Exception("输入符号有问题");
}
}
if (!BracketMatching.match(nifixExp)) {
throw new Exception("括号不匹配");
} else {
for (int i = 0; i < nifixExp.length; i++) {//从左到右扫描
if (nifixExp[i] == 'T' || nifixExp[i] == 'F') {
s2.push(nifixExp[i]);//遇到T/F则压入s2
} else if (nifixExp[i] == '(') {
s1.push(nifixExp[i]);//左括号直接压入s1
} else if (nifixExp[i] == ')') {
while (s1.topValue() != '(') {
s2.push(s1.pop());
}
s1.pop();//把左括号也弹出
} else if (nifixExp[i] != ' ') {
/**
* 遇到运算符时,比较其与s1栈顶运算符的优先级:
* 1) 如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
* 2) 否则,若优先级比栈顶运算符的高,也将运算符压入s1;
* 3) 否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(1)与s1中新的栈顶运算符相比较;
*/
while (true) {
if (s1.isEmpty() || s1.topValue() == '('
|| comparePriority(nifixExp[i], s1.topValue())) {
s1.push(nifixExp[i]);
break;
} else {
s2.push(s1.pop());
}
}
}
}
}
//把s1中剩余的运算符一次弹出并压入s2
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
//依次弹出s2中的元素并输出,
// 结果的逆序即为中缀表达式对应的后缀表达式
char[] temp = new char[s2.size()];
for (int i = 0; !s2.isEmpty(); i++) {
temp[i] = s2.pop();
}
String string = "";
for (int i = temp.length - 1; i >= 0; i--) {
string += temp[i];
}
return string;
}
private static boolean comparePriority(char c1, char c2) {//比较运算符优先级
int priority1 = 0, priority2 = 0;
switch (c1) {
case '!':
priority1 = 4;
break;
case '&':
priority1 = 3;
break;
case '^':
priority1 = 2;
break;
case '|':
priority1 = 1;
break;
}
switch (c2) {
case '!':
priority2 = 4;
break;
case '&':
priority2 = 3;
break;
case '^':
priority2 = 2;
break;
case '|':
priority2 = 1;
break;
}
return priority1 - priority2 > 0;//c1优先级较高
}
public static void main(String[] args) throws Exception {
System.out.print("please input your nifix expression: ");
Scanner in = new Scanner(System.in);
String input = in.nextLine();//next()方法不能带空格
char result = boolCalculate(toPostfix(input));
System.out.println("the result of: " + input + " is " + result);
}
}
运行结果如下:
please input your nifix expression: (T |T)& F &(F|T)
the result of: (T |T)& F &(F|T) is F