2.5 队列的应用——基数排序
1、算法介绍
基数排序的关键思想是“多关键字排序”,而其具有两种基本的实现方式
1?? 最高位优先(MSD)
先按最高位排成若干子序列,再对每个子序列依次按高位排序,以扑克牌为例,就是先按照花色排成四个子序列,再对每个花色的13张牌进行排序,最后使整个牌有序。
2?? 最低位优先(LSD)
这种方式不用先分成子序列,每次排序全体关键字都参加。最低位可以优先这样进行,不通过比较,而是通过“分配”和“收集”。同样以扑克牌为例,可以先按照数字将牌分配到1~13的13个桶中,然后从第一个桶开始依次收集;再将收集好的牌按照花色分配到4个桶中,也是从第一个桶开始收集。经过两次“分配”和“收集”操作,最终使牌有序
2、算法流程
以LSD为例,说明基数排序的过程,原始序列为:278 109 63 930 589 184 505 269 8 83
每个关键字的每一位都是由数字组成的,数字的范围是0~9,所以准备10个桶来放关键字,需要注意组成关键字的每一位不一定是数字,也有可能是扑克牌的花色(要准备4个桶),或者是英文字母(不区分大小的话要准备26个桶)。这里的桶,就是一个先进先出的队列。
1?? 进行第一趟分配和收集,按照最后一位
1)分配过程如下(关键字从桶的上面进入)
278的最低位是8,放入桶8中
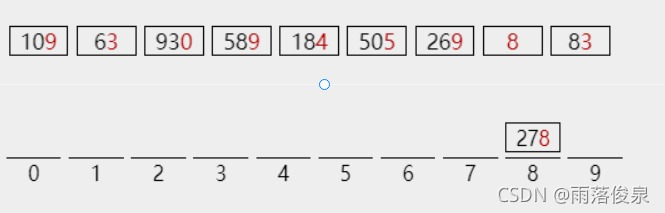
109的最低位是9,放进桶9
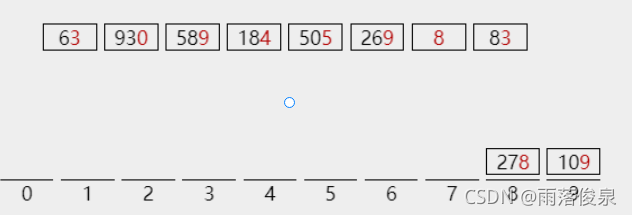
按照以上方法,依次将数字放入桶中,完成第一趟分配

2)收集过程如下,按照0~9的顺序收集,注意关键字从桶的下面收集
桶0:930
桶1:不收集
桶2:不收集
桶3:63、83
…
桶8:278,8
桶9:109,589,269
将每桶收集的关键字依次排开,第一趟收集后的结果为
930 63 83 184 505 278 8 109 589 269
2?? 在第一趟排序结果的基础上,进行第二次分配与收集,按照中间位
1)第二趟分配的结果如下
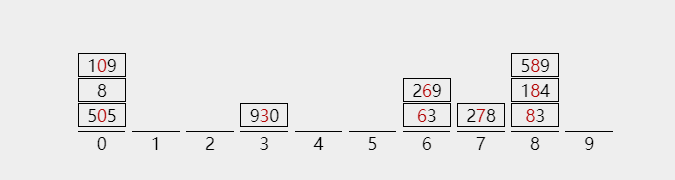
2)第二趟的收集过程如下
桶0:505,8,109
桶1:不收集
桶2:不收集
桶3:930
…
桶8:83,184,589
桶9:不收集
第二趟的收集结果如下:
505 8 109 930 63 269 278 83 184 589
3?? 在第二趟排序结果的基础上,进行第三趟分配与收集,按照最高位
1)第三趟的分配结果如下
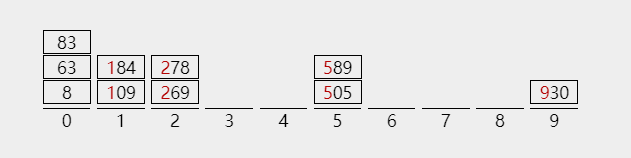
2)进行第三趟收集
桶0:8,63,83
桶1:109,184
桶2:269,178
桶3:不收集
…
桶8:不收集
桶9:930
第三趟的收集结果如下:
8 63 83 109 184 269 278 505 589 930
此时,最高位有序,最高位相同的关键字按照中间位有序,中间位相同的关键字按最低位有序,于是整个序列有序,基数排序结束
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好。MSD的方式与LSD相反,是由高位数为基底开始进行分配,但在分配之后并不马上合并回一个数组中,而是在每个“桶子”中建立“子桶”,将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。
3、算法性能分析
时间复杂度:平均和最坏情况下都是 O ( d ( n + r d ) ) O(d(n+r_{d})) O(d(n+rd?))
空间复杂度: O ( r d ) O(r_{d}) O(rd?)
其中,n为序列中的关键字数,d为关键字的关键字位数,如930,由3位组成,d=3; r d r_{d} rd? 为关键字基的个数,这里的基指的是构成关键字的符号,如关键字为数值时,构成关键字的符号就是0~9这些数字,一共十个,所以 r d = 10 r_{d}=10 rd?=10
??:时间复杂度分析
基数排序每一趟进行分配和收集。分配需要依次对序列中的每个关键字进行,即需要顺序扫描整个序列,所以有n这一项;收集需要依次对每个桶进行,而桶的数量取决于关键字的取值范围,如放数字的桶有10个,放字母的桶有26个,刚好是 r d r_{d} rd? ,所以有 r d r_{d} rd? 这一项,于是进行一趟分配和收集则需要花费 n + r d n+r_{d} n+rd? 。整个排序需要进行的趟数即为关键字的关键字位数,即为d。所以基数排序的时间复杂度即为 O ( d ( n + r d ) ) O(d(n+r_{d})) O(d(n+rd?))
4、举例说明
利用队列实现对某一个数据序列的排序(采用基数排序),其中对数据序列的数据(第 1 和第 2 条进行说明)和队列的存储方式(第 3 条进行说明)有如下的要求:
1)当数据序列是整数类型的数据的时候,数据序列中每个数据的位数不要求等宽,比如: 1、21、12、322、44、123、2312、765、56
2)当数据序列是字符串类型的数据的时候,数据序列中每个字符串都是等宽的,比如: “abc”,“bde”,“fad”,“abd”,“bef”,“fdd”,“abe”
3)要求重新构建队列的存储表示方法:使其能够将 n 个队列顺序映射到一个数组 listArray 中, 每个队列都表示成内存中的一个循环队列【这一项是可选项】
思路:对于数字和等长字符串,可采用最低位优先法排序;对于要求3,即是要用一个存储数组存多个队列的值,这时候可以利用指针数组front[n]和rear[n]进行求解,注意数组下标的变化(这一问我参考了大佬的答案,就不放出来了)
public class RadixSort {
public static void LSD(int[] num) {
//对数字采用最低位优先法排序
MyQueue queue = new MyQueue(10, num.length);//分配10个队列
int digits = getNumDigits(num);
int mode = 1;
while (digits != 0) {
for (int i = 0; i < num.length; i++) {
queue.enqueue((num[i] / mode) % 10, num[i]);
//按桶分配,(num[i]/mode)%10表示取的位数
}
int k = 0;
for (int j = 0; j < 10; j++) {
while (!queue.isEmpty(j)) {
num[k] = (int) queue.dequeue(j);
k++;
}
}//出队
digits--;//位上移
mode = mode * 10;
}
}
public static void LSD(String[] str) {
//对字符串采取最低位优先法
//对数字采用最低位优先法排序
MyQueue queue = new MyQueue(27, str.length);//分配27个队列
//27个桶,其中第27个桶用来存储除字母以外的其他字符,不区分大小写
int digits = str[0].length();//等长字符的长度
int mode = 1;
while (digits != 0) {
for (int i = 0; i < str.length; i++) {
int index;//桶的下标
if (str[i].charAt(digits - 1) >= 'A' && str[i].charAt(digits - 1) <= 'Z') {
index = str[i].charAt(digits - 1) - 'A';
} else if (str[i].charAt(digits - 1) >= 'a' && str[i].charAt(digits - 1) <= 'z') {
index = str[i].charAt(digits - 1) - 'a';
} else {
index = 26;
}//不区分大小写
queue.enqueue(index, str[i]);
//按桶分配
}
int k = 0;
for (int j = 0; j < 27; j++) {
while (!queue.isEmpty(j)) {
str[k] = (String) queue.dequeue(j);
k++;
}
}//出队
digits--;//位上移
}
}
static int getNumDigits(int[] num) {//获得最大的数的位数
int max = num[0];//最大的数
int digits = 0;//位数
for (int i = 0; i < num.length; i++) {
if (num[i] > max) max = num[i];
}
while (max / 10 != 0) {
digits++;
max = max / 10;
}
if (max % 10 != 0) {
digits++;
}
return digits;
}
public static void main(String[] args) {
int[] num = {12, 32, 2, 231, 14, 23};
System.out.println("before sorting: " + Arrays.toString(num));
LSD(num);
System.out.println("after sorting: " + Arrays.toString(num));
String[] strings = {"abc", "bde", "fad", "abd", "bef", "fdd ", "abe" };
System.out.println("before sorting: " + Arrays.toString(strings));
LSD(strings);
System.out.println("after sorting: " + Arrays.toString(strings));
}
}
运行结果如下
before sorting: [12, 32, 2, 231, 14, 23]
after sorting: [2, 12, 14, 23, 32, 231]
before sorting: [abc, bde, fad, abd, bef, fdd , abe]
after sorting: [abc, abd, abe, bde, bef, fad, fdd ]