[数据结构与算法]树与二叉树的应用?

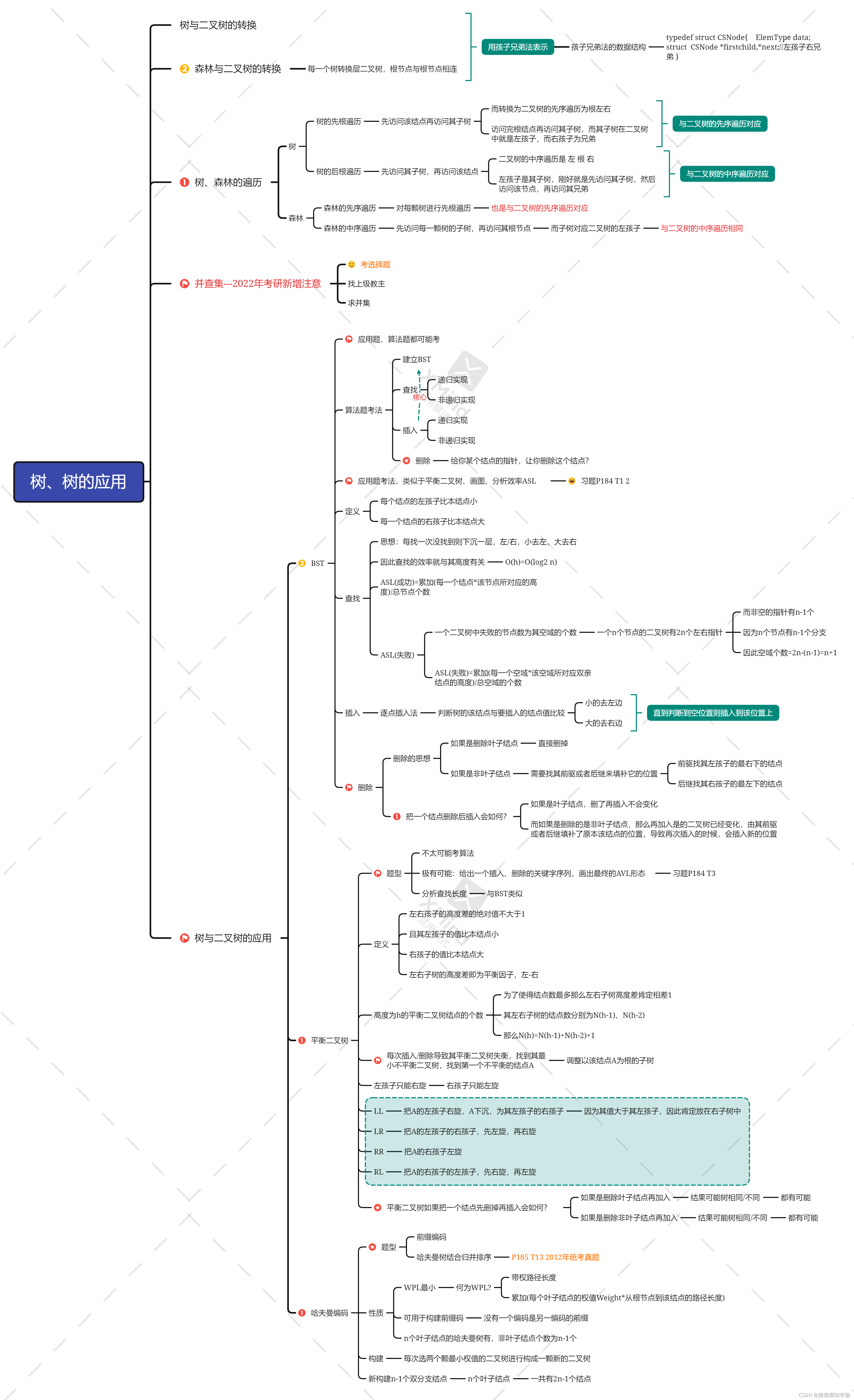
总体框架

习题难题总结归纳

树、森林

P167 T4

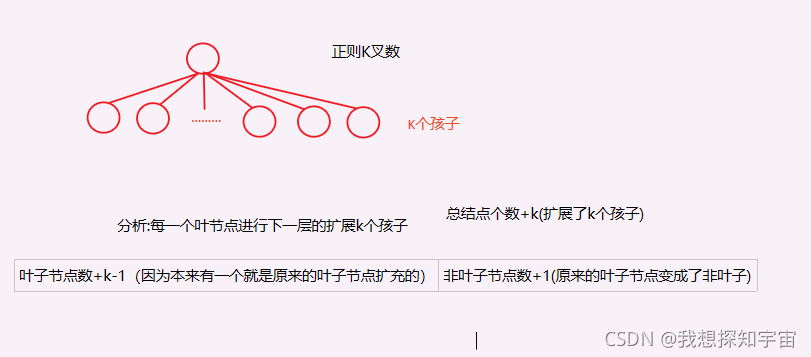
因此每次加入非叶子节点就会使得叶子数新增(k-1)个
因此m个非叶子节点 就会有 1+(k-1)m个叶子结点，而加一是非空至少有一个根结点
①结点数最多的时候是每一个结点都向外扩展k个孩子，那么就是满k叉树，总数为=1+k+k²+k³+…k^h-1=(k^h-1)/(k-1)
②最少的情况就是每一层只有一个结点向外扩展k个孩子，则其他结点都是叶子结点，那么结点个数就为=k(h-1)+1

树与二叉树的应用??

1、P181 T6

法一:直接一个个画图
法二:用二叉排序树 中大于左 中小于右的特性
A中 95 22，所以22在95的左边，后面的序列都必须小于95
22 91，91在22的右边，所以后面序列必须 大于22 小于91
24 ，24在91的左边，因此后面的序列必须 小于24
到这里已经完了，94已经出错大于24了
A

P182 T9

这题2013与2019年真题应该放在一起讨论
一个是二叉排序树的删除再插入
一个是平衡二叉树的插入再删除

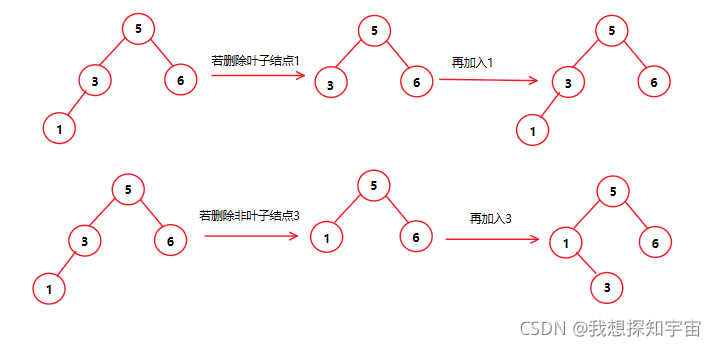
在二叉排序树中删除再插入会有两种情况：
一种是：要删除的是叶子结点，那么直接删除，再插入的时候还会是同一个位置，因为二叉树的形态都没有变化
第二种是：删除的是非叶子结点，那么该二叉树的形态在删除结点之后必定会改变，因为需要用要删除的非叶子结点的前驱或者后继来填补该结点的位置，而一旦树的形态改变了，那么再插入原来删除的结点，必定会插入新的位置。
因此 II 、III是对的 答案选C

P182 T9

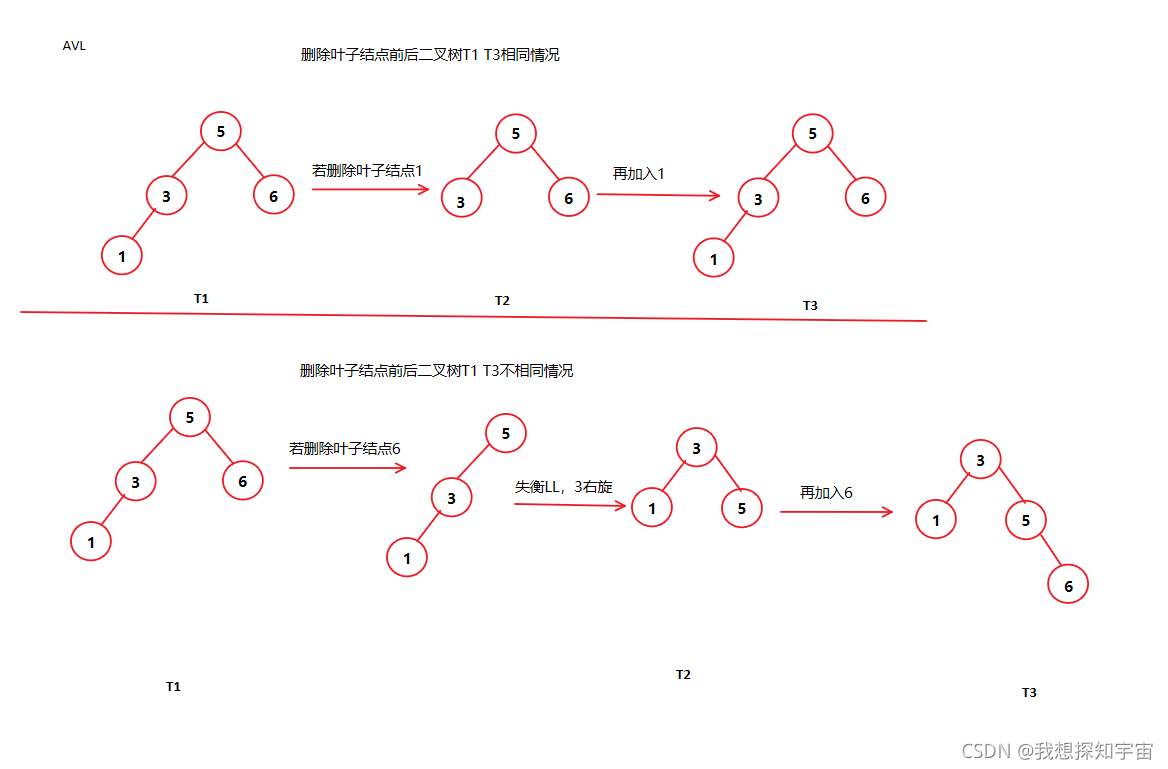
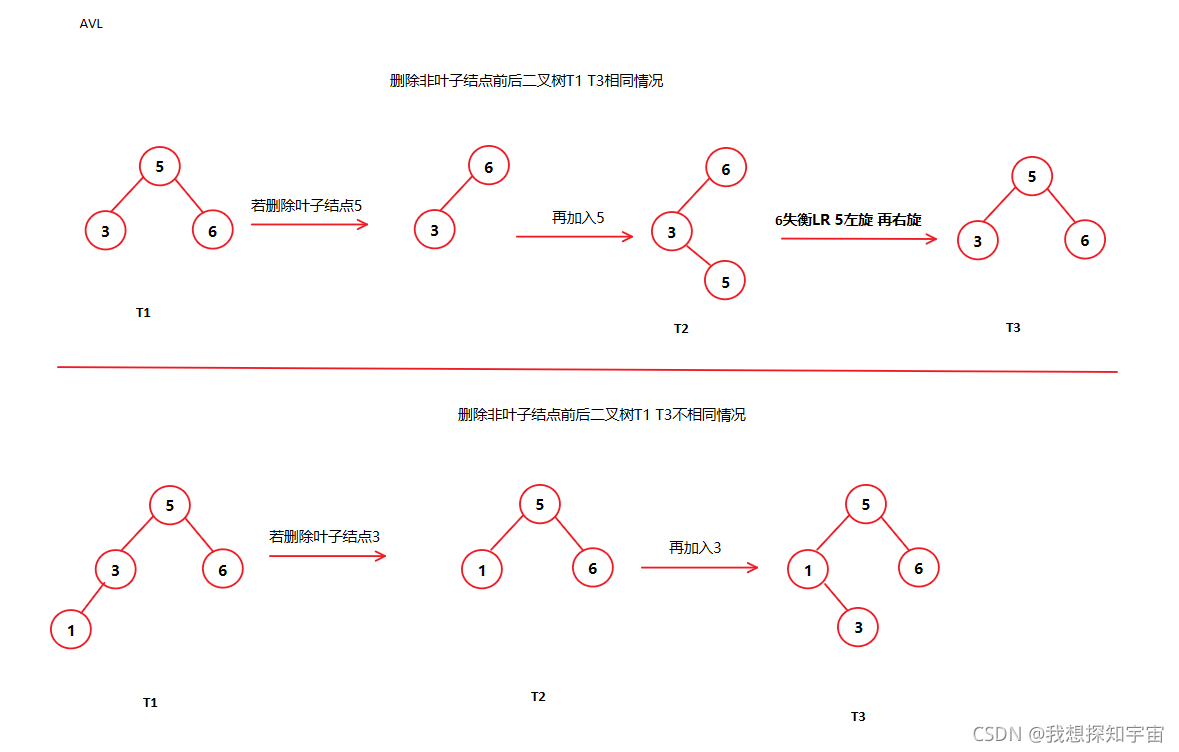
①平衡二叉树删除叶子结点后可能会导致失衡，所以进行了调整树，导致树的形态发生了改变，再插入后，就会放到新的位置上

②平衡二叉树删除非叶子结点同样有可能会树的形态发生变化再插入后到新的位置，也有可能过程中形态发生了变化，但是再插入后又调整回原来的形态

P183 T17、18、19

做题思想很简单：直接画图就完了，非叶子结点平衡因此均为1，左减右必须为1

做题思想很简单：直接画图就完了，画完直接数平衡因此为0的非叶子结点(分支结点)

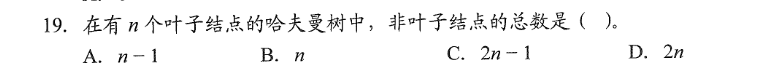
这题就是概念题，拿出来主要是怎么证明非叶子结点的总数为n-1,在哈夫曼树中，每个非叶子结点都必须是度为2的结点，即为有两个孩子
那么一个非空的二叉树中拿一个叶子结点向外扩展2个孩子，非叶子结点数+1，叶子结点数是+1，不是加2，因为扩展需要消耗一个叶子结点。
而扩展了m次有m个非叶子结点，而每扩展一次2个叶子结点孩子需要消化一个叶子结点，所以扩展了m次，叶子结点个数=(2-1)*m+1
加一是因为，扩展的时候必须要有叶子结点，即没有扩展的时候，叶子结点个数为1。
那么就能得出叶子结点的个数=m+1，在这题中m+1=n，所以非叶子结点为m=n-1
A

这题就刚好是上一题我给出的证明的过程的结果，由上一题的推论得出，叶子结点个数=(m-1)*非叶子结点个数+1
通过移项可得：非叶子结点个数=?(叶子结点个数n-1)/(m-1)?

这题呢！与平常的平衡二叉树不一样的地方是，这题的形态是，中比左小，中比右大，所以中序遍历就能得出降序的序列
A平衡二叉树未必根节点的度必须为2，因为可以高度差为1
B未必，因为非叶子结点是小于左孩子的，一旦右孩子没有，那么在该题中就有可能是最小元素的结点
C未必，可能通过旋转上移元素，变成了非叶子结点
D因为该题的左孩子比 本结点元素的值大，如果该结点时最大元素，那么一定没有左子树

综合题BST、AVL、Huffman

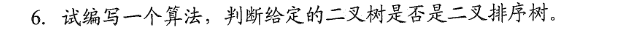
typedef struct BTnode{
	int  data;
	struct BTnode *lchild;//左孩子
	struct BTnode *rchild;//右孩子 
	int weight; 
}BTnode,*BiTree;
int IsBinSortTree(BiTree T){
	int bl,br;
	if(!T)
		return 1;//空默认为真
	if(T->lchild&&T->rchild){//左右孩子都存在 
		if(T->lchild->data>=T->data||T->data>=T->rchild->data)//不符合二叉排序树
			return 0;
		else{
			bl=IsBinSortTree(T->lchild);//查左子树
			br=IsBinSortTree(T->rchild);//查右子树
			return br&&bl; 
		}
	}
	else{//左右子树有个为空
		
		if(T->lchild){//左子树 
			if(T->lchild->data>=T->data)//左子树值大于本结点，不符合
				return 0;
			else
				return IsBinSortTree(T->lchild);//查左子树
		}
		else if(T->rchild){//右子树 
			if(T->rchild->data<=T->data)//右子树值小于于本结点，不符合
				return 0;
			else
				return IsBinSortTree(T->rchild);//查左子树
		}
		else
			return 1;
		
	}
	return 1;
} 

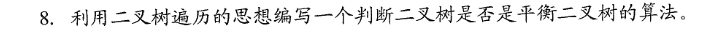
思想：左右子树高度差小于1，且遵循二叉排序树原理,先判断是否是二叉排序树，在判断是否是平衡二叉树

void IsBalanceTree(BiTree T,int &balance,int &h){
	int hl,hr;//高度差 
	int bl,br;//用于判断是否遵循平衡
	if(!T){
		h=0;
		balance=1;//空树平衡 
	} 
	else if(!T->lchild&&!T->rchild){//左右子树都为空 
		h=1;
		balance=1; 
	}
	else{//有左子树或者右子树 
		IsBalanceTree(T->lchild,bl,hl);//递归左子树
		IsBalanceTree(T->rchild,br,hr);//递归左子树
		h=(hl>hr?hl:hr)+1;
		if(abs(hl-hr)<2)
			balance=bl&&br;
		else
			balance=0;
	}
}
int IsBinSortTree(BiTree T){
	int bl,br;
	if(!T)
		return 1;//空默认为真
	if(T->lchild&&T->rchild){//左右孩子都存在 
		if(T->lchild->data>=T->data||T->data>=T->rchild->data)//不符合二叉排序树
			return 0;
		else{
			bl=IsBinSortTree(T->lchild);//查左子树
			br=IsBinSortTree(T->rchild);//查右子树
			return br&&bl; 
		}
	}
	else{//左右子树有个为空
		
		if(T->lchild){//左子树 
			if(T->lchild->data>=T->data)//左子树值大于本结点，不符合
				return 0;
			else
				return IsBinSortTree(T->lchild);//查左子树
		}
		else if(T->rchild){//右子树 
			if(T->rchild->data<=T->data)//右子树值小于于本结点，不符合
				return 0;
			else
				return IsBinSortTree(T->rchild);//查左子树
		}
		else
			return 1;
		
	}
	return 1;
}
void IsBalanceSortTree(BiTree T,int &balance,int &h){
	if(IsBinSortTree(T))
		IsBalanceTree(T,balance,h);
	else
		balance=0;
}

分析2012年统考真题

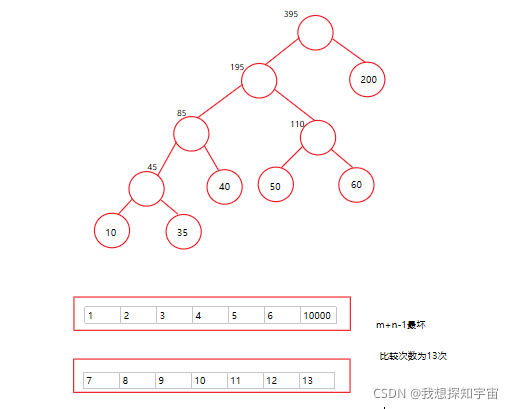
先分析：题目要求归并且要使得最坏的情况下的比较的总次数达到最小，所以采用了Huffman+二路归并的思想

1)因为两个序列的比较次数最坏是m+n-1次，而每次合并如果随机合并会 长合短 ，长合长 ，短和短三种情况，长合短、长合长都有可能使得比较的总次数增多，而全用短合短保证了把大的留在后面使得比较次数少了
因此最坏的比较总次数=哈夫曼树的WPL-合并的次数，每次合并最坏的情况都会有最后一个元素没有参与比较
所以最坏的比较总次数=4x(10+35)+(40+50+60)x3+110x2+200x1-5=825

1）哈夫曼树，树结构保存上述具有前缀特性的不等长编码
2）因为每个字符的编码都不是其他字符编码的前缀，所以通过字符串的子串与每个字符的编码进行比较，通过KMP字符串比较算法即可获得最长的匹配公共子序列，而得到的这个子序列的0/1串对应的字符就是对应子串字符，通过不断得比较，便可从获得从起点到终点的0/1子串对应的字符串了。
3）通过把字符集中的每一个不等长编码，都与其他不等长的编码进行字符串KMP匹配算法比较，看看是否能匹配成功，如果匹配成功则说明字符集中有不等长的编码是其他不等长编码的子集，说明该字符集不具有前缀特性，而若都匹配失败，说明这个字符集中，没有一个字符编码是其他字符编码的子集，则这个字符集的不等长编码就具有前缀特性