[数据结构与算法]leetCode第509题——斐波那契数

一、题目

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0
F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给你 n ，请计算 F(n) 。提示：0 <= n <= 30

示例 1：
输入：2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：
输入：3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：
输入：4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

二、思路及图解（动态规划方式实现）

1、思路

• 斐波那契数的边界条件是 F(0)=0 和 F(1)=1。当 n>1 时，每一项的和都等于前两项的和，因此有如下递推关系：
• F(n)=F(n?1)+F(n?2)
• 由于斐波那契数存在递推关系，因此可以使用动态规划求解。

2、图解

• 初始化p=0，q=0，r=1；第一次遍历，当i=2时，把q的值0赋值给p，再把r的值1赋值给q，最后把p的值和q的值相加赋值给r，如下图：
  
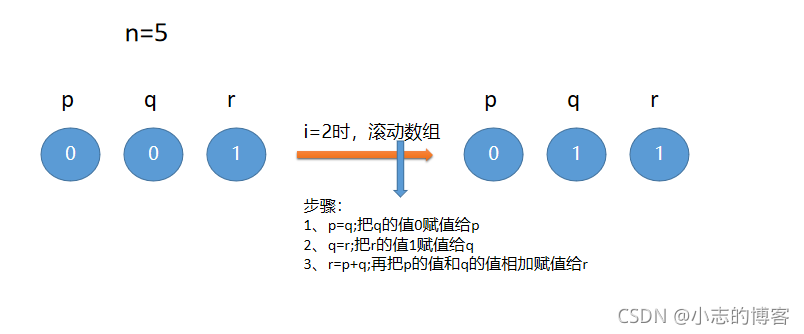
• 在第一次遍历的结果上，第2次遍历，当i=3时，把q的值1赋值给p，再把r的值1赋值给q，最后把p的值和q的值相加赋值给r，如下图：
  
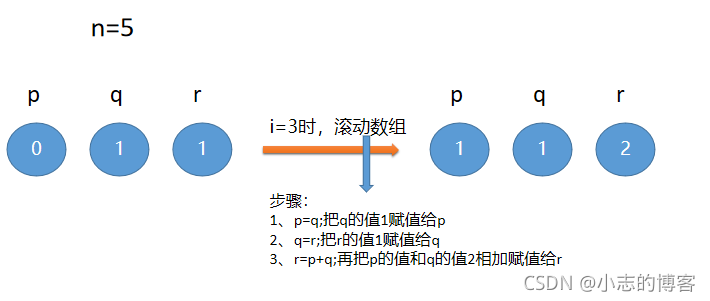
• 在第二次遍历的结果上，第3次遍历，当i=4时，把q的值1赋值给p，再把r的值2赋值给q，最后把p的值和q的值相加赋值给r，如下图：
  
• 在第三次遍历的结果上，第4次遍历，当i=5时，把q的值2赋值给p，再把r的值3赋值给q，最后把p的值和q的值相加赋值给r，并返回r的值，如下图：
  

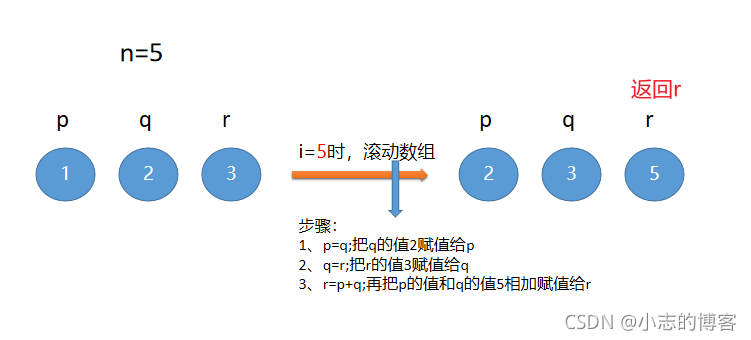
三、题目代码解析（动态规划方式实现）

1、代码

public class Test {
    public static void main(String[] args) {
        //int a=fib(5);
        int a=fibs(5);
        System.out.println("斐波那契数为【"+a+"】");
    }
    /**
     * 动态规划方式实现
     */
    public static int fib(int n){
        if (n < 2) {
            return n;
        }

        int p = 0, q = 0, r = 1;
        for (int i = 2; i <= n; ++i) {
            p = q;
            q = r;
            r = p + q;
        }
        return r;
    }
}

2、结果如下图：

3、复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(1)

四、思路（通项公式实现）

五、题目代码解析（通项公式实现）

1、通过公式直接求解第 n 项，代码如下：

public class Test {
    public static void main(String[] args) {
        int a=fibs(5);
        System.out.println("斐波那契数为【"+a+"】");
    }
     /**
     * 通项公式方式实现
     */
    public static int fibs(int n) {
        double sqrt5 = Math.sqrt(5);
        double fibN = Math.pow((1 + sqrt5) / 2, n) - Math.pow((1 - sqrt5) / 2, n);
        return (int) Math.round(fibN / sqrt5);
    }

}

2、结果如下图：