树状数组：花式前缀和

我们知道前缀和是十分高效的，可以以O(1)的速度求出任意一段连续区间的和，但缺点是数组不可修改，但树状数组的出现提供了转机

一、位运算：lowbit()

树状数组是基于位运算的，所以在介绍树状数组前要介绍lowbit()

lowbit(x)：x在二进制下最低位的1所对应的十进制下的数值

乍一看有些拗口，举些例子：

lowbit(9) = lowbit(1001) = 1
lowbit(40) = lowbit(101000) = 8
lowbit(58) = lowbit(111010) = 2
lowbit(96) = lowbit(1100000) = 32

那么怎么通过推导得到lowbit()的呢？这里不展开讲了，在下篇的算法合集中会来细讲位运算，这里之间给出lowbit()的方法体

lowbit(x) = x & -x

二、树状数组介绍

先放上一张总览的图片
其中c[]表示树状数组，最下方的数组为原始数组。可以看到树状数组的每个index包括了哪些值
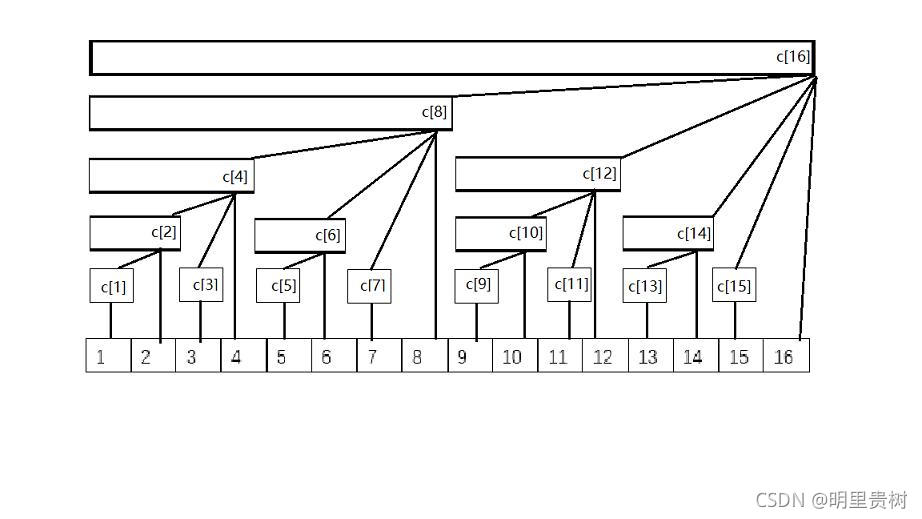
树状数组图示
若要展开来讲树状数组以及他和lowbit()的关系，我们将每个数转换成二进制标在该数旁边。
读者可以先试着去寻找其规律
二进制展开的树状数组
1、查询
树状数组用来记录前缀和，但显然c[x]记录的值并非是c[1] ~ c[x]
这里我们查询时采用这种方法：

sum[1,10] = sum[1,8] + sum[9,10] = c[8] + c[10]
sum[1,15] = sum[1,8] + sum[9,12] + sum[13,14] + sum[15] = c[8] + c[12] + c[14] + c[15]

在图中的二进制中，结合lowbit()寻找关系
发现sum[1,x] = c[x] + c[x - lowbit(x)] + c[x - lowbit(x) - lowbit(x - lowbit(x))] + …

public int query(int x) {
	int ans = 0;
	for (; x > 0; x -= lowbit(x))
		ans += c[x];
	return ans;
}

所以若求sum[x,y]，也就是求query[y] - query[x - 1]
2、更新
树状数组可以维护前缀和，也就是支持更新。
我们对原始数组的每一次更新，在c[]中都要更新该位置及其父亲所在位置，否则查询便会出错

c[x]的父亲是c[x + lowbit(x)]

如果我们暴力的将原始数组的a[x]修改成target，会发现c[x]的父结点不知道怎么改，毕竟该父结点是多个数的和，所以我们采用增量修改

增量修改：先计算出target和origin的差值a，利用a更新c[]

另外要强调的是，c[]的下标是从1开始的，origin的下标不一定从1开始

public void update(int x, int target) {
	int a = target - origin[x]; // origin是原始数组
	origin[x++] = target; // c的下标从1开始，而origin从0开始
	for (; x >= origin.length; x += lowbit(x))
		c[x] += a;
}

3、创建
我们可以利用update()来创建树状数组。

public void build(int[] nums) {
	this.len = nums.length;
	// 我们需要自己保存origin来实现update()，origin的下标可以从0或1开始
	this.origin = new int[len]; 
	c = new int[len + 1]; // 树状数组下标从1开始
	for (int i = 1; i <= len; i++)
		update(i, nums[i - 1]);
}

三、离散化

提到树状数组，就不得不提离散化
下考虑下面的场景

你是一家公司的仓库管理员，你们公司有四个仓库，序号分别为：1，10，100，1000
每个仓库中都有一些货物，每天这些货物的数量都会因买入卖出发生变动
老板希望每次都能以最快的速度计算出任意两个相邻个仓库一共有多少货物

我们知道树状数组可以来帮助完成这个任务，但树状数组的长度应该是多少？1001吗？
答案是5，因为我们将1，10，100，1000离散化成1，2，3，4，节约空间。
所以只需要一个map记录映射关系即可

-2147483648，-64382.1293，-398749174，0，1e9 + 7，2147482647

哪怕有小数，哪怕他们的差值再大，都可以通过离散化来压缩至1，2，3…
思路也十分清晰

利用HashSet记录所有数值，防止重复的值映射成不同的value
将set转换成list进行排序
利用HashMap建立映射关系

Set<Integer> set = new HashSet<>(); // Long，String，Double都可以
for (int x : num)
    set.add(x);
List<Integer> l = new ArrayList<>(set);
Collections.sort(l);
HashMap<Integer, Integer> map = new HashMap<>();
int count = 1;
for (int x : l)
    map.put(x, count++);

每次查询或更新时通过map来找到映射关系即可

四、实战题目：LeetCode 307 区域和检索 - 数组可修改

这题就是为树状数组量身定做的题目
树状数组必须要注意的是，c从1开始而origin下标不一定从1开始，下面的代码中origin从0开始

int[] c;
int[] origin;
int len;
public NumArray(int[] nums) {
    this.len = nums.length;
    c = new int[len + 1];
    origin = new int[len];
    for (int i = 0; i < len; i++)
        update(i, nums[i]);
}
    
public void update(int index, int val) {
    int a = val - origin[index];
    origin[index++] = val;
    for (; index <= len; index += lowbit(index))
        c[index] += a;
}
    
public int sumRange(int left, int right) {
    return query(right + 1) - query(left);
}

private int query(int x) {
    int ans = 0;
    for (; x > 0; x -= lowbit(x)) ans += c[x];
    return ans;
}

private int lowbit(int x) {
    return x & -x;
}

五、树状数组变式：支持区间查找的HashMap

1、LeetCode 327 区间和个数
答案是去寻找，对于任意的i > j，使得lower <= sum[j, i] <= upper有多少组
那么便想到前缀和，对于任意的i > j，使得lower <= s[i] - s[j - 1] <= upper
换个说法，对于任意的i，寻找一个小于i的j，使得s[i] - upper <= s[j] <= s[i] - lower

对于前缀和，直接使用前缀和数组s[]即可，因为这里的原始数组的数据是不变的
用树状数组c[]，利用query(r) - query(l - 1)来帮我们定位到介于(s[i] - upper, s[i] - lower)之间的s[j]有多少个，树状数组记录的是数量。

写法类似于LeetCode 1 两数之和，取s[i]，利用树状数组寻找满足条件的s[j]，然后将s[i]放入树状数组。
这里的树状数组充当了支持区间查找的HashMap，此hashmap记录的是某个值的数量，query(l, r)相当于hashmap.get(l) + hashmap.get(l + 1) + ... + hashmap.get(r)，update(x)相当于hashmap.put(x, 1)

for (long x : s) { // bit是树状数组
    ans += bit.query(map.get(x - upper), map.get(x - lower)); // map为离散化的映射
    bit.update(map.get(x)); // 将s[i]放入树状数组
}

1）先求出前缀和数组并完成离散化
由于前缀和数组中数字之间差值较大，所以利用map进行离散化

int len = nums.length;
long[] s = new long[len + 1];
for (int i = 1; i <= len; i++)
    s[i] = s[i - 1] + nums[i - 1];
        
// 离散化
Set<Long> set = new HashSet<>();
for (long x : s) {
    set.add(x);
    // s[i] - upper <= s[j] <= s[i] - lower
    // 树状数组需要目标区间的首尾来进行query(r) - query(l - 1)
    set.add(x - lower);
    set.add(x - upper);
}
List<Long> list = new ArrayList<>(set);
Collections.sort(list);
HashMap<Long, Integer> map = new HashMap<>();
int count = 1;
for (long x : list)
    map.put(x, count++);

2）实现树状数组(BIT)

与传统的树状数组不同，这里的BIT的update()并不是update(int x, int val)
由于树状数组记录的是数量，所以只需单点更新，使数量+1即可

public void update(int x) {
    for (; x < len; x += lowbit(x))
        c[x]++;
}

BIT类

private class BIT {
    int[] c;
    int len;
    BIT(int len) {
        c = new int[len];
        this.len = len;
    }

    public int query(int l, int r) {
        return query(r) - query(l - 1);
    }

    public void update(int x) {
        for (; x < len; x += lowbit(x))
            c[x]++;
    }

    private int query(int x) {
        int ans = 0;
        for (; x > 0; x -= lowbit(x)) ans += c[x];
        return ans;
    }

    private int lowbit(int x) {
        return x & -x;
    }
}

3）主方法体
在BIT和离散化完成后，需要做的就是寻找s[j] + 放入s[i]

BIT bit = new BIT(l.size() + 1);
int ans = 0;
for (long x : s) {
    ans += bit.query(map.get(x - upper), map.get(x - lower));
    bit.update(map.get(x));
}
return ans;