[数据结构与算法]《遗传算法原理及应用》笔记—遗传算法的高级实现技术

四、遗传算法的高级实现技术

笔者最近在学习遗传算法，希望可以通过笔记对遗传算法做一个简要的介绍与记录。也欢迎小伙伴们一起学习交流。

4.1 倒位算子

所谓倒位操作就是指颠倒个体编码串中随机指定的二个基因座之间的基因排列顺序，从而形成一个新的染色体。

1. 在个体编码串中随机指定两个基因座之后的位置为倒位点
2. 以倒位概率$p_i$颠倒这二个倒位点之间的基因排列顺序。

4.2 二倍体与显性操作因子

二倍体的定义生物已经学过了，用遗传算法进行解释：
二倍体提供了一种机制，它记忆以前有用的基因以及基因的组合；而显性提供了一种算子，它保护所记忆的基因免受有害选择运算所破坏。

4.2.1 二倍体结构的生物基础

4.2.2 二倍体结构在遗传算法中的实现方案

Hollstien 提出了二倍体与显性操作的双基因座显性映射方法。在该方法中，每个二进制基因用两个基因来描述，一个称为函数基因，一个称为修饰基因，取通常含义的0或1值；另一个称为修饰基因，取值为M或m，其中M表示显性基因，m表示隐性基因。对函数基因取值为0的基因，当两个同源染色体中至少有一个修饰基因是M时，则该基因呈显性，否则该基因呈隐性。这种映射关系入图所示。

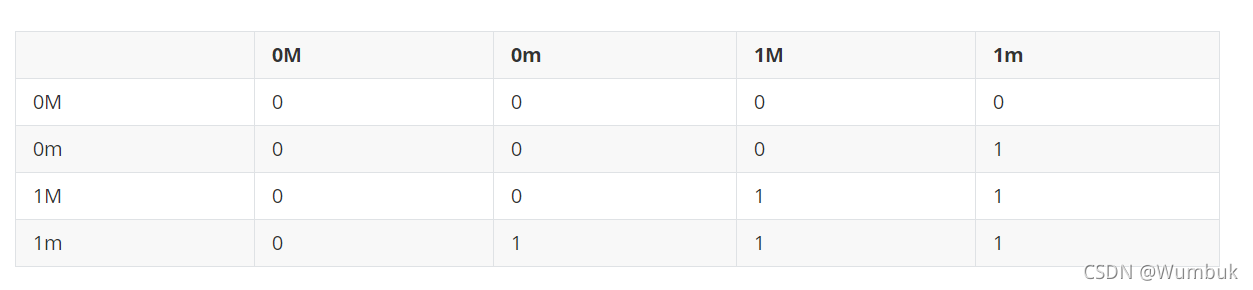
随后，Hollstien将这种映射关系简化为单基因座显性映射方法。Holland对这种单基因座的显性映射描述方法进行了改进，使其表述更加清楚，在这个单基因座显性映射方法中，描述基因字符集为$0,1,1_0$，其中$1_0$为隐性的1，1为显性的1，其映射关系如下所示：

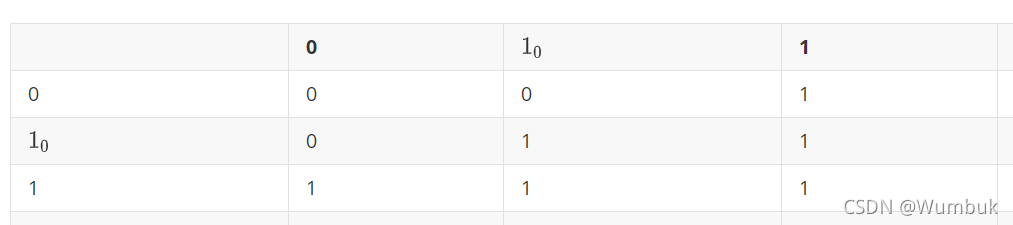
4.3 变长度染色体遗传算法

Goldberg等提出的Messy GA（MGA）是一种典型的变长度染色体遗传算法。现将其基本思想介绍如下：

4.3.1 变长度染色体遗传算法的编码与解码

将常规遗传算法的染色体编码串中各基因座位置及相应基因值组成一个二元组，把这个二元组按一定顺序排列起来，就组成了变长度染色体的一种通用的编码方式。一般可以表示为：
$$X^m:(i_1,v_1)(i_2,v_2)...(i_k,v_k)...(i_n,v_n)$$
上述变长度染色体的描述形式中，$i_k$是所描述的基因在原常规染色体中的基因座编号，$v_k$为对应的基因值。

• 过剩指定
• 缺省指定

4.3.2 切断算子与拼接算子

1. 切断算子
   切断算子以某一预先指定的概率，在变长度染色体中随机选择一个基因座，在该处将个体的基因型切断，使之称为二个个体的基因型。
2. 拼接算子
   拼接算子以某一预先指定的概率，将二个个体的基因型连接在一起，使它们合并为一个个体的基因型。

4.4 小生境遗传算法

4.4.1 小生境与遗传算法

1. 基于预选择的小生境实现方法
   仅当新产生的子代个体的适应度超过其父代个体的适应度时，其产生出的子代个体才能替换其父代个体而遗传到下一代群体中
2. 基于排挤的小生境实现方法
   设置一排挤因子CF，由群体中随机选取的1/CF个个体组成排挤成员，然后依据新产生的个体与排挤成员的相似性来排挤掉一些与排挤成员相类似的个体。
3. 基于共享函数的小生境实现方法
   通过反应个体之间相似程度的共享函数来调整群体中各个个体的适应度，从而在这以后的群体进化过程中，算法可以依据这个调整后的的新的适应度来进行选择运算，以维护群体的多样性。 ? 共享函数是表示群体中两个个体之间密切关系程度的一个函数，可记为$S(d_{ij})$,其中$d_{ij}$ 表示个体i和个体j之间的某种关系。在这里表示为个体基因型或表现型的相似度上。二者呈正相关。
   共享度是某个个体在群体中共享程度的一种度量，它定义为该个体与群体内其它各个个体之间的共享函数值之和，用$S_i$表示：
   $$S_i=\sum _{j=1}^{M}S(d_{ij})(i=1,2,...M)$$
   在计算了群体中各个个体的共享度之后，依据下式来调整各个个体的适应度：
   $$F_i^{\prime }(X)=F_i(X)/S_i(i=1,2,...M)$$

4.5 混合遗传算法

4.5.1 混合遗传算法的思想

因为梯度法、爬山法、模拟退火法、列表寻优法等一些优化算法却具有很强的局部搜索能力，而另外一些含有问题与相关知识的启发式算法的运行效率也比较高，所以我们尽量将二者融合。

由上图可以看出，我们混合遗传算法特点有

1. 引入了局部搜索过程
2. 增加了编码变换操作过程

4.5.2 混合遗传算法的基本构成原则

1. 尽量采用原有算法的编码
2. 利用原有算法的优点
3. 改进遗传算子

4.5.3模拟退火算法

模拟退火算法就是基于金属退火的机理而建立起的一种全局最优化方法，它能够以随机搜索技术从概率的意义上找出目标函数的全局最小点。模拟退火算法的够成要素如下：

1. 搜索空间$\Omega$
2. 能量函数E(x)
3. 状态转移规则P
4. 冷却进度表T(t)

4.5.4 遗传模拟退火算法

即，在遗传算法的运行过程中也应该允许产生个别适应度不高的个体。
遗传算法适合于全局搜索，而退火算法适合于局部搜索。

1. 遗传模拟退火算法
2. 并行组合模拟退火算法

4.5.5 混合遗传算法在求解背包问题中的应用

总结

这就是遗传算法的高级实现技术的大概总结了~