[数据结构与算法]逻辑回归模型——公式推导与python代码实现

1.前言

??逻辑回归模型虽然名字是回归，但是实际上是一种二类(0或1)分类模型。在本文中，0代表负类，1代表正类。逻辑模型的输入为样本的特征向量$\mathbf{x}$，输出为$P(y=1|\mathbf{x})$和$P(y=0|\mathbf{x})$，即在输入特征向量为$\mathbf{x}$条件下，样本标签属于某一类的概率。因为本文讨论的只是二类分类模型，所以有$P(y=1|\mathbf{x})+P(y=0|\mathbf{x})=1$。在实际使用过程中，一般是需要指定一个阈值，比如0.5，如果逻辑回归模型的输出$P(y=1|\mathbf{x})\ge 0.5$，则认为此样本为正类，如果$P(y=1|\mathbf{x})<0.5$,则认为样本为负类。当然阈值是根据实际需求设置的，如果对正类的要求比较严格，则可以将阈值设的高一点，比如0.7。

2.逻辑回归模型

??首先我们来说一下线性回归，我们知道线性回归是用一个一元方程来拟合输入$\mathbf{x}$与输出$y$之间的关系：
$$y=\mathbf{w}?\mathbf{x}+b$$那我们能不能直接将$P(y=1|\mathbf{x})$看作$y$带入上式来构成逻辑回归模型呢？即：
$$P(y=1|\mathbf{x})=\mathbf{w}?\mathbf{x}+b$$这样显然不合理，因为等式的左边为概率，取值应该为$0\le P(y=1|\mathbf{x})\le 1$，而等式右边的取值范围为$[?\infty ,+\infty ]$。所以应该找一个函数，将等式右边的取值范围从$[?\infty ,+\infty ]$映射到$[0,1]$上，这个函数就是sigmoid函数，其数学表达式如下，其函数图像见下图：
$$\sigma (\mathbf{z})=\frac{1}{1+\text{exp}(?z)}=\frac{\text{exp}(z)}{1+\text{exp}(z)}$$

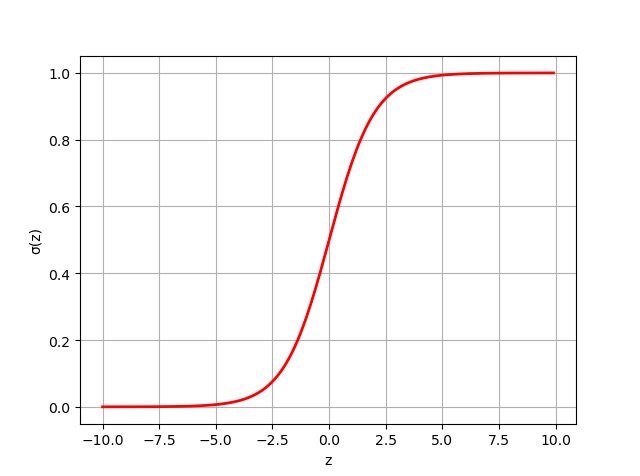
将等式的右边作为$z$带入到sigmoid函数中，便得到了逻辑回归模型：
$$\begin{gathered} P(y=1|\mathbf{x})=\frac{\text{exp}(\mathbf{w}?\mathbf{x}+b)}{1+\text{exp}(\mathbf{w}?\mathbf{x}+b)} \\ P(y=0|\mathbf{x})=\frac{1}{1+\text{exp}(\mathbf{w}?\mathbf{x}+b)} \end{gathered}$$有了模型之后，接下来我们就要讨论如何求解模型参数$\mathbf{w}$和$b$，为了后面推导方便，我们将参数模型参数$\mathbf{w}$和$b$合并为一个向量,还是记为$\mathbf{w}$，同时为了保持维度一致，将输入向量也进行扩充即：
$$\begin{gathered} \mathbf{w}=(w^{(1)},w^{(2)},...,w^{(n)}),b{)}^T \\ \mathbf{x}=(x^{(1)},x^{(2)},...,x^{(n)},1{)}^T \end{gathered}$$此时，逻辑回归模型就可以写为：
$$\begin{gathered} P(y=1|\mathbf{x})=\sigma (\mathbf{x})=\frac{\text{exp}(\mathbf{w}?\mathbf{x})}{1+\text{exp}(\mathbf{w}?\mathbf{x})} \\ P(y=0|\mathbf{x})=1?\sigma (\mathbf{x})=\frac{1}{1+\text{exp}(\mathbf{w}?\mathbf{x})} \end{gathered}$$

3.损失函数

3.1 交叉熵损失函数

??为了求解模型的最优参数，我们首先要找到合适的损失函数，并极小化损失函数，当损失最小时，此时的参数就是最优参数。我们首先想到的是线性回归所使用的损失函数，即均方误差：
$$L(\mathbf{w})=\frac{1}{2}\sum _{i=1}^N(\sigma ({\mathbf{x}}_i)?y_i{)}^2$$但是逻辑回归处理的是分类问题，$y_i$不是0就是1，而不是线性回归中的连续的数，所以均方误差在这里可能是一个非凸函数，则如下图所示，图片来源于吴恩达的机器学习课程的笔记，图中的$J(\theta )$为损失函数。这就意味着损失函数有很多局部最小值，无法确保能通过梯度下降算法找到全局最优值。

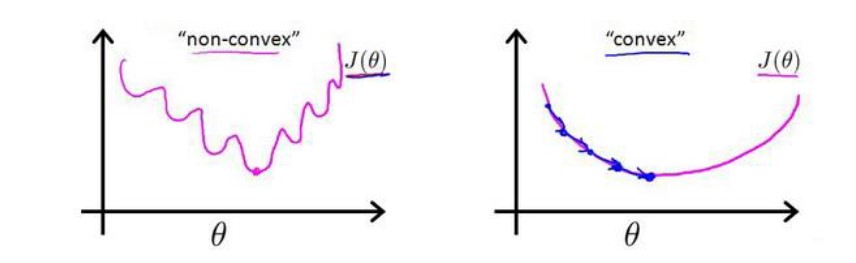
所以均方误差将不适用于逻辑回归模型。

??实际上，逻辑回归使用的是交叉熵损失函数，其数学表达式如下：
$$L(\mathbf{w})=\sum _{i=1}^N[?y_i\text{ln}(\sigma ({\mathbf{x}}_i))?(1?y_i)\text{ln}(1?\sigma ({\mathbf{x}}_i))]$$交叉熵损失函数的特点就是：当样本真实标签$y_i=1$时，损失函数第二项就为0，逻辑回归模型的输出$\sigma ({\mathbf{x}}_i)$越接近1，则损失越小，当$\sigma ({\mathbf{x}}_i)=1$时，损失为0；同理，当样本真实标签$y_i=0$时，损失函数第一项就为0，逻辑回归模型的输出$\sigma ({\mathbf{x}}_i)$越接近0，则损失越小，当$\sigma ({\mathbf{x}}_i)=0$时，损失为0。交叉熵损失函数被广泛应用于分类任务中，不仅适用于二分类，而且适用于多分类。

3.2 从极大似然估计角度理解损失函数

??其实也可以从极大似然估计的角度来理解逻辑回归模型的损失函数。首先，我们写出模型的似然函数：
$$\prod _{i=1}^N[\sigma ({\mathbf{x}}_i){]}^{y_i}[1?\sigma ({\mathbf{x}}_i{)}^{1?y_i}]$$则对数似然函数为：
$$L(\mathbf{w})=\sum _{i=1}^N[y_i\text{ln}(\sigma ({\mathbf{x}}_i))+(1?y_i)\text{ln}(1?\sigma ({\mathbf{x}}_i))]$$可以发现对数似然函数就是负的交叉熵损失函数。其实二者的意思相同，只不过从损失函数的角度，我们是要极小化损失函数，而从极大似然估计的角度，我们是要使对数似然函数最大。后面的公式推导中，我们将采用极小化交叉熵损失函数求解模型参数。

4.模型参数求解

4.1 梯度下降法

??为了求导方便，我们首先对损失函数进行化简：
$$\begin{gathered} L(\mathbf{w})=?\sum _{i=1}^N[y_i\text{ln}(\sigma ({\mathbf{x}}_i))+(1?y_i)\text{ln}(1?\sigma ({\mathbf{x}}_i)] \\ =?\sum _{i=1}^N[y_i\text{ln}(\frac{\sigma ({\mathbf{x}}_i)}{1?\sigma ({\mathbf{x}}_i)})+\text{ln}(1?\sigma ({\mathbf{x}}_i))] \\ =?\sum _{i=1}^N[y_i\text{ln}(\text{exp}(\mathbf{w}?\mathbf{x}))+\text{ln}(\frac{1}{1+\text{exp}(\mathbf{w}?\mathbf{x})})] \\ =?\sum _{i=1}^N[y_i(\mathbf{w}?\mathbf{x})?\text{ln}(1+\text{exp}(\mathbf{w}?\mathbf{x}))] \end{gathered}$$下面开始求$L(\mathbf{w})$对$\mathbf{w}$的梯度：
$$\begin{gathered} {?}_{\mathbf{w}}L(\mathbf{w})=?\sum _{i=1}^N(y_i{\mathbf{x}}_i?\frac{\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}{1+\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}{\mathbf{x}}_i) \\ =?\sum _{i=1}^N(y_i?\frac{\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}{1+\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}){\mathbf{x}}_i \\ =\sum _{i=1}^N(\frac{\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}{1+\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}?y_i){\mathbf{x}}_i \\ =\sum _{i=1}^N(\sigma ({\mathbf{x}}_i)?y_i){\mathbf{x}}_i \end{gathered}$$有了梯度之后就可以利用梯度下降来更新模型参数了，即：
$$\mathbf{w}=\mathbf{w}?\eta {?}_{\mathbf{w}}L(\mathbf{w})$$其中，$\eta$表示学习率。梯度下降的代码如下：

 #训练，梯度下降
    def train(self, train_data, train_label):
        print("start to train")
        for iter in range(self.max_iter):
            #用for循环一行一行的实现梯度下降
            for i in range(len(train_data)):
                x = np.array([train_data[i]])
                y = train_label[i]
                wx = np.dot(x, self.w)
                self.w -= self.learning_rate*(np.exp(wx)/ ( 1 + np.exp(wx))) - y) * x.T

            #直接用矩阵实现
            #计算 w*x
            # wx = np.dot(train_data, self.w)
            # #计算梯度
            # gradient = np.dot(train_data.T, (self.sigmoid(wx) - train_label))
            # #更新权值
            # self.w -= self.learning_rate*gradient
        print("training completed")
        print("w is {}".format(self.w))

4.2 牛顿法

??牛顿法的原理可以参考李航《统计学习方法》的附录B部分，这里就不详述了。利用牛顿法更新模型参数的公式如下：
$$\mathbf{w}=\mathbf{w}?H^{?1}{?}_{\mathbf{w}}L(\mathbf{w})$$其中H使Hessian矩阵，Hessian矩阵即一阶梯度${?}_{\mathbf{w}}L(\mathbf{w})$对${\mathbf{w}}^T$的梯度，其求解公式如下：
$$\begin{gathered} H={?}_{{\mathbf{w}}^T}({?}_{\mathbf{w}}L(\mathbf{w})) \\ ={?}_{{\mathbf{w}}^T}(\sum _{i=1}^N(\sigma ({\mathbf{x}}_i)?y_i){\mathbf{x}}_i) \\ ={?}_{{\mathbf{w}}^T}(\sum _{i=1}^N(\frac{\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}{1+\text{exp}(\mathbf{w}?{\mathbf{x}}_i)}){\mathbf{x}}_i) \\ =\sum _{i=1}^N{\mathbf{x}}_i^T(\frac{\text{exp}(\mathbf{w}?{\mathbf{x}}_i)(1+\text{exp}(\mathbf{w}?{\mathbf{x}}_i))?\text{exp}(\mathbf{w}?{\mathbf{x}}_i{)}^2}{[1+\text{exp}(\mathbf{w}?{\mathbf{x}}_i){]}^2}){\mathbf{x}}_i \\ =\sum _{i=1}^N{\mathbf{x}}_i^T\sigma ({\mathbf{x}}_i)(1?\sigma ({\mathbf{x}}_i)){\mathbf{x}}_i \end{gathered}$$上述求导过程中用到了列向量对行向量的导数，在《矩阵理论》课程里有讲到。
??求得Hessian矩阵后便可以对模型参数进行更新了，代码如下：

 #训练,牛顿法
    def train(self, train_data, train_label):
        print("start to train")
        for iter in range(self.max_iter):
            #一行一行的求解
            for i in range(len(train_data)):
                # 因为取出的x是个1维数组，无法进行转置，所以将其扩充为2维
                x = np.array([train_data[i]])
                y = train_label[i]
                wx = np.dot(x, self.w)
                #计算一阶导数
                gradient = np.dot(x.T, (self.sigmoid(wx) - y))
                #计算Hessian矩阵
                Hessian = np.dot(x.T, self.sigmoid(wx)).dot((1 - self.sigmoid(wx))).dot(x)
                #权值更新
                self.w -= self.learning_rate * np.linalg.pinv(Hessian).dot(gradient)
        print("training completed")
        print("w is {}".format(self.w))

5.参考资料

1.李航《统计学习方法》
2.https://www.cnblogs.com/veraLin/p/10003400.html
3.https://www.sohu.com/a/270954377_777125
4.https://github.com/fengdu78/lihang-code

推荐阅读：
SMO算法求解支持向量机的理论推导与代码实现
机器学习算法——支持向量机(3)
机器学习算法——支持向量机(2)
机器学习算法——支持向量机(1)

也欢迎大家关注我的公众号：MyLearningNote