[数据结构与算法]408数据结构——绪论&复杂度分析

绪论&复杂度分析

考纲内容

• • 数据结构与算法的基本概念
• • 算法复杂度的分析和计算

要求内容

• • 理解数据结构与算法的基本概念
• • 会分析和计算复杂度

• 思维导图索引
  

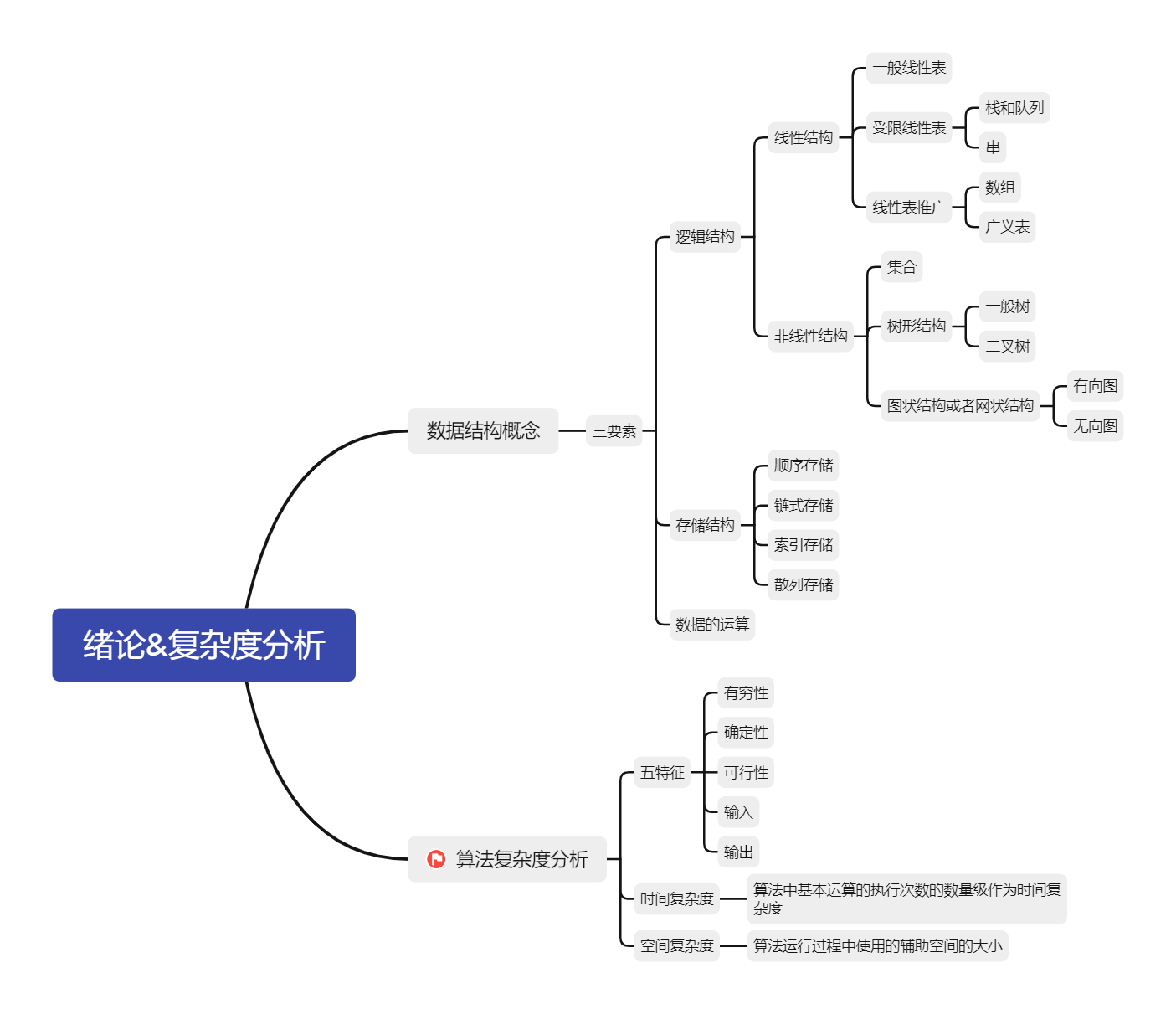
1.数据结构概念

• 数据结构是相互之间存在一种或多种特定关系数据元素的集合。

1.1 数据

• 数据是信息的载体

1.2 数据元素

• 数据元素是数据的基本单位
• 一个数据元素可由若干个数据项组成
• 数据项是构成数据元素的不可分割的最小单位
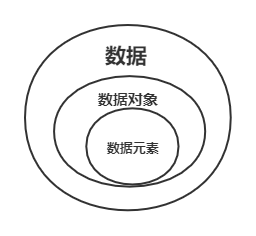
  结构关系图如下：数据 > 数据对象 > 数据元素

1.3 数据类型

• 原子类型。其值不可再分的数据类型。如：int
• 结构类型。其值可以再分解成若干成分的数据类型。如：struct结构体
• 抽象数据类型。抽象数据组织与之相关的操作

1.4 数据结构

• 数据结构是相互之间存在一种或多种特定关系数据元素的集合
• 任何问题中，数据元素都不是孤立存在的，之间存在某种特定的关系，这种数据元素相互之间的关系称为结构
• 逻辑结构、存储结构、数据的运算

1.5 数据结构三要素

1.5.1 数据的逻辑结构

?从逻辑关系上描述·数据结构，与数据的存储无关
?逻辑结构分为线性结构和非线性结构
?典型的线性结构——线性表
?典型的非线性结构——集合、树、图

分类如下

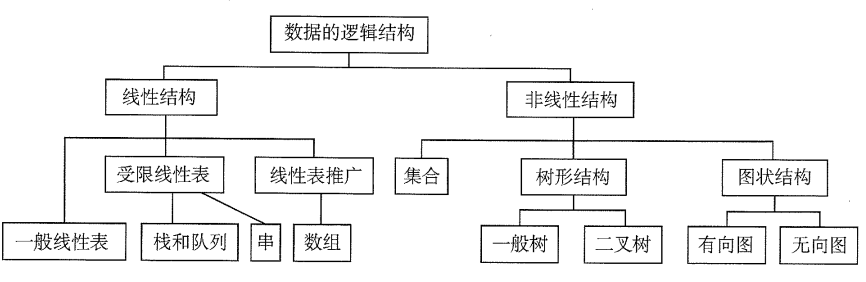
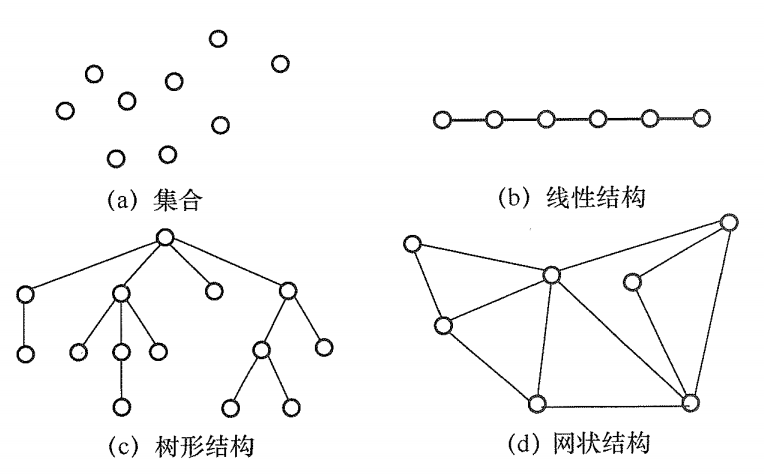
• 集合：同属一个集合，别无其他关系，如图(a)
• 线性结构：结构中的数据元素只存在一对一关系，如图(b)
• 树形结构：结构中的数据元素存在一对多关系，如图?
• 图状或者网状结构：结构中的数据元素存在多对多关系，如图(d)
  

1.5.2 数据的存储结构

• 存储结构是数据结构在计算机中的表示（也称映像），又称物理结构。它包括数据元素的表示和关系的表示
• 数据的存储结构主要有顺序存储、链式存储、索引存储和散列存储

• 顺序存储

逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，物理位置即信息在计算机中的位置，元素关系由存储单元的邻接关系体现

优点

可以实现随机存储，每个元素占最少的存储空间

缺点

只能使用相邻的一整块存储单元，如果存储连续的几个数据，可能会出现较多的未利用的空间

• 链式存储

不要求逻辑上相邻的元素在物理位置上也相邻，可以借助指示元素存储地址的指针来表示元素之间的逻辑关系

优点

不会出现碎片现象，能充分利用所有存储单元

缺点

每个元素因为存储指针而占用额外存储空间，没有上一个指针的地址找不到下一个，只能实现顺序存取

• 索引存储

在存储元素信息的同时，还建立附加的索引表，分别存放数据元素和元素间关系的存储方式，索引表每项称为索引项,索引项的一般形式是（关键字，地址）以后可以联系操作系统的文件系统章节来理解

优点

检索速度快

缺点

附加的索引表额外占用存储空间，增加和删除数据也要修改索引表，花费时间。

• 散列存储
  根据元素的关键字直接计算出该元素的存储地址，又称哈希存储

优点

检索、增加、删除结点的操作都很快

缺点

若散列函数不好，可能会出现元素存储单元的冲突。而解决冲突会增加时间和空间的开销

1.5.3 数据的运算

包括运算的定义和实现。运算的定义是针对逻辑结构的，指出运算的功能。运算的实现是针对存储结构的，指出运算的具体操作步骤。

2. 算法的基本概念和评价

算法（Algorithm）是对特定问题求解步骤的一种描述，指令的有限序列，其中每一条指令表示一个或多个操作

2.1 算法的五个重要特性

• 有穷性

有限步骤后结束，每一步都可在有穷时间内完成

• 确定性

算法中每条指令必须有确切的含义，不存在二义性，即没有歧义

• 可行性

比如受限于计算机的计算能力，有些算法虽然理论上可行，但实际上无法完成。

• 输入

一个算法有一个或多个输入

• 输出

一个算法有一个或多个输出

此外设计一个好的算法应该还要考虑以下4个目标

(1)正确性：算法能够正确的解决求解问题

(2)可读性：算法具有良好的可读性，以便帮助理解

(3)健壮性：输入非法数据时，算法能适当的做出反应或处理，而不会产生莫名奇妙的结果

(4)效率与低存储量需求：效率指的是算法执行的时间，
   存储量需求是指算法执行过程中所需要的最大存储空间，这两者都与问题的规模有关

2.2 算法的时间复杂度

所有语句的频度（执行次数）之和记为 $T(n)$ ，时间复杂度主要分析 $T(n)$ 的数量级，通常采用算法中基本运算的频度（执行次数）来分析时间复杂度。因此,算法的时间复杂度记为$$T(n)=O(f(n))$$例如$T(n)=n^2+n+1，T(n)=O(n^2)$
则 $O(n^2)$ 即为所求的复杂度

一般只考虑最坏情况下的时间复杂度，以保证算法的运行时间不会比它更长

• 加法规则

多项相加,只保留最高阶的项，且系数变为1

$T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))$

• 乘法规则

多项相乘，都保留

$T(n)=T_1\times T_2(n)=O(f(n))\times O(g(n))=O(f(n)\times g(n))$

• Eg:

$T_3(n)=n^3+n^{2}lo{g}_{2}n$

$=O(n^3)+O(n^{2}lo{g}_{2}n)$
$=O(max((n^3,n^{2}lo{g}_{2}n))$
$=O(n^3)$

• 常见渐近时间复杂度

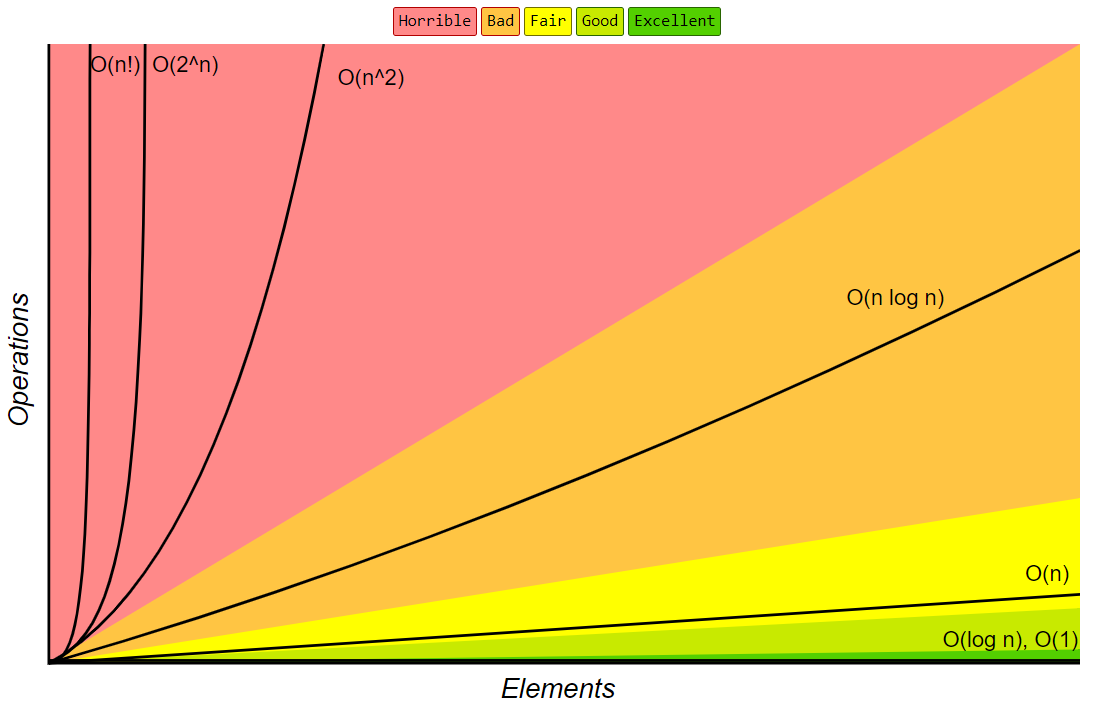
$O(1)<O(lo{g}^{2}n)<O(n)<O(nlo{g}^{2}n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$
速记方式：常对幂指阶

渐近线如下

2.2 算法的空间复杂度

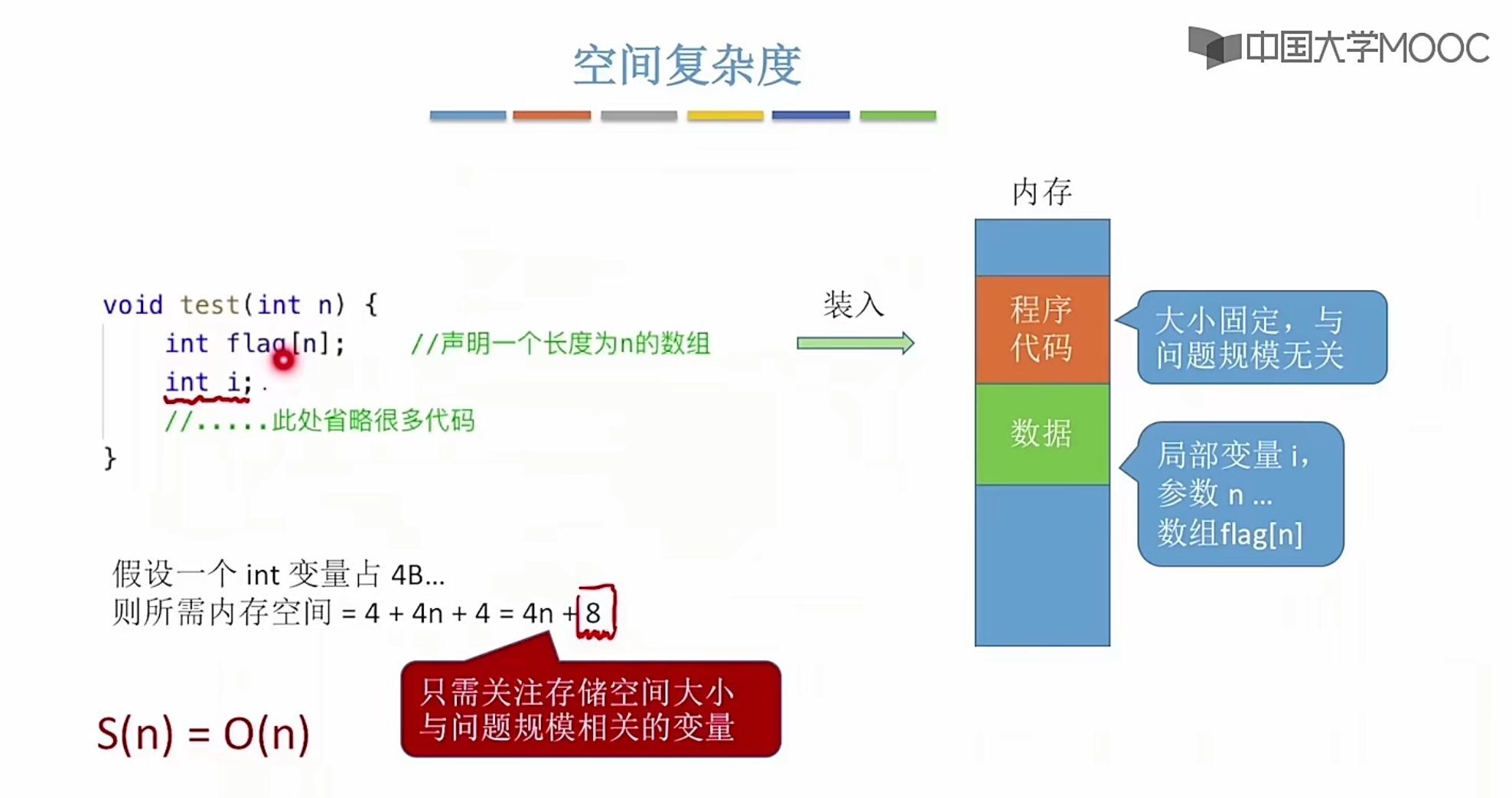
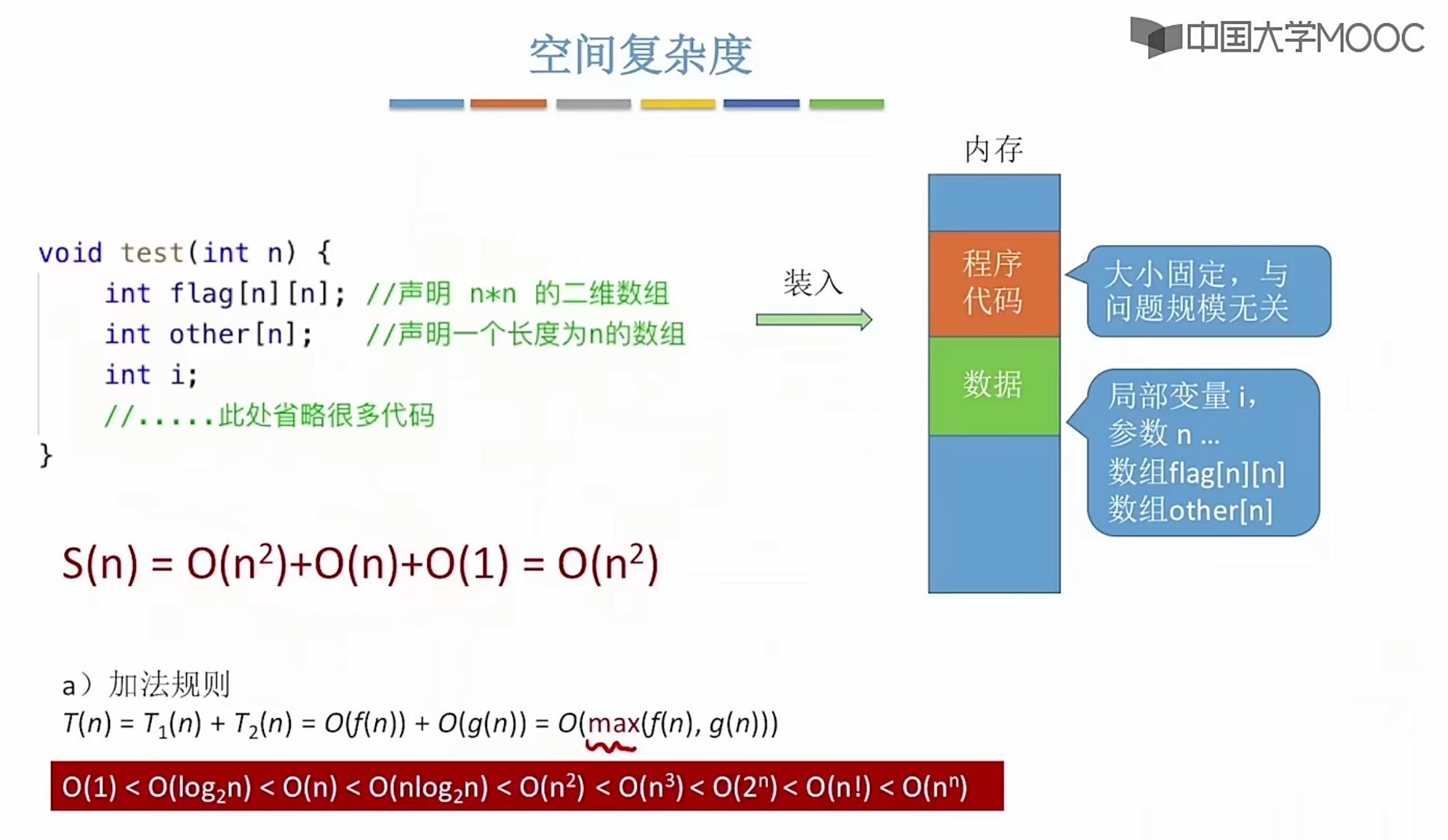
• 算法的空间复杂度 $S(n)$定义为该算法所消耗的存储空间，她是问题规模 $n$ 的函数，它用来衡量算法随着问题规模增大，算法所需空间的快慢；记为$$S(n)=O(g(n))$$
• 算法运行过程中使用的辅助空间的大小,所占的空间只取决于问题本身，和算法无关，只需要分析除输入和程序之外的额外空间
• 算法原地工作是指算法所需辅助空间是常量，即 $O(1)$

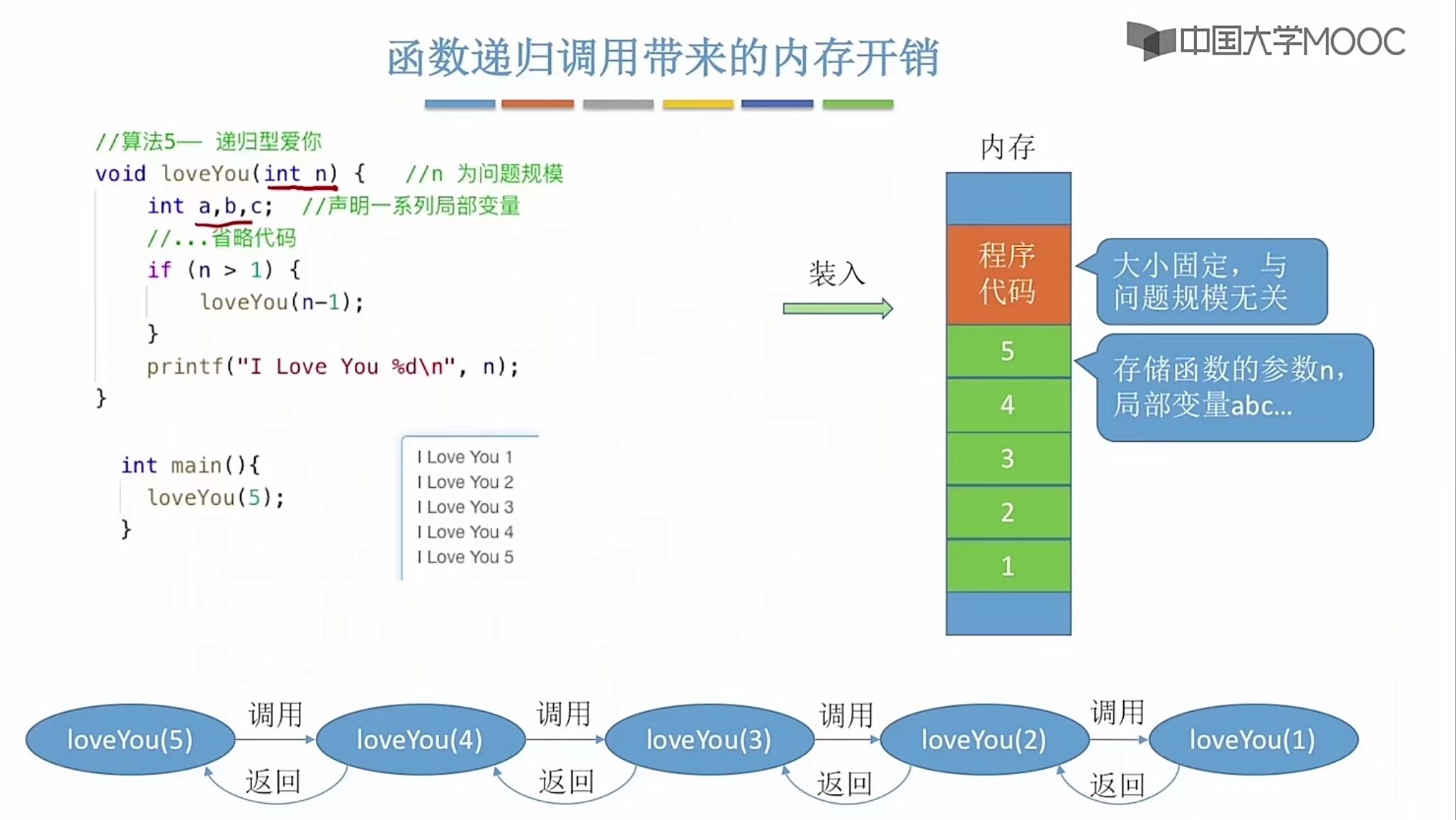
王道课程里讲的空间复杂度题目

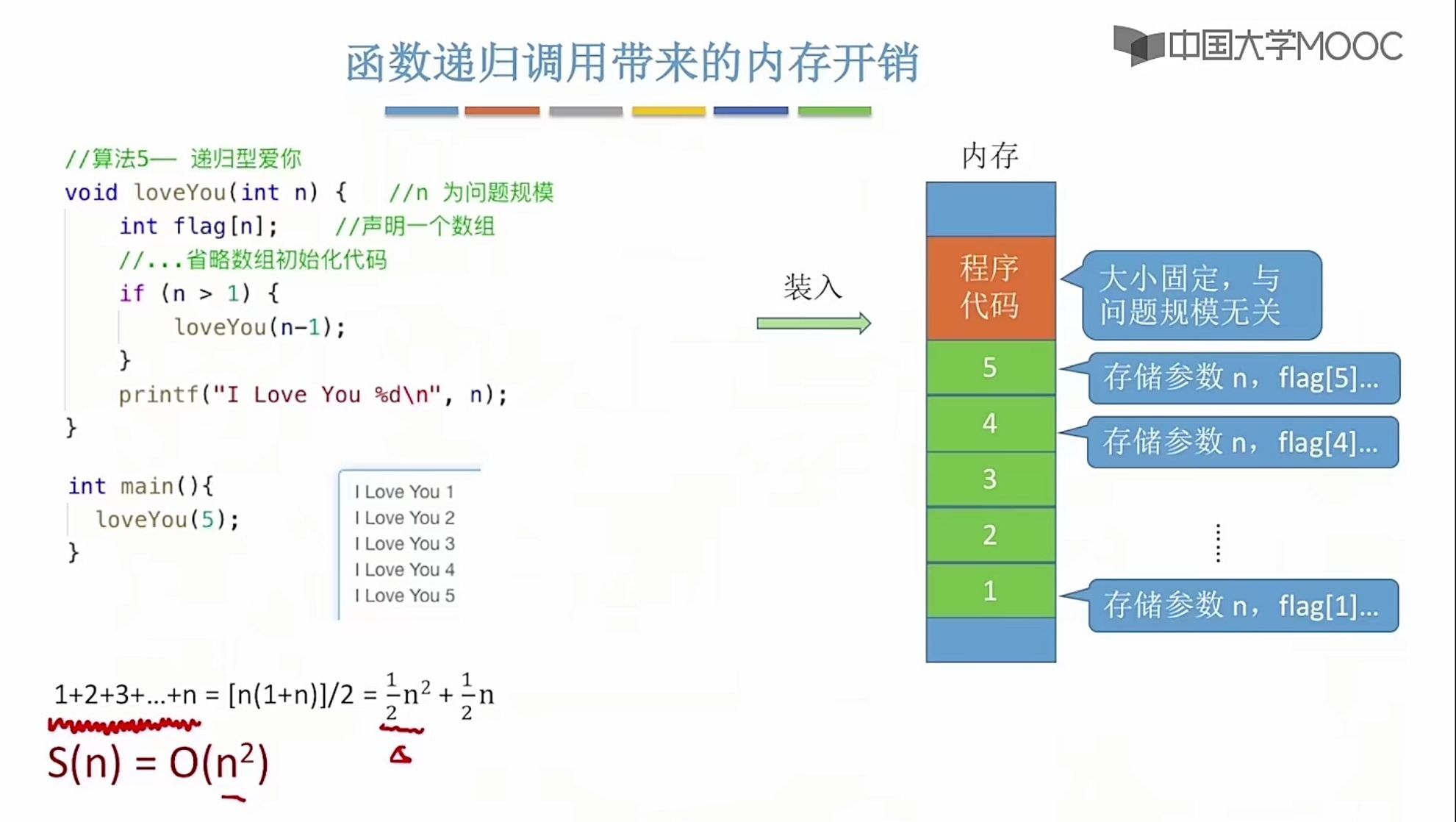
2.3 复杂度题型总结

2.3.1 循环主体中的变量参与循环条件的判断

此类题应该中出主体语句中与 $T(n)$ 成正比的循环变量，将之代入条件中计算。例如：

1. int i=1;       2.  int y=5;   
   while(i<=n)        while((y+1)*(y+1)<n)
   		i=i*2;		  y=y+1;

例 1 中, $i$ 乘以 $2$ 的次数正是主体语句的执行次数 $t$ ，因此 $2^t?n$，取对数后得 $t<lo{g}_{2}n$,则$T(n)=O(lo{g}_{2}n)$

例 2 中， $y$ 加 $1$的次数恰好与$T(n)$成正比，记 $t$ 为该程序的执行次数并令 $t=y?5$，有$y=t+5$,$(t+5+1)\times (t+5+1)<n$ ，得$t<\sqrt{n}?6$,即 $T(n)=O(\sqrt{n})$

2.3.2 循环主体中的变量与循环条件无关

此类题可用数学归纳法或者直接累计循环次数。多层循环从内到外分析，忽略单步语句、条件判断语句，只关注主体语句的执行次数。此类问题又可以分为递归程序和非递归程序：

• 递归程序一般使用公式进行递推,例如

【2012统考】求整数 $n(n\geq0)$ 的阶乘算法如下，
其时间复杂度是______

int fact(int n) {
	if( n<=1)	return 1;
	return n*fact(n-1);
}

本题求的是阶乘 $n!$ 的递归代码，每次递归调用时 fact () 的参数减一，时间复杂度分析如下：$$T(n)=1+T(n?1)=1+1+T(n?2)=???=n?1+T(1)$$递归出口为 fact(1),一共执行n次递归调用 fact() ，故复杂度为$T(n)=O(n)$

• 非递归程序比较简单，可以直接累计次数，例如

【2017统考真题】下列函数时间复杂度是_____

int func(int n){
	int i=0,sum=0;
	while(sum<n) sum+=++i;
	return i;
}

基本运算 sum+=++i，它等价 ++i ；sum = sum+i，每执行一次 i 自增 1， i=1 时，sum=0+1;
i=2 时，sum=0+1+2；以此类推得出$$sum=0+1+2+???+i=(1+i)?i/2$$,可知循环次数满足 $t$ 满足 (1+t) * t/2<n，因此时间复杂度为$O(n^{1/2})$

2.3.3 运用公式法求时间复杂度例题

void func(int n)
{
	int i,j,x=0;
	for (i=1;i<n;i++)
		for(j=i+1;j<=n;j++)
			x++;
}

思路：

• 先确定主体语句，主体语句是 x++，复杂度为$O(1)$

  • 确定外层循环，因为$i<n$，外层循环从 $1$ 到 $n?1$，$$\sum _{i=1}^{n?1}$$

  ---

• 确定内层循环，因为$j<n$，外层循环从 $1$ 到 $n?1$，$$\sum _{i=1}^{n?1}$$

  • 确定内层循环，$j?n$,内层循环从 $i+1$ 到 $n$ ,$$\sum _{j=i+1}^n$$

• 则$$\sum _{i=1}^{n?1}\sum _{j=i+1}^{n}1$$

计算过程如下图

对于$n?(i+1)+1$可能有些疑惑，为什么要$+1$,其实就是一个累加计数的过程，下面给出解释

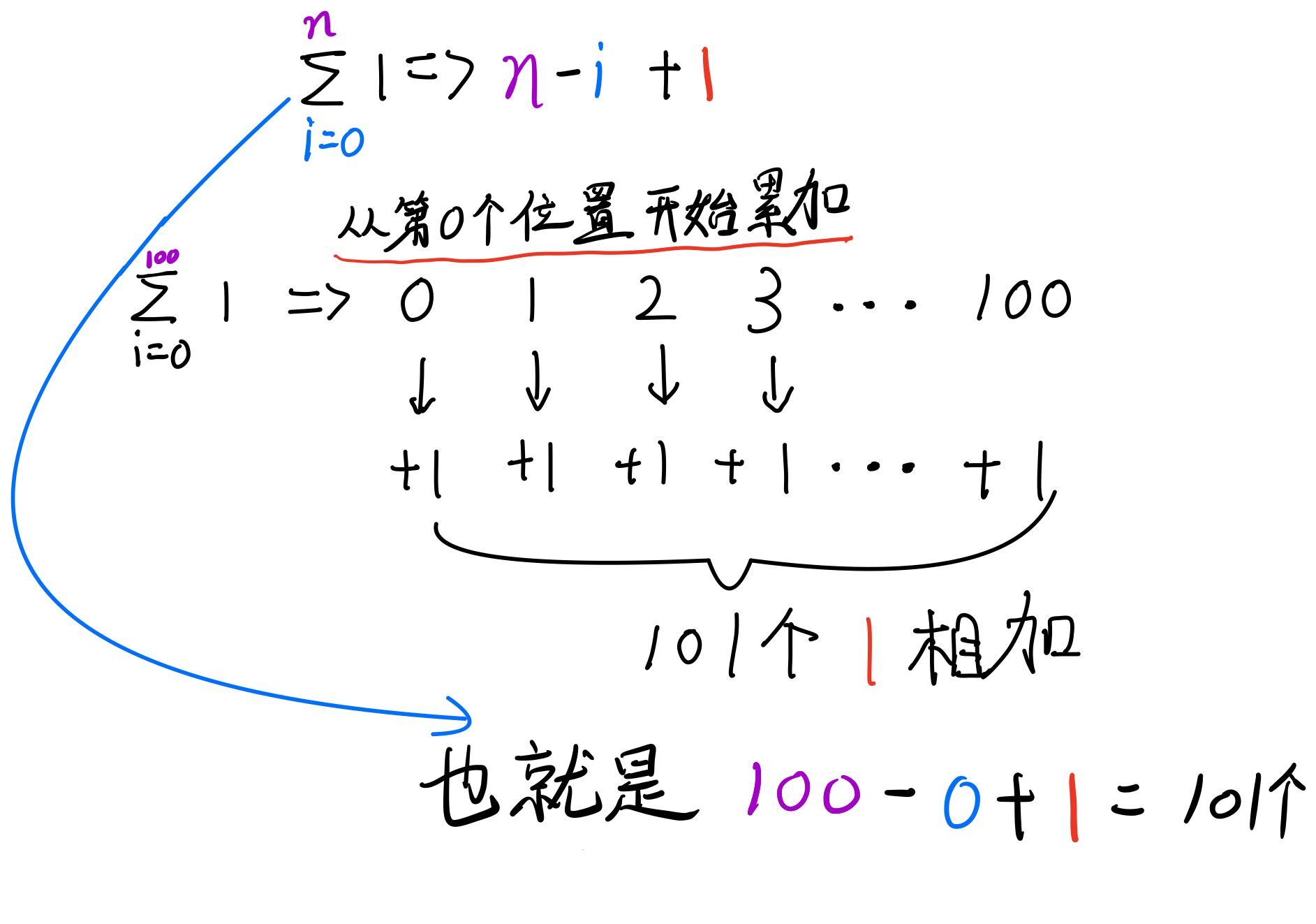
$0$ 的位置到 $100$ 的位置总共有 $101$ 个位置，每个位置自增$+1$，也就是$101$个$1$相加。

3. 思维拓展

求解斐波那契数列

$$F(n)=\{\begin{array}{cccc}1，n=0,1& & & \\ F(n?1)+F(n?2)，n>1& & & \end{array}$$

有两种算法：递归算法和非递归算法，试分别分析两种算法时间复杂度。

3.1递归算法

首先写出递归算法的函数

int fact(int n)
{
	if(n==0||n==1)	
		return 1;
	else
		return(fact(n-1)+fact(n-2))
}

先给出我的想法

• 当 $n?1$ 的时候，就直接return了，时间复杂度为$O(1)$

• 当 $n>1$ 的时候，调用递归函数入口fact(n-1) 和 fact(n-2),然后还要进行判断，

  • 时间复杂度为$O(1)+T(n?1)+T(n?2)$

• 接着继续进入函数调用入口，直到 $T(1)$ ,得出 $2^{n?1}O(1)$，由大O算法的数量级知，时间复杂度为 $O(2^n)$

3.2 非递归算法

非递归函数代码如下

int Fibonacci(unsigned int n)
{
	int a = 1, b = 1, c = 0;//a保存f(n-2),b保存f(n-1),c保存f(n)
	for(int i = 3; i <= n; i++)//递推求出f(i)
	{
		c = a + b;//f(n) = f(n - 1) + f(n - 2)
		a = b;//a保存b
		b = c;//b保存c
	}
	return c;
}

可以看出时间复杂度为 $O(n)$

3.2 递归算法的优点和缺点

递归优点：
1. 简洁
2. 容易理解思路清晰
3. 可以解决非线性的执行过程。
缺点：
1.递归由于是函数调用自身，而函数调用是有时间和空间的消耗的：
每一次函数调用，都需要在内存栈中分配空间以保存参数、返回地址以及临时变量，
而往栈中压入数据和弹出数据都需要时间

2.递归中很多计算都是重复的，由于其本质是把一个问题分解成两个或者多个小问题，
多个小问题存在相互重叠的部分，则存在重复计算，如fibonacci斐波那契数列的递归实现

3.调用栈可能会溢出，其实每一次函数调用会在内存栈中分配空间，
而每个进程的栈的容量是有限的，当调用的层次太多时，就会超出栈的容量，从而导致栈溢出

总结:
耗费内存、速度慢

建议：
能用循环解决的问题不要使用递归。

4.归纳一个在天勤数据结构看到的递归时间复杂度总结

本章节结束