[数据结构与算法]图的遍历（DFSBFS）

图的遍历：从图中某一顶点出发访问图中其余顶点，且每一个顶点仅被访问一次

图有2种常见的遍历方式（有向图、无向图都适用）：

1. 广度优先搜索（Breadth First Search，BFS），又称为宽度优先搜索、横向优先搜索

2. 深度优先遍历(Depth First Search, DFS)

广度优先搜索

1. 理解
   类似于树的层序遍历
   
   
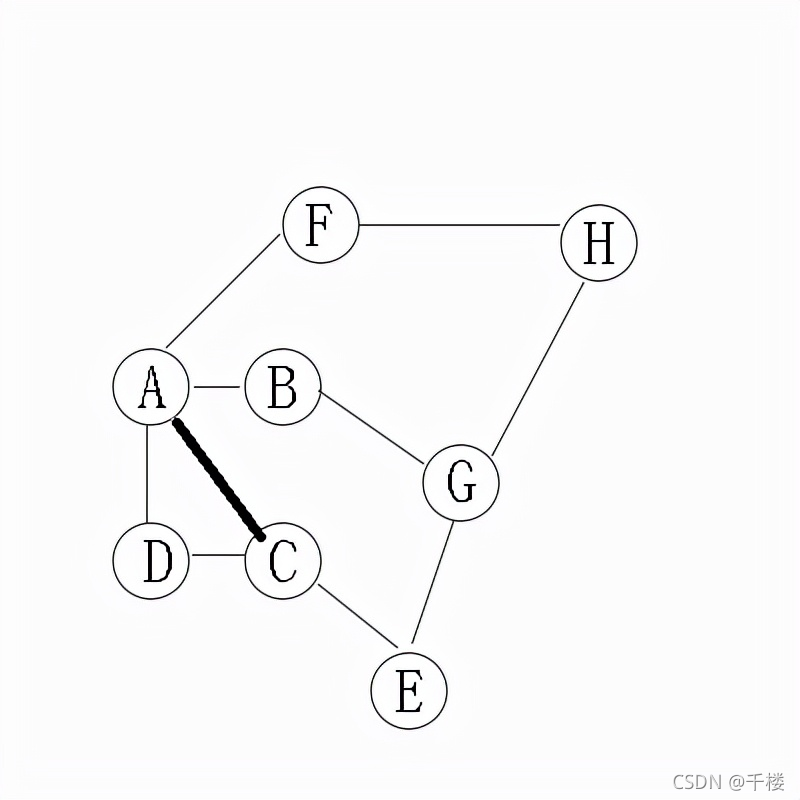
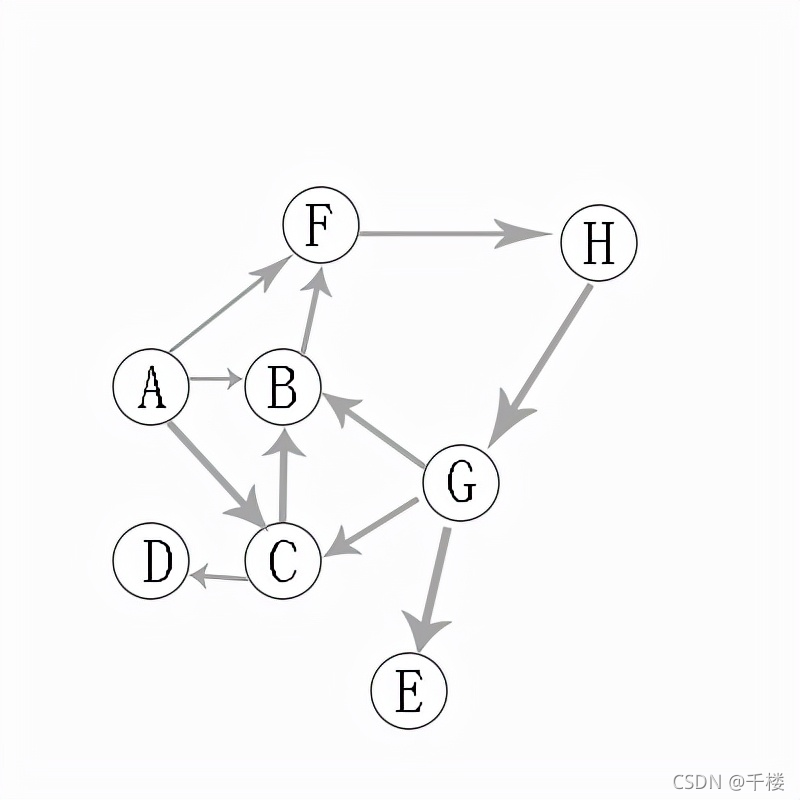
   无向图，从A点开始
   第一层： A
   第二层： B C D F
   第三层： G E H
   所以，最终的遍历顺序：A -> B -> C -> D -> F -> G -> E -> H

2）代码实现(请先学习上一篇文章：图(Grapth))：

@Override
    public void bfs(V begin, VertexVisitor visitor) {
      	//获取起点
        Vertex<V, E> beginVertex = vertices.get(begin);
        if (beginVertex == null) {
            return;
        }
      	//记录已经遍历过的节点
        Set<Vertex<V, E>> visitedVertices = new HashSet<>();
        Queue<Vertex<V, E>> queue = new LinkedList<>();
      	//将起点加入队列
        queue.offer(beginVertex);
        while (!queue.isEmpty()) {
          	//获取队列的元素
            Vertex<V, E> vertex = queue.poll();
          	//遍历
            visitor.visit(vertex.value);
          	//已经遍历过的添加到集合中记录下来
            visitedVertices.add(vertex);
          	//将该顶点的出度节点或者说以这个顶点为起点的边，遍历，获取到另外端点
            vertex.outEdges.forEach(edge -> {
              	//如果没遍历过就加入到队列中
                if (!visitedVertices.contains(edge.to)) {
                    queue.offer(edge.to);
                }
            });
        }
    }

深度优先遍历
1）理解
从一个顶点出发，沿着当前顶点的边走到未访问的顶点，直到没有未访问过的顶点时，返回上一个顶点，继续试探别的顶点，直到所有顶点都被访问过。

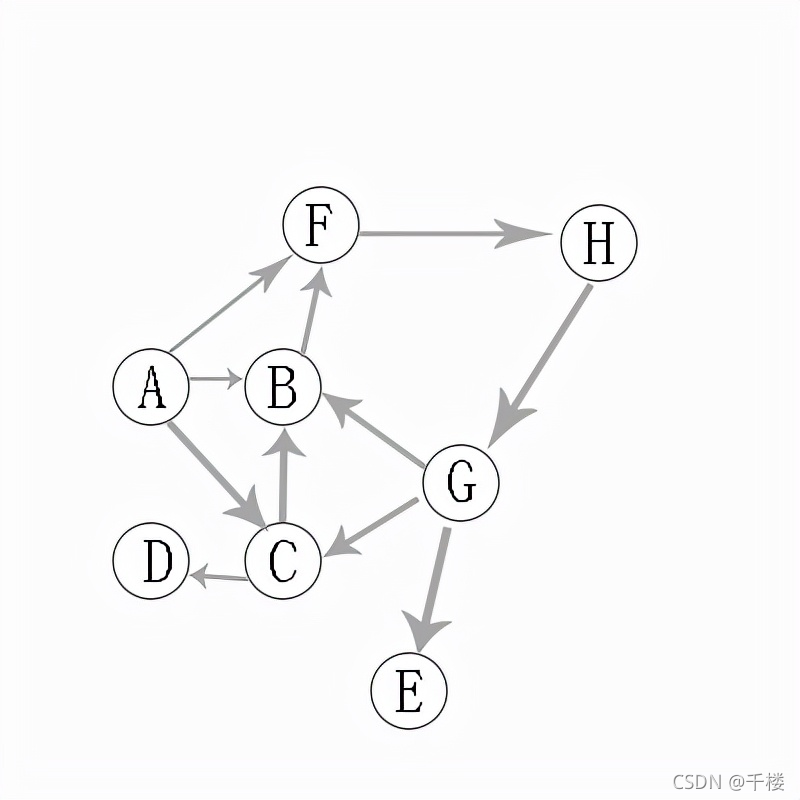
从A出发，邻接点有 B C F，假设 下一个访问节点 B，那么， A B F H G C D E
在访问到G顶点时候，可以访问的下一个节点有 C E，假设是 C ,那么就是 C D ，然后返回到G,然后继续访问E。

2）代码实现

private void dfs(Vertex<V, E> beginVertex, VertexVisitor visitor) {
    Stack<Vertex<V, E>> stack = new Stack<>();
  	//记录已经访问过的节点
    List<Vertex<V, E>> visitedVertex = new ArrayList<>();
    stack.push(beginVertex);
    visitedVertex.add(beginVertex);
    visitor.visit(beginVertex.value);
    while (!stack.isEmpty()) {
        Vertex<V, E> vertex = stack.pop();
        vertex.outEdges.forEach(edge -> {
          	//没有访问过的
            if (!visitedVertex.contains(edge.to)) {
                stack.push(vertex);
                stack.push(edge.to);
                visitedVertex.add(edge.to);
                visitor.visit(edge.to.value);
            }
        });
    }
}