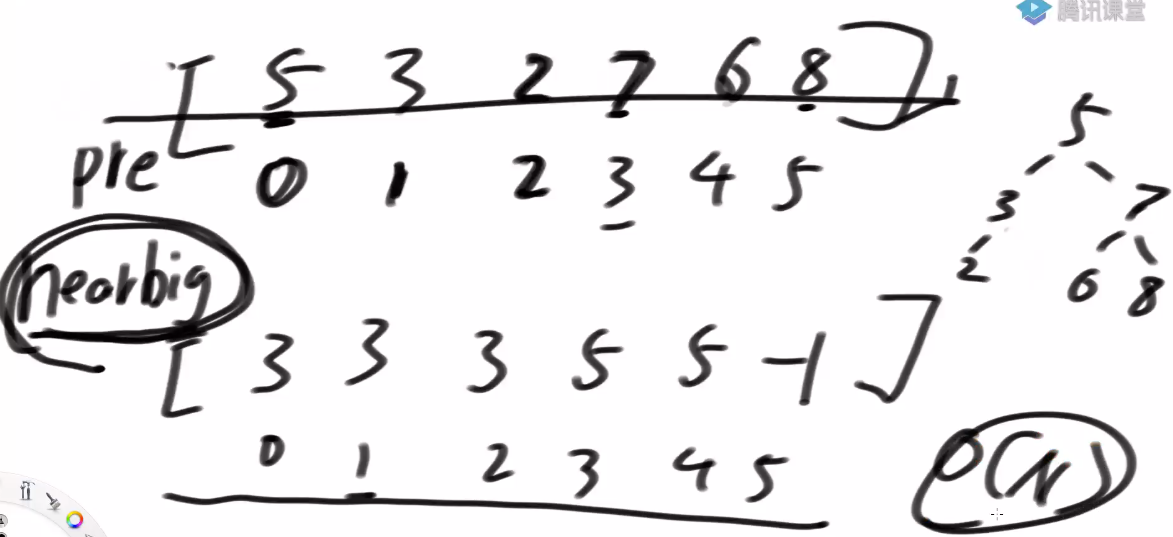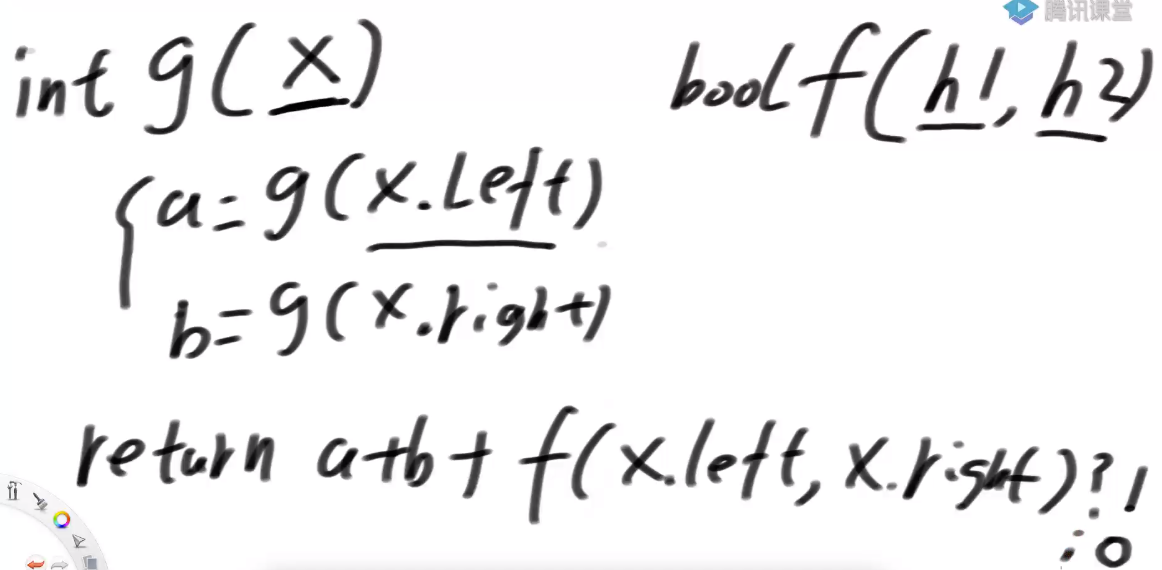题目一
已知一棵搜索二叉树上没有重复值的节点,
现在有一个数组arr,是这棵搜索二叉树先序遍历的结果
请根据arr生成整棵树并返回头节点
https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/
解题:
方法一:递归思想,定义函数f(L,R),从L....R范围是一棵树的先序遍历结果,请建出整颗树把头部node返回
方法二: 使用单调栈,生成nearBig数组,跟原来数组等长,复杂度O(N)
0位置的数的右边离他最近的,比它大的那个位置?3位置
1位置的数的右边离他最近的,比它大的那个位置?3位置
2位置的数的右边离他最近的,比它大的那个位置?3位置
3位置的数的右边离他最近的,比它大的那个位置?5位置
4位置的数的右边离他最近的,比它大的那个位置?5位置
5位置的数的右边离他最近的,比它大的那个位置?-1位置
有这个辅助数组,再去处理上面的f函数,就不需要遍历了,这个辅助记录可以直接告诉我在哪儿
public static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode() {
}
public TreeNode(int val) {
this.val = val;
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public static TreeNode bstFromPreorder1(int[] pre) {
if (pre == null || pre.length == 0) {
return null;
}
return process1(pre, 0, pre.length - 1);
}
public static TreeNode process1(int[] pre, int L, int R) {
if (L > R) {
return null;
}
int firstBig = L + 1;
for (; firstBig <= R; firstBig++) {
if (pre[firstBig] > pre[L]) {
break;
}
}
TreeNode head = new TreeNode(pre[L]);
head.left = process1(pre, L + 1, firstBig - 1);
head.right = process1(pre, firstBig, R);
return head;
}// 已经是时间复杂度最优的方法了,但是常数项还能优化
public static TreeNode bstFromPreorder2(int[] pre) {
if (pre == null || pre.length == 0) {
return null;
}
int N = pre.length;
int[] nearBig = new int[N];
for (int i = 0; i < N; i++) {
nearBig[i] = -1;
}
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < N; i++) {
while (!stack.isEmpty() && pre[stack.peek()] < pre[i]) {
nearBig[stack.pop()] = i;
}
stack.push(i);
}
return process2(pre, 0, N - 1, nearBig);
}
public static TreeNode process2(int[] pre, int L, int R, int[] nearBig) {
if (L > R) {
return null;
}
int firstBig = (nearBig[L] == -1 || nearBig[L] > R) ? R + 1 : nearBig[L];
TreeNode head = new TreeNode(pre[L]);
head.left = process2(pre, L + 1, firstBig - 1, nearBig);
head.right = process2(pre, firstBig, R, nearBig);
return head;
}// 最优解
public static TreeNode bstFromPreorder3(int[] pre) {
if (pre == null || pre.length == 0) {
return null;
}
int N = pre.length;
int[] nearBig = new int[N];
for (int i = 0; i < N; i++) {
nearBig[i] = -1;
}
int[] stack = new int[N];
int size = 0;
for (int i = 0; i < N; i++) {
while (size != 0 && pre[stack[size - 1]] < pre[i]) {
nearBig[stack[--size]] = i;
}
stack[size++] = i;
}
return process3(pre, 0, N - 1, nearBig);
}
public static TreeNode process3(int[] pre, int L, int R, int[] nearBig) {
if (L > R) {
return null;
}
int firstBig = (nearBig[L] == -1 || nearBig[L] > R) ? R + 1 : nearBig[L];
TreeNode head = new TreeNode(pre[L]);
head.left = process3(pre, L + 1, firstBig - 1, nearBig);
head.right = process3(pre, firstBig, R, nearBig);
return head;
}题目二
?如果一个节点X,它左树结构和右树结构完全一样
那么我们说以X为头的树是相等树
给定一棵二叉树的头节点head
返回head整棵树上有多少棵相等子树
解题:
?定义函数:给定一个节点h1,再给我一个h2,告诉你h1的结构和h2的结构相不相等;再定义一个整体的g函数,以x为头节点的整棵树有多少个相等的子树
// 时间复杂度O(N * logN)
public static int sameNumber1(Node head) {
if (head == null) {
return 0;
}
return sameNumber1(head.left) + sameNumber2(head.right) + (same(head.left, head.right) ? 1 : 0);
}
public static boolean same(Node h1, Node h2) {
if (h1 == null ^ h2 == null) {
return false;
}
if (h1 == null && h2 == null) {
return true;
}
// 两个都不为空
return h1.value == h2.value && same(h1.left, h2.left) && same(h1.right, h2.right);
}优化:
把左树跟右数比对的这个过程,可以将O(N)--->O(1)
将左树和右树信息,使用hashcode表示,这样只需要比较hash值,就可以确定其是不是相等,hashcode值是一个等长的字符串,这样可以将比较过程降低到O(1)
// 时间复杂度O(N)
public static int sameNumber2(Node head) {
String algorithm = "SHA-256";
Hash hash = new Hash(algorithm);
return process(head, hash).ans;
}
public static class Info {
public int ans;
public String str;
public Info(int a, String s) {
ans = a;
str = s;
}
}
public static Info process(Node head, Hash hash) {
if (head == null) {
return new Info(0, hash.hashCode("#,"));
}
Info l = process(head.left, hash);
Info r = process(head.right, hash);
int ans = (l.str.equals(r.str) ? 1 : 0) + l.ans + r.ans;
String str = hash.hashCode(String.valueOf(head.value) + "," + l.str + r.str);
return new Info(ans, str);
}题目三
?编辑距离问题
两个字符串,如何使用一定的编辑手段,使得两个字符串相等
场景的编辑动作有4中:1)保留 代价0? 2)删除? 代价a? ?3)添加? ?代价b? ?4)替换? 代价c
解题:
dp[i][j]:str1的前缀取i个字符,编辑成str2前缀取j个字符最少代价是多少??
可能性1):str1的前i-1个字符编程str2的前j个字符,即删掉str1的最后一个字符
可能性2):str1的整体先变成str2的前j-1个字符,最后再加上str2的最后一个字符
可能性3):str1,str2两个字符串最后一个字符相等,str1前面i-1个字符变成str2前面的j-1个字符,最后一个字符保留
可能性4)两个字符串的最后一个字符不相等,str1的前面i-1个字符变成str2前面j-1个字符,最后一个字符做替换
public static int minCost1(String s1, String s2, int ic, int dc, int rc) {
if (s1 == null || s2 == null) {
return 0;
}
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int N = str1.length + 1;
int M = str2.length + 1;
int[][] dp = new int[N][M];
// dp[0][0] = 0
for (int i = 1; i < N; i++) {
dp[i][0] = dc * i;
}
for (int j = 1; j < M; j++) {
dp[0][j] = ic * j;
}
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
dp[i][j] = dp[i - 1][j - 1] + (str1[i - 1] == str2[j - 1] ? 0 : rc);
dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + ic);
dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + dc);
}
}
return dp[N - 1][M - 1];
}public static int minCost2(String str1, String str2, int ic, int dc, int rc) {
if (str1 == null || str2 == null) {
return 0;
}
char[] chs1 = str1.toCharArray();
char[] chs2 = str2.toCharArray();
char[] longs = chs1.length >= chs2.length ? chs1 : chs2;
char[] shorts = chs1.length < chs2.length ? chs1 : chs2;
if (chs1.length < chs2.length) {
int tmp = ic;
ic = dc;
dc = tmp;
}
int[] dp = new int[shorts.length + 1];
for (int i = 1; i <= shorts.length; i++) {
dp[i] = ic * i;
}
for (int i = 1; i <= longs.length; i++) {
int pre = dp[0];
dp[0] = dc * i;
for (int j = 1; j <= shorts.length; j++) {
int tmp = dp[j];
if (longs[i - 1] == shorts[j - 1]) {
dp[j] = pre;
} else {
dp[j] = pre + rc;
}
dp[j] = Math.min(dp[j], dp[j - 1] + ic);
dp[j] = Math.min(dp[j], tmp + dc);
pre = tmp;
}
}
return dp[shorts.length];
}题目四
?给定两个字符串s1和s2,问s2最少删除多少字符可以成为s1的子串?
比如 s1 = "abcde",s2 = "axbc"
?解题:
dp[i][j]表示,x的0...i-1字符只通过删除方式变成y的0...j-1个字符,
可能性1):两个字符串不相等,删掉最后一个字符,指望x从0....i-2的字符变成y的字符
可能性2):两个字符串相等,可以删掉x前面的字符变成y,或者保留x前面的字符变成y前面的字符
// 解法一
// 求出str2所有的子序列,然后按照长度排序,长度大的排在前面。
// 然后考察哪个子序列字符串和s1的某个子串相等(KMP),答案就出来了。
// 分析:
// 因为题目原本的样本数据中,有特别说明s2的长度很小。所以这么做也没有太大问题,也几乎不会超时。
// 但是如果某一次考试给定的s2长度远大于s1,这么做就不合适了。
public static int minCost1(String s1, String s2) {
List<String> s2Subs = new ArrayList<>();
process(s2.toCharArray(), 0, "", s2Subs);
s2Subs.sort(new LenComp());
for (String str : s2Subs) {
if (s1.indexOf(str) != -1) { // indexOf底层和KMP算法代价几乎一样,也可以用KMP代替
return s2.length() - str.length();
}
}
return s2.length();
}
public static void process(char[] str2, int index, String path, List<String> list) {
if (index == str2.length) {
list.add(path);
return;
}
process(str2, index + 1, path, list);
process(str2, index + 1, path + str2[index], list);
}
public static class LenComp implements Comparator<String> {
@Override
public int compare(String o1, String o2) {
return o2.length() - o1.length();
}
}// x字符串只通过删除的方式,变到y字符串
// 返回至少要删几个字符
// 如果变不成,返回Integer.Max
public static int onlyDelete(char[] x, char[] y) {
if (x.length < y.length) {
return Integer.MAX_VALUE;
}
int N = x.length;
int M = y.length;
int[][] dp = new int[N + 1][M + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= M; j++) {
dp[i][j] = Integer.MAX_VALUE;
}
}
dp[0][0] = 0;
// dp[i][j]表示前缀长度
for (int i = 1; i <= N; i++) {
dp[i][0] = i;
}
for (int xlen = 1; xlen <= N; xlen++) {
for (int ylen = 1; ylen <= Math.min(M, xlen); ylen++) {
if (dp[xlen - 1][ylen] != Integer.MAX_VALUE) {
dp[xlen][ylen] = dp[xlen - 1][ylen] + 1;
}
if (x[xlen - 1] == y[ylen - 1] && dp[xlen - 1][ylen - 1] != Integer.MAX_VALUE) {
dp[xlen][ylen] = Math.min(dp[xlen][ylen], dp[xlen - 1][ylen - 1]);
}
}
}
return dp[N][M];
}// 解法二
// 生成所有s1的子串
// 然后考察每个子串和s2的编辑距离(假设编辑距离只有删除动作且删除一个字符的代价为1)
// 如果s1的长度较小,s2长度较大,这个方法比较合适
public static int minCost2(String s1, String s2) {
if (s1.length() == 0 || s2.length() == 0) {
return s2.length();
}
int ans = Integer.MAX_VALUE;
char[] str2 = s2.toCharArray();
for (int start = 0; start < s1.length(); start++) {
for (int end = start + 1; end <= s1.length(); end++) {
// str1[start....end]
// substring -> [ 0,1 )
ans = Math.min(ans, distance(str2, s1.substring(start, end).toCharArray()));
}
}
return ans == Integer.MAX_VALUE ? s2.length() : ans;
}
// 求str2到s1sub的编辑距离
// 假设编辑距离只有删除动作且删除一个字符的代价为1
public static int distance(char[] str2, char[] s1sub) {
int row = str2.length;
int col = s1sub.length;
int[][] dp = new int[row][col];
// dp[i][j]的含义:
// str2[0..i]仅通过删除行为变成s1sub[0..j]的最小代价
// 可能性一:
// str2[0..i]变的过程中,不保留最后一个字符(str2[i]),
// 那么就是通过str2[0..i-1]变成s1sub[0..j]之后,再最后删掉str2[i]即可 -> dp[i][j] = dp[i-1][j] + 1
// 可能性二:
// str2[0..i]变的过程中,想保留最后一个字符(str2[i]),然后变成s1sub[0..j],
// 这要求str2[i] == s1sub[j]才有这种可能, 然后str2[0..i-1]变成s1sub[0..j-1]即可
// 也就是str2[i] == s1sub[j] 的条件下,dp[i][j] = dp[i-1][j-1]
dp[0][0] = str2[0] == s1sub[0] ? 0 : Integer.MAX_VALUE;
for (int j = 1; j < col; j++) {
dp[0][j] = Integer.MAX_VALUE;
}
for (int i = 1; i < row; i++) {
dp[i][0] = (dp[i - 1][0] != Integer.MAX_VALUE || str2[i] == s1sub[0]) ? i : Integer.MAX_VALUE;
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
dp[i][j] = Integer.MAX_VALUE;
if (dp[i - 1][j] != Integer.MAX_VALUE) {
dp[i][j] = dp[i - 1][j] + 1;
}
if (str2[i] == s1sub[j] && dp[i - 1][j - 1] != Integer.MAX_VALUE) {
dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1]);
}
}
}
return dp[row - 1][col - 1];
}
// 解法二的优化
public static int minCost3(String s1, String s2) {
if (s1.length() == 0 || s2.length() == 0) {
return s2.length();
}
char[] str2 = s2.toCharArray();
char[] str1 = s1.toCharArray();
int M = str2.length;
int N = str1.length;
int[][] dp = new int[M][N];
int ans = M;
for (int start = 0; start < N; start++) { // 开始的列数
dp[0][start] = str2[0] == str1[start] ? 0 : M;
for (int row = 1; row < M; row++) {
dp[row][start] = (str2[row] == str1[start] || dp[row - 1][start] != M) ? row : M;
}
ans = Math.min(ans, dp[M - 1][start]);
// 以上已经把start列,填好
// 以下要把dp[...][start+1....N-1]的信息填好
// start...end end - start +2
for (int end = start + 1; end < N && end - start < M; end++) {
// 0... first-1 行 不用管
int first = end - start;
dp[first][end] = (str2[first] == str1[end] && dp[first - 1][end - 1] == 0) ? 0 : M;
for (int row = first + 1; row < M; row++) {
dp[row][end] = M;
if (dp[row - 1][end] != M) {
dp[row][end] = dp[row - 1][end] + 1;
}
if (dp[row - 1][end - 1] != M && str2[row] == str1[end]) {
dp[row][end] = Math.min(dp[row][end], dp[row - 1][end - 1]);
}
}
ans = Math.min(ans, dp[M - 1][end]);
}
}
return ans;
}// 复杂度和方法三一样,但是思路截然不同
public static int minCost4(String s1, String s2) {
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
HashMap<Character, ArrayList<Integer>> map1 = new HashMap<>();
for (int i = 0; i < str1.length; i++) {
ArrayList<Integer> list = map1.getOrDefault(str1[i], new ArrayList<Integer>());
list.add(i);
map1.put(str1[i], list);
}
int ans = 0;
// 假设删除后的str2必以i位置开头
// 那么查找i位置在str1上一共有几个,并对str1上的每个位置开始遍历
// 再次遍历str2一次,看存在对应str1中i后续连续子串可容纳的最长长度
for (int i = 0; i < str2.length; i++) {
if (map1.containsKey(str2[i])) {
ArrayList<Integer> keyList = map1.get(str2[i]);
for (int j = 0; j < keyList.size(); j++) {
int cur1 = keyList.get(j) + 1;
int cur2 = i + 1;
int count = 1;
for (int k = cur2; k < str2.length && cur1 < str1.length; k++) {
if (str2[k] == str1[cur1]) {
cur1++;
count++;
}
}
ans = Math.max(ans, count);
}
}
}
return s2.length() - ans;
}