[数据结构与算法]排序算法 ---- 快速排序

一、快排简介

快速排序借助了分治的思想，它的基本思想是:

1. 选定一个关键字 key ，通过一次排序，将其放到整个序列排序完毕的位置，并且他的左序列小于等于 key。
   右序列大于等于 key 。

2. 递归地将分割出的两个子序列继续进行第一步排序。

图示：

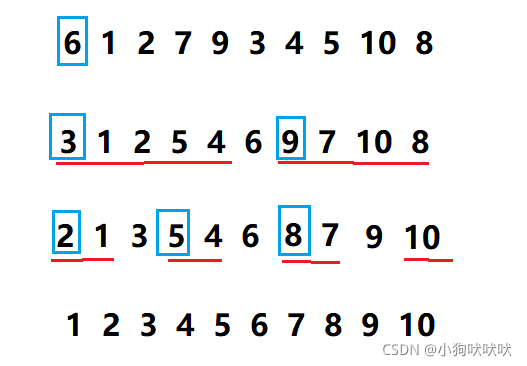
二、部分排序

1. Hoare法

默认选定 left 为keyi。 从右边找一个比key小的元素，左边找一个比key大的元素，交换两元素。当 left == right 相等。此时它们所在位置就为key最终排序所在位置。 交换 key 和 left。

注意点：

关键字选 left 。得让right先找。这样才能保证正确。如果关键字选 right ，反之。

代码示例：

int PartSort1(int* arr, int left, int right)
{
	int keyi = left;

	while (left < right)
	{
		while (left < right && arr[right] >= arr[keyi])
			right--;
		while (left < right && arr[left] <= arr[keyi])
			left++;
		Swap(&arr[left], &arr[right]);
	}
	Swap(&arr[keyi], &arr[left]);
	return left;
}

2.hole法

代码示例：

int PartSort2(int* arr, int left, int right)
{
	int hole = left;
	int key = arr[hole];

	while (left < right)
	{
		while (left < right && arr[right] >= key)
			right--;

		arr[hole] = arr[right];
		hole = right;

		while (left < right && arr[left] <= key)
			left++;

		arr[hole] = arr[left];
		hole = left;
	}

	arr[hole] = key;
	return hole;
}

3. 双指针法

1. prev指向下标为0元素， cur 指向下标为1元素。
2. cur往后走，如果 arr[cur] 小于 key ，prev++,并交换prev 和 cur 所在元素。
3. 迭代结束，prev所在位置为key最终位置。

代码示例：

int PartSort3(int* arr, int left, int right)
{
	int cur = 1, prev = 0;
	int keyi = left;

	while (cur <= right)
	{
		if (arr[cur] <= arr[keyi] && ++prev != cur)
			Swap(&arr[cur], &arr[prev]);
		++cur;
	}

	Swap(&arr[prev], &arr[keyi]);
	return prev;
}

三、递归实现

当left >= right 时，说明待排区间最多只有一个元素，默认就是有序，无需排序了。

代码示例：

void QuickSort(int* arr, int left, int right)
{
	if (right <= left)
		return;

	int keyi = PartSort1(arr, left, right);

	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1, right);
}

运行截图：

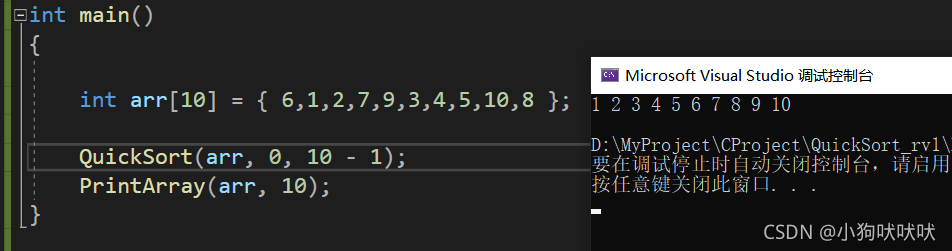
四、排序优化

前面我们key的选择一直为待排序列最左边数。但在待排序列有序或接近有序的情况下效率会变得非常低下。

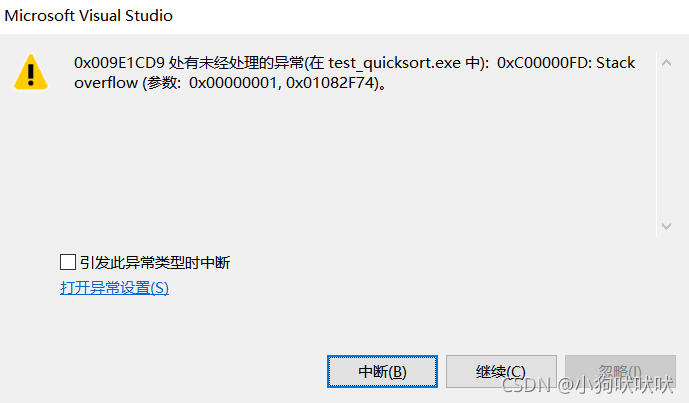
问题示例：

当数组有序时，此时平均复杂为O(N^2) ，进行一万个数排序栈就溢出了。

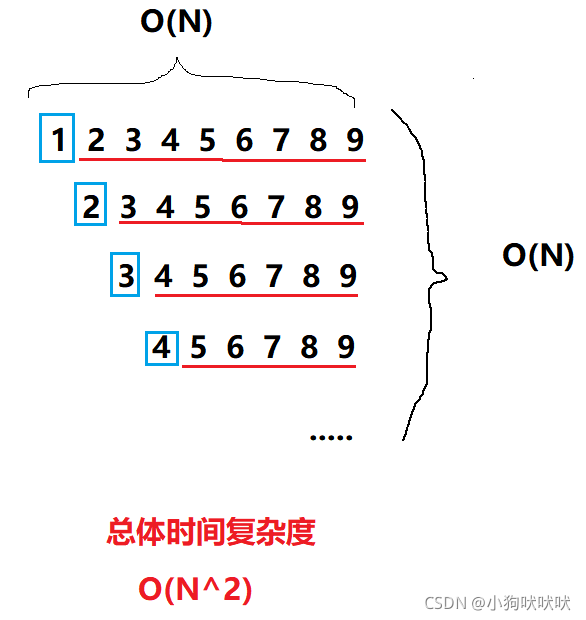
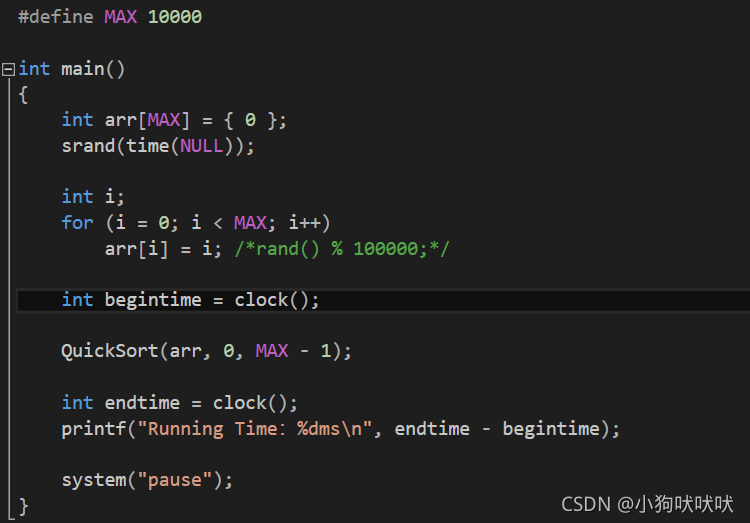
当待排数组内为随机数时，效率又恢复到了O(N * logN) 。十万个数也很快的排序完成。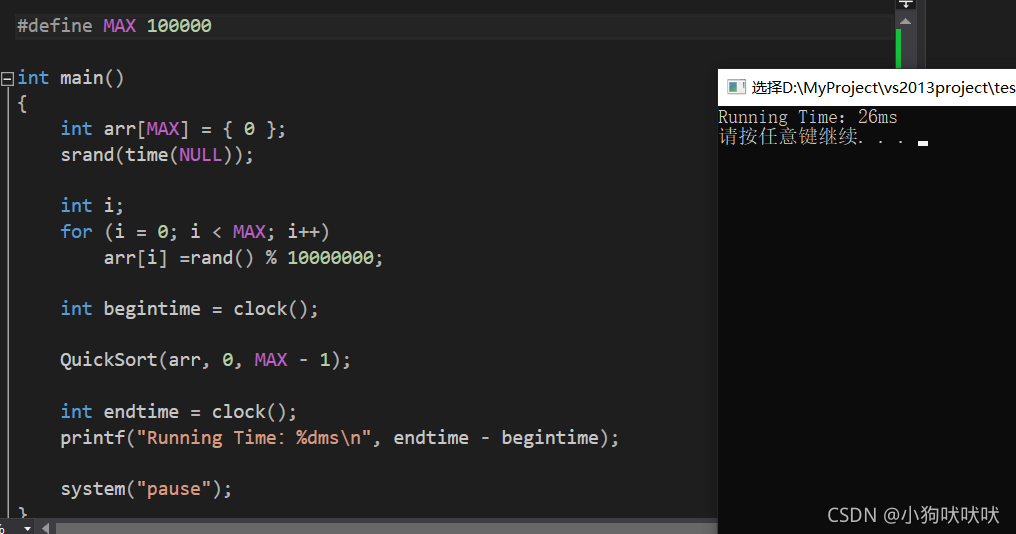

解决方法：

1. 取随机数。

2. 三数取中法 ，在left right mid 三个下标指向的数中取中位数。

代码示例：

int PartSort1(int* arr, int left, int right)
{
	//三位取中 当待排序列有序的时候也有效
	int mid = GetMid(arr, left, right);
	Swap(&arr[left], &arr[mid]);
	int keyi = left;

	while (left < right)
	{
		while (left < right && arr[right] >= arr[keyi])
			right--;
		while (left < right && arr[left] <= arr[keyi])
			left++;
		Swap(&arr[left], &arr[right]);
	}
	Swap(&arr[keyi], &arr[left]);
	return left;
}

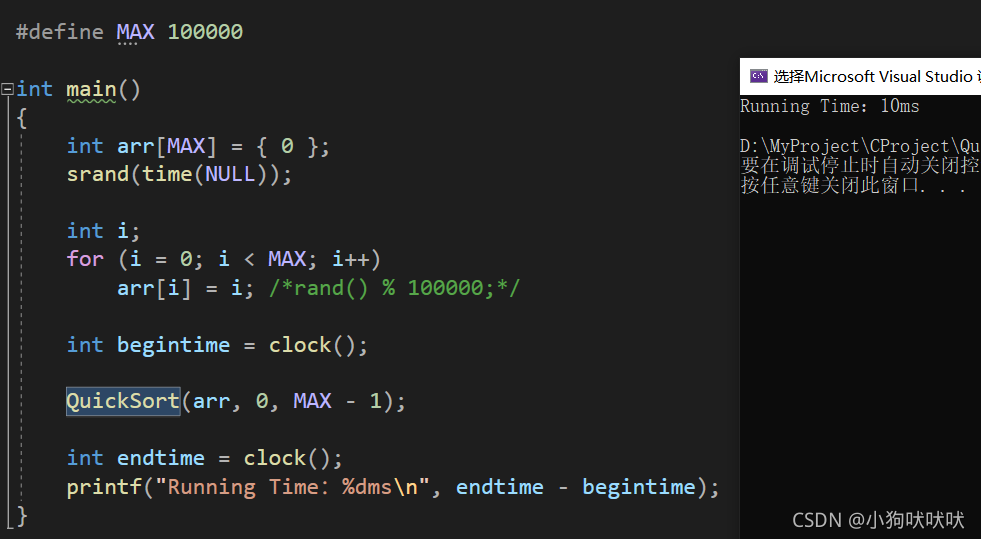
此时十万个有序序列进行排序也可以保证效率。

.