1. 理论推导
假设三维空间中有三个点P1(x1,y1,z1), P2(x2,y2,z2), P3(x3,y3,z3)三个点构成一个三角形,另外有两个点Q(xq,yq,zq),R(xr,yr,zr)构成一条空间线段。那么怎么获得线段和三角形面的交点坐标呢?我们可以假设线段的坐标用参数方程表示:
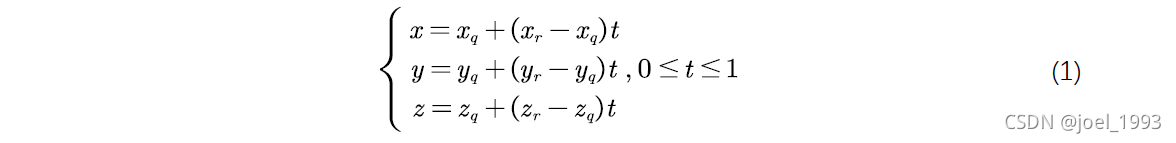
然后三角形所在平面的方程用行列式表示为
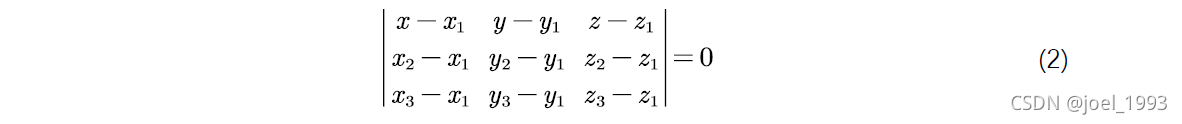
?联立这两个方程,可以解出线段参数方程t的值,判断其是否落在[0,1]区间中,如果落在其中,那么必然有交点,且交点可以由方程(1)获得。
然后关键的是求出的交点是不是在三角形内部,这里用的是交点与三角形的三个顶点所构成的三个三角形的面积之和,是否等于整个原先的大三角形面积来确定的,即面积法。
2. 数值实现
作者熟练使用MATLAB软件求解问题,故而数值实现全部使用MATLAB工具。其实原理知道了,哪种语言都可以的。
2.1 t的符号解
直接给出符号求解的代码:
syms t xq yq zq x1 y1 z1 x2 y2 z2 x3 y3 z3 alpha beta gamma
x = xq + alpha*t;
y = yq + beta*t;
z = zq + gamma*t;
A = [x,y,z,1; x1,y1,z1,1; x2,y2,z2,1; x3,y3,z3,1];
t = solve(det(A),t)这里我将alpha=xr-xq; beta=yr-yq; gamma=zr-zq代换了,表达式会简便一点。然后你可以得到一个老长的t关于xq、yq、zq、x1、y1、z1、x2、y2、z2、x3、y3、z3、alpha、beta、gamma的表达式:
t = -(x1*y2*z3 - x1*y3*z2 - x2*y1*z3 + x2*y3*z1 + x3*y1*z2 - ...
x3*y2*z1 - x1*y2*zq + x1*yq*z2 + x2*y1*zq - x2*yq*z1 - xq*y1*z2 +...
xq*y2*z1 + x1*y3*zq - x1*yq*z3 - x3*y1*zq + x3*yq*z1 + xq*y1*z3 - ...
xq*y3*z1 - x2*y3*zq + x2*yq*z3 + x3*y2*zq - x3*yq*z2 - xq*y2*z3 + xq*y3*z2)...
/(beta*x1*z2 - beta*x2*z1 - beta*x1*z3 + beta*x3*z1 + beta*x2*z3 -...
beta*x3*z2 - alpha*y1*z2 + alpha*y2*z1 + alpha*y1*z3 - alpha*y3*z1 -...
alpha*y2*z3 + alpha*y3*z2 - gamma*x1*y2 + gamma*x2*y1 + gamma*x1*y3 -...
gamma*x3*y1 - gamma*x2*y3 + gamma*x3*y2)可以看出来是一个分母,一个分子,两个部分组成,因为分母不能等于0,所以要把分母先计算出来,其实分母等于0也很好理解,那就是线段跟平面平行了。
2.1 求交点函数
我这里就不多说了,直接贴代码
function cp = crossTriSeg(p_tri, p_seg, isPlot)
% Wan Ji, Wuhan University, 2021-9-23
% p_tri = [x1,y1,z1; x2,y2,z2; x3,y3,z3]即三角形三个顶点坐标
% p_seg = [xq,yq,zq; xr,yr,zr]即线段两个顶点坐标
% isPlot 一个逻辑判断,true则画图,否则不画图(方便显示)
cp = []; % 预设空交点
s_tri = norm(cross(p_tri(:,2)-p_tri(:,1), p_tri(:,3)-p_tri(:,1)));
if(det(s_tri)<eps)
error('输入的空间三角形三个顶点共线,请检查三个点的位置')
end
x1 = p_tri(1,1); y1 = p_tri(1,2); z1 = p_tri(1,3);
x2 = p_tri(2,1); y2 = p_tri(2,2); z2 = p_tri(2,3);
x3 = p_tri(3,1); y3 = p_tri(3,2); z3 = p_tri(3,3);
xq = p_seg(1,1); yq = p_seg(1,2); zq = p_seg(1,3);
xr = p_seg(2,1); yr = p_seg(2,2); zr = p_seg(2,3);
alpha = xr - xq;
beta = yr-yq;
gamma = zr-zq;
s =(beta*x1*z2 - beta*x2*z1 - beta*x1*z3 + beta*x3*z1 + ...
beta*x2*z3 - beta*x3*z2 - alpha*y1*z2 + alpha*y2*z1 + ...
alpha*y1*z3 - alpha*y3*z1 - alpha*y2*z3 + alpha*y3*z2 - ...
gamma*x1*y2 + gamma*x2*y1 + gamma*x1*y3 - gamma*x3*y1 - ...
gamma*x2*y3 + gamma*x3*y2);
if(abs(s)<eps)
error('线段所在直线和三角形平面平行,请检查输入!')
end
t = -(x1*y2*z3 - x1*y3*z2 - x2*y1*z3 + x2*y3*z1 + x3*y1*z2 - ...
x3*y2*z1 - x1*y2*zq + x1*yq*z2 + x2*y1*zq - x2*yq*z1 - ...
xq*y1*z2 + xq*y2*z1 + x1*y3*zq - x1*yq*z3 - x3*y1*zq + ...
x3*yq*z1 + xq*y1*z3 - xq*y3*z1 - x2*y3*zq + x2*yq*z3 + ...
x3*y2*zq - x3*yq*z2 - xq*y2*z3 + xq*y3*z2) / s;
if(t>1 || t<0)
fprintf('线段与三角形没有交点(三角形与线段外延长线有交点)')
return;
end
% 求得线段与平面的交点
x = xq + t*alpha;
y = yq + t*beta;
z = zq + t*gamma;
s1 = norm(cross([x-x1,y-y1,z-z1], [x-x2,y-y2,z-z2]));
s2 = norm(cross([x-x2,y-y2,z-z2], [x-x3,y-y3,z-z3]));
s3 = norm(cross([x-x3,y-y3,z-z3], [x-x1,y-y1,z-z1]));
if(abs(s1+s2+s3-s_tri)<1e-12)
cp = [x,y,z];
else
fprintf('线段与三角形没有交点(线段与三角形所在平面交点在三角形外面)')
end
if(isPlot)
h = patch(p_tri(:,1), p_tri(:,2), p_tri(:,3), rand(1,3));
set(h, 'facealpha',0.5,'edgecolor','k');
hold on
plot3(p_tri(:,1), p_tri(:,2), p_tri(:,3),'ro','markerfacecolor','r','markersize',8)
plot3(p_seg(:,1), p_seg(:,2), p_seg(:,3),'b-o','markerfacecolor','b','markersize',8)
if(~isempty(cp))
plot3(x, y, z,'go','markerfacecolor','g','markersize',5)
legend('三角形','三个顶点','线段','交点')
else
legend('三角形','三个顶点','线段')
end
view(54,22)
end
end?怎么用这个函数呢,其实很简单,只需要给出三角形的三个顶点坐标和线段的两个端点坐标即可,下面是调用这个函数的代码:
p_tri = [
1, 0, 0;
0, 1, 0;
0, 0, 1;
]; % 三角形三个顶点坐标
p_seg = [
0, 0, 0;
1, 1, 1;
]; % 线段两个端点坐标
cp = crossTriSeg(p_tri, p_seg, true) cp就是交点坐标,cp是空的,说明没交点;true是要画图结果显示(这里用了format rat显示)
cp =
1/3 1/3 1/3 可见交点坐标是(1/3,1/3,1/3)
画出的图如下
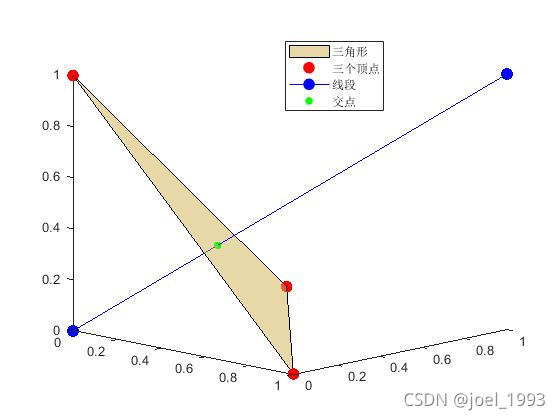
?可见交点求解成功!Enjoy!
4. 总结
本文通过线段的参数方程,以及三角形的三个顶点确定的平面方程的联合求解,根据参数t的区间判断线段和三角形的平面是否有交点,再根据面积法确定交点是否在三角形内部,得到最终的空间线段与空间三角形的坐标求解函数。
希望浏览了博主这篇文章的网友,有所收获别忘了给博主点个赞哦,有疑问可以在评论区指出呢。