前言
图论之遍历其实在之前在学习搜索的时候就已经有所学习,众所周知,要遍历一个图我们最常用的两种方法就是dfs(深度优先)和bfs(广度优先),故拓扑排序也遵循这个说法
个人定义
拓扑排序是一种按照特定方式对图的一种遍历,根据音译 top排序的想象我们容易想到用队列的顶端处理。
把AOV网(用定点表示活动,用弧表示活动间优先关系的有向图)络中各个顶点按照它们互相之间的优先关系排列成一个线性序列的过程叫做拓扑排序。
拓扑排序的适用场景
拿我们大学的课程学习进行举例,我们学了c语言学java,学了java学java高级,学了java高级和数据库学java web…如果把这些课程视作图的一个个顶点,同时告诉你某两门课程的关系,要我们整理出其顺序,该如何处理?
其实这就是我们的拓扑排序所要做的事情。
我们先跳出代码讲原理
first对图的存储:图的存储方法有很多 我们呢先采用最朴素 最有效的邻接矩阵,主要是在已知顶点的时候更方便处理。
second 寻找没有前置的顶点,即没有头的点,将其作为一个第一点,将其放入队列
third 遍历队列,每次取出队列中的一个元素,断开每个点附带的边然后这个点进入答案数组,同时判断断开边后有没有产生新的没有前置的点,若有将其放入队列。
forth 判断是否产生环:查看答案数组的长度与要排序的总点数是否相等,如果不相等说明产生了环,环在拓扑排序中是不允许存在的。
finally 下面没有了
偷了个图
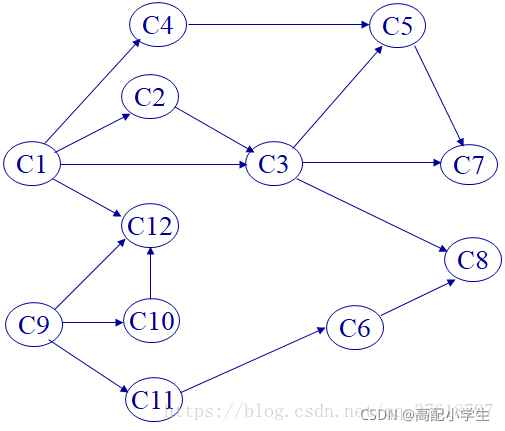
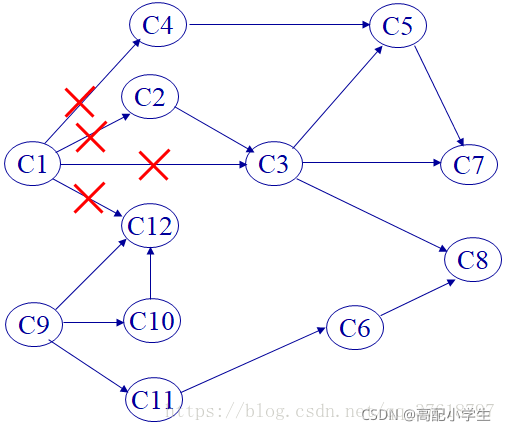
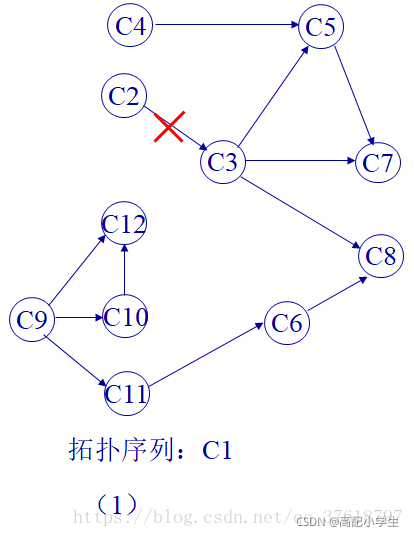
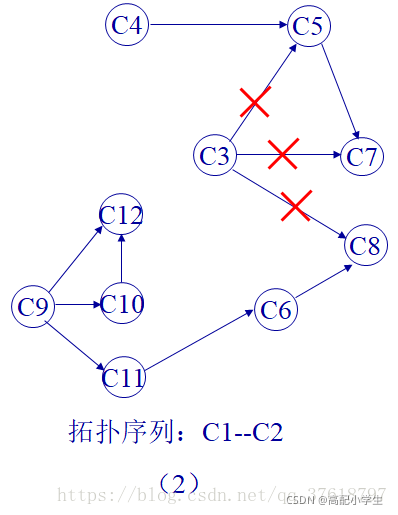
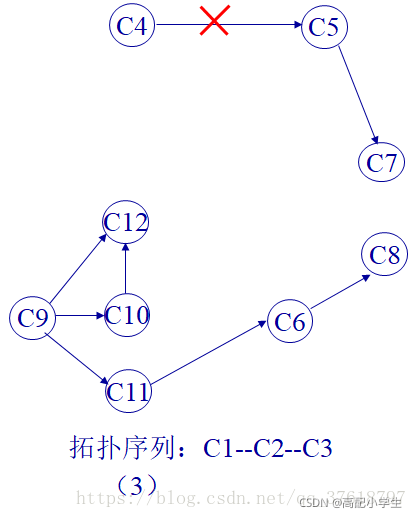
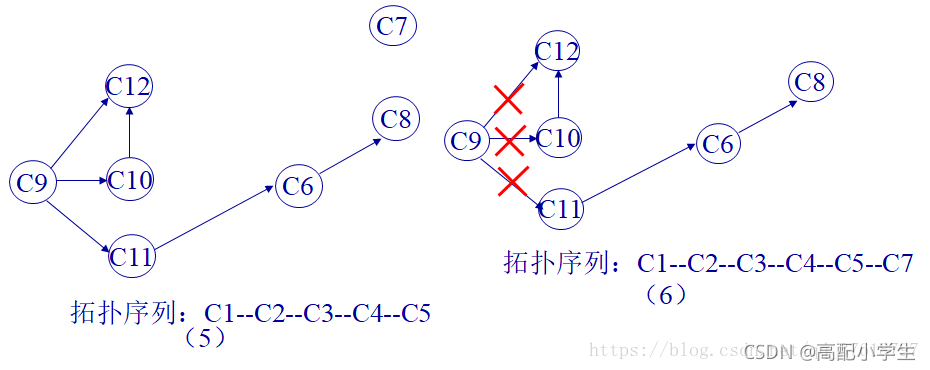

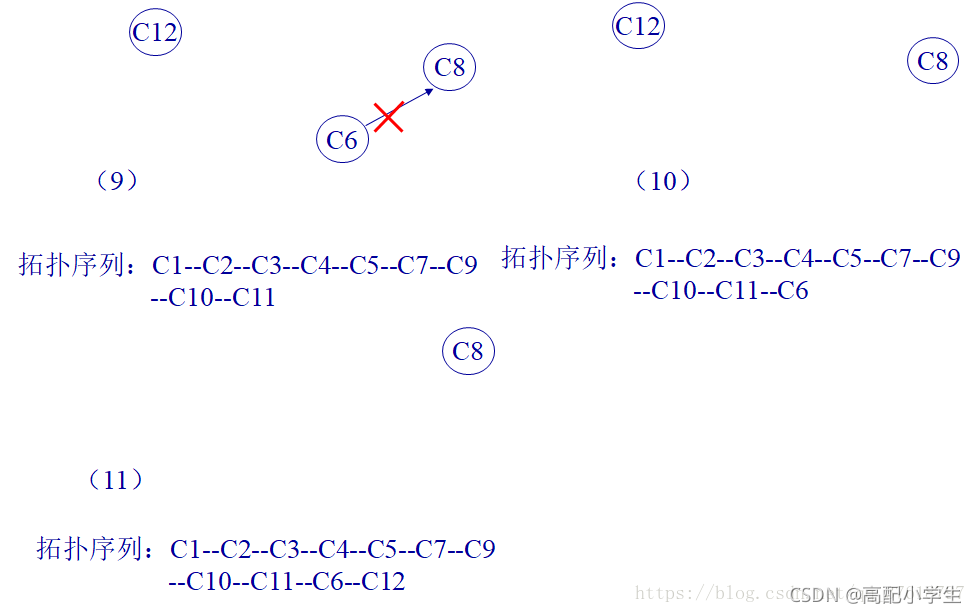
最终得拓扑序列:C1–C2–C3–C4–C5–C7–C9–C10–C11–C6–C12–C8。
注意:拓扑序列并不唯一,C9–C10–C11–C6–C1–C12–C4–C2–C3–C5–C7–C8 也是一种拓扑序列。
再偷个板子
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <string>
#include <functional>
#include <cstring>
#include <cctype>
#include <stack>
#include <queue>
#include <set>
#define IOS() std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
#define Max 505
using namespace std;
vector<int> vec[Max]; //vec 存图
priority_queue<int,vector<int>,greater<int> > q; //优先队列
int in_deg[Max];//入度
int ans[Max];
int n,m;
void init() {
for(int i=0; i<=n; i++) {
vec[i].clear();
}
memset(in_deg,0,sizeof(in_deg));
while(!q.empty()) q.pop();
}
bool topsort() {
for(int i=0; i<n; i++) {
if(in_deg[i]==0) {
q.push(i);
}
}
int cnt=0;
while(!q.empty()) {
int a=q.top();
q.pop();
ans[cnt++]=a;
for(int i=0; i<vec[a].size(); i++) {
in_deg[vec[a][i]]--;
if(in_deg[vec[a][i]]==0) {
q.push(vec[a][i]);
}
}
}
return cnt==n;
// if(cnt!=n) cout<<-1<<endl;
// else {
// for(int i=0; i<cnt-1; i++) {
// cout<<ans[i]<<" ";
// }
// cout<<ans[cnt-1]<<endl;
cout<<endl;
// }
}
int main() {
IOS();
while(cin>>n>>m) {
if(m==0&&n==0)break;
init();
for(int i=0; i<m; i++) {
int u,v;
cin>>u>>v;
vec[u].push_back(v);
in_deg[v]++;
}
if(topsort()) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
## 最后的最后
有些时候我们需要反向构造图,这些情况往往是对不唯一的排序结果唯一化的时候所需要做的