题目一

力扣:LCP44

在这里插入图片描述

思路

1、需要知道所有的火焰，所以就是遍历一遍二叉树
2、需要快速的直到当前火焰我是否统计过，所以用unordered_set，利用hash表。

代码：

class Solution {
public:
	unordered_set<int> item;//快速查找该点是否出现过
	int ans = 0;//个数
	void dfs(TreeNode* root) {//中根遍历
		if (root == nullptr) {
			return;
		}
		dfs(root->left);
		if (item.count(root->val) == 0) {//没出现过就统计一下，并且加入集合
			ans++;
			item.insert(root->val);
		}
		dfs(root->right);
	}
	int numColor(TreeNode* root) {
		dfs(root);
		return ans;
	}
};

（所有代码均已在力扣上运行无误）

经测试，该代码运行情况是(经过多次测试所得最短时间)：
在这里插入图片描述

题目二

力扣:LCP46
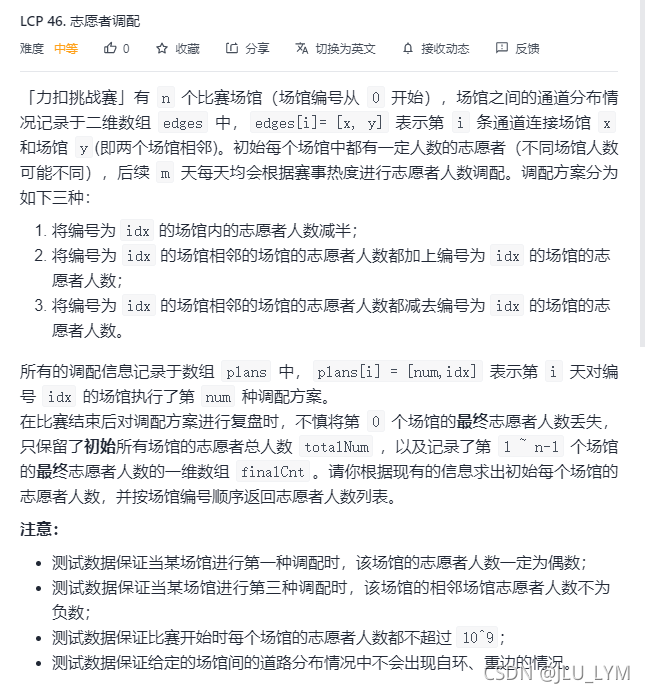
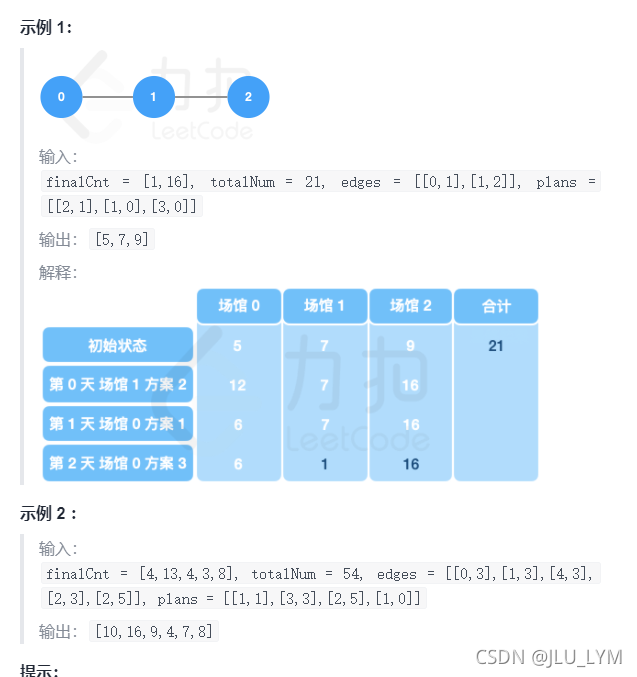
在这里插入图片描述

思路

1、很明显，这题是一个在无向图上讨论的问题，所以第一步就是存图，方法见我的博客力扣207，但这个题是无向图，我们这样想就行，无向图等于有两个方向，即(u,v)可从u到v,反之亦可，所以存储的时候正反存就行。
2、本题如果说0号场地有多少人是知道的，就不难了，但是目前就是不到，所以很简单列方程
3、在解方程和整理方程的时候，其实就是变化参数，所以常数位,x,x^2 …甚至别的未知量，这些不变，变得只是参数，所以几个未知量，就写几个存储参数的数组就行了，这就是计算机模拟解方程的过程，本体就是一元一次方程，所以用两个数组存参数就行了，剩下的数学咋计算参数，则这里就直接模拟即可。

代码

注意：！！！！！！！！！！！！！！！！！！！！！！！！
1、这题里面数据量贼大，所以尽可能少用int ，多使用long long
2、switch语句一定要写break;
3、做除法前要先验证分母是否为零！

class Solution {
public:
	vector<vector<int>> edge;//邻接表
	//涉及解方程，用数组存参数变化就得了
	vector<long long> k;//x的系数
	vector<long long> j;//常数
	vector<int> ans;//答案
	vector<int> volunteerDeployment(vector<int>& finalCnt, long long totalNum, vector<vector<int>>& edges, vector<vector<int>>& plans) {
		long long n = finalCnt.size();//范围少一
		long long  n1 = plans.size() - 1;


		edge.resize(n + 1);//范围大小读题
		for (long long  i = 0; i < edges.size(); i++) {
			vector<int> tmp = edges[i];
			edge[tmp[0]].push_back(tmp[1]);//无向图建图
			edge[tmp[1]].push_back(tmp[0]);
		}

		k.resize(n + 1);//x系数初始化，只有第一个未知
		k[0] = 1;
		for (int i = 1; i < n + 1; i++) {
			k[i] = 0;
		}

		j.resize(n + 1);//常数初始化，只有第一个未知
		j[0] = 0;
		for (int i = 0; i < n; i++) {
			j[i + 1] = finalCnt[i];
		}


		for (long long  i = n1; i >= 0; i--) {//因为要逆推，所以反向模拟
			long long point = plans[i][1];//目标点
			long long plan = plans[i][0];//调动计划
			switch (plan) {//以下计算其实就是两个系数分开算就行
			case 1:
				k[point] *= 2;
				j[point] *= 2;
				break;
			case 2:
				for (int e : edge[point]) {
					k[e] -= k[point];
					j[e] -= j[point];
				}
				break;
			case 3:
				for (int e : edge[point]) {
					k[e] += k[point];
					j[e] += j[point];
				}
				break;
			}
		}

		long long sum_j = 0, sum_k = 0;
		for (int i = 0; i < n + 1; i++) {
			sum_j += j[i];
			sum_k += k[i];
		}
		if (sum_k != 0) {//分母不为零，计算出x
			int x = (totalNum - sum_j) / sum_k;
			for (int i = 0; i < n + 1; i++) {
				ans.push_back(k[i] * x + j[i]);
			}
		}
		else {//分母为零，常数即为答案
			for (int i = 0; i < n + 1; i++) {
				ans.push_back(j[i]);
			}
		}
		return ans;
	}
};