高空抛物危害巨大,对人的生命财产安全造成重大威胁,本文就抛物问题简单建立数学模型,进行初步的计算分析。
假设抛出的物体初速度都是水平方向,受到地球重力加速度作用,且受到空气阻力作用,空气阻力大小跟物体速度大小平方成正比,跟速度方向相反。那么最终的公式为
? ? ?(1)
? (2)
下面用matlab进行建模分析,假设物体质量为1kg,空气阻力系数为c=0.05,重力加速度为g=9.8m/s^2,水平初速度为v0 = 1m/s。且有
,? ??
,? ? ? ??
我们计算十秒的时间,那么有如下matlab代码:
function main()
clc;clear
m = 1; % 1kg重物
c = 0.05; % 阻力系数
g = 9.8; %重力加速度
v0 = 1; %初始水平速度
H = 0; %初始高度
v02 = 0; %初始竖直速度
D = 0; %初始水平距离
[t,x] = ode45(@(t,x)odefun(t,x,m,c,g), [0,10], [D, v0, 0, v02]);
plot(x(:,3),x(:,1))
xlabel('抛物高度');
ylabel('落地距离')
title(['初速度',num2str(v0),'m/s',';风阻力系数:',num2str(c)])
end
function dxdt = odefun(t, x, m, c, g)
dxdt = zeros(4,1);%初始化
resist = -c*norm([x(2),x(4)])*[x(2),x(4)];
dxdt(1) = x(2);%水平方向位移对t导数
dxdt(2) = resist(1)/m;%水平方向速度对t导数
dxdt(3) = x(4);%竖直方向位移对t导数
dxdt(4) = (m*g + resist(2))/m;%竖直方向速度对t导数
end计算得到该条件下,水平最大飞行距离和垂直楼高之间的关系如下图
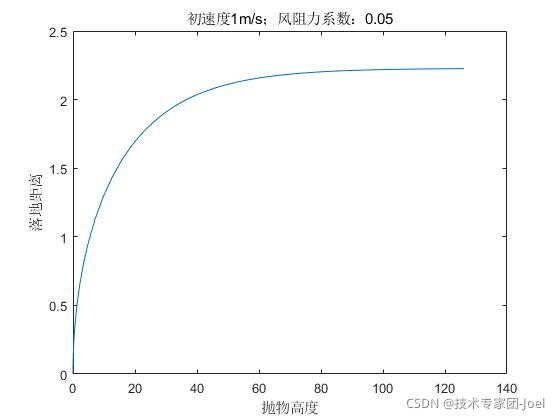
?可见,当楼层在40m以下的时候,抛物落地距离随着高度增大急剧增加,后来由于风阻力系数影响,抛物落地距离逐渐趋于一个水平,即2.22m。
该模型及程序可以为高层楼下设计花坛等隔断距离,为住户安全设计提供参考。