数学规划模型
一、概述
1.什么是数学规划?
运筹学的一个分支,用来研究在给定条件下(即约束条件),如何按照某一衡量指标(目标函数)来寻求计划、管理工作中的最优方案。
即求目标函数在一定约束条件下的极值问题
2.数学规划的一般形式
min(or max)Z=f(x)
s.t gi(x)<=0,i=1,2,…,m (不等式约束) 约束条件,也可能等式约束、整数约束…
x:决策变量(一般多个自变量)
f(x):目标函数

3.数学规划的分类
(1)线性规划
目标函数f(x)和约束条件均是决策变量的线性表达式。
(2)非线性规划
目标函数f(x)或者约束条件中有一个是决策变量x的非线性表达式。
此类问题没有通用算法,大多算法是在选定决策变量的初始值后,通过一定寻求最优的决策变量(3)整数规划
一类要求变量取整数值得数学规划,可分为线性整数规划(在线性规划模型中,有决策变量限定为整数)和非线性规划。
目前流行的求解整数规划的算法只适用于线性整数规划
(4)0-1规划:整数规划的特例,整数变量取值只能0和1
二、线性规划问题的求解
1.matlab中线性规划的标准型

举例:如何将下列线性规划问题转换为matlab中的标准型
(1)
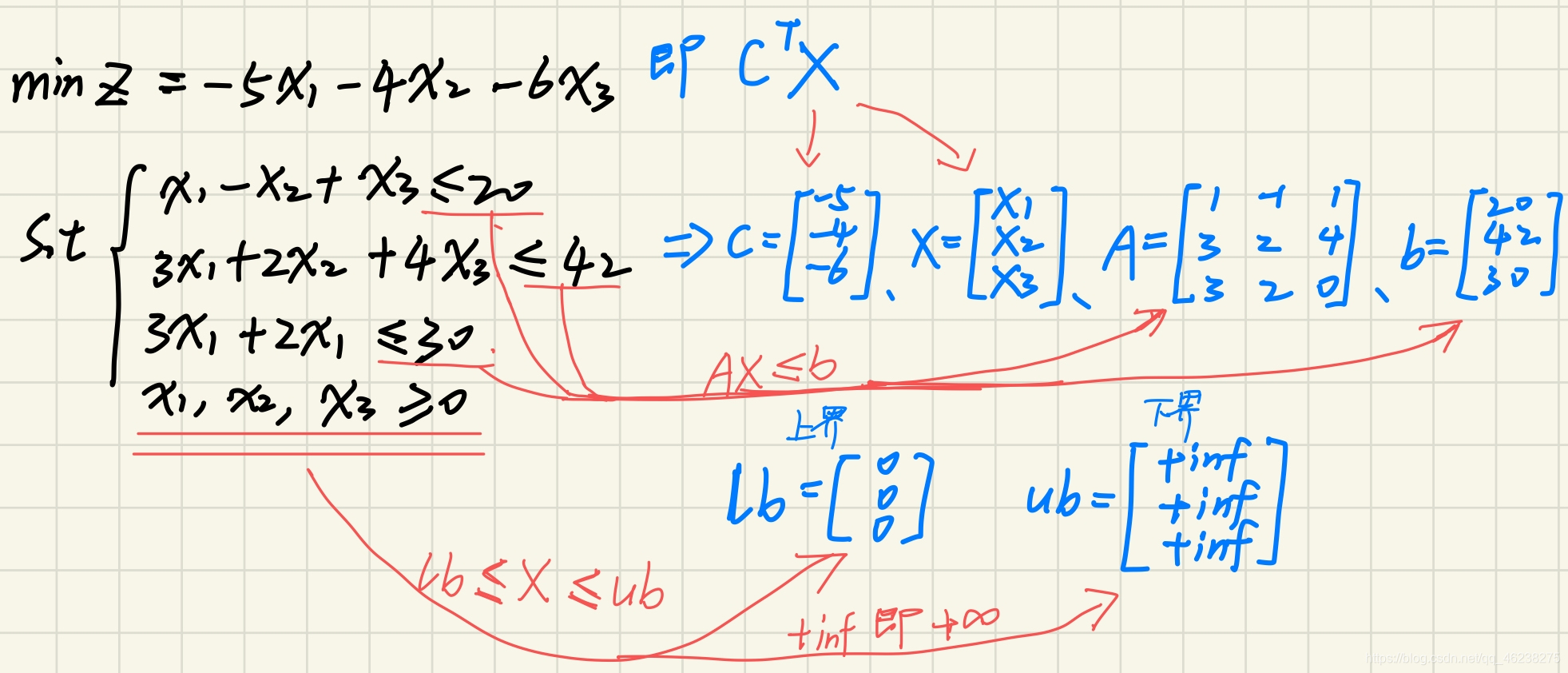
(2)

(3)

matlab求解线性规划的函数

例题1(生产决策问题)
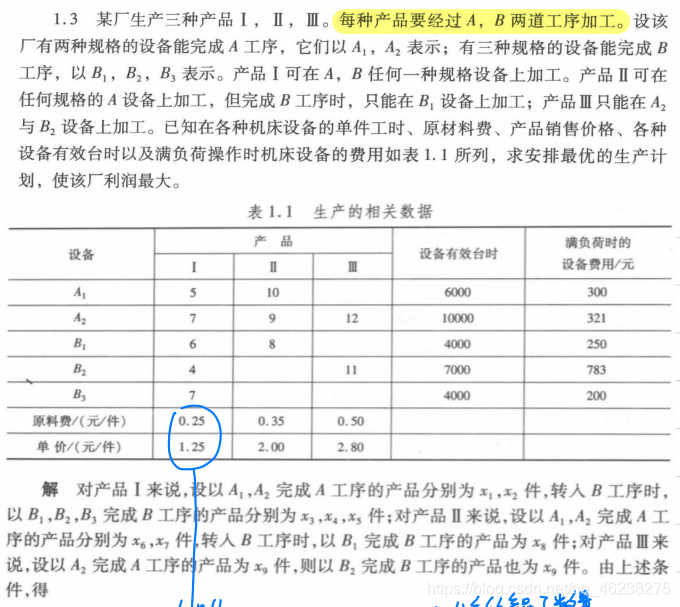

例题2(投料问题)
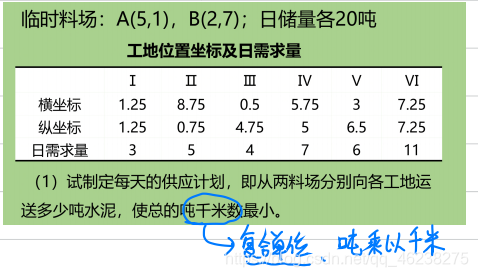
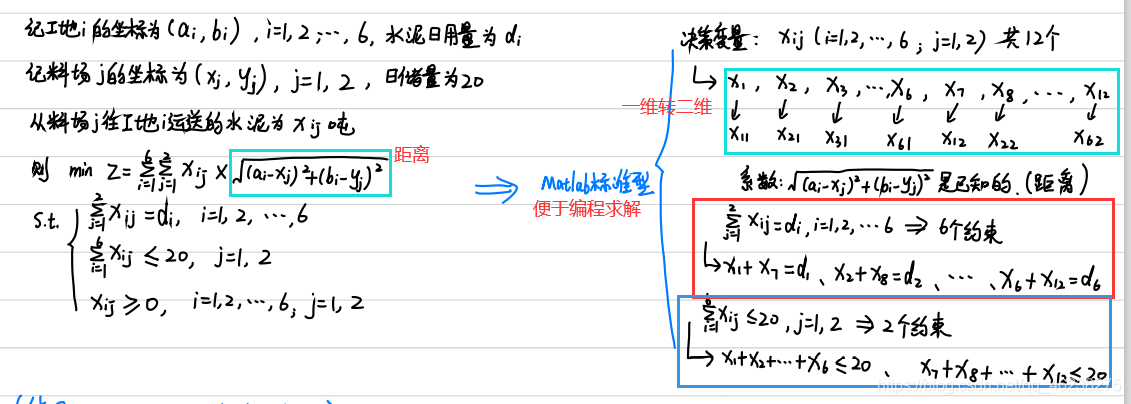
三、整数规划问题的求解
整数规划问题:
线性整数规划:matlab可进行求解(线性指的在线性规划的基础上,加入决策变量取整数的条件);
非线性整数规划:没有特定算法,只能用近似算法,如蒙特卡洛模拟、智能算法
特例:特殊的整数规划问题,0-1规划
matlab中也只能求解线性0-1规划,对于非线性0-1规划也只能近似求解(但比赛中常出现)


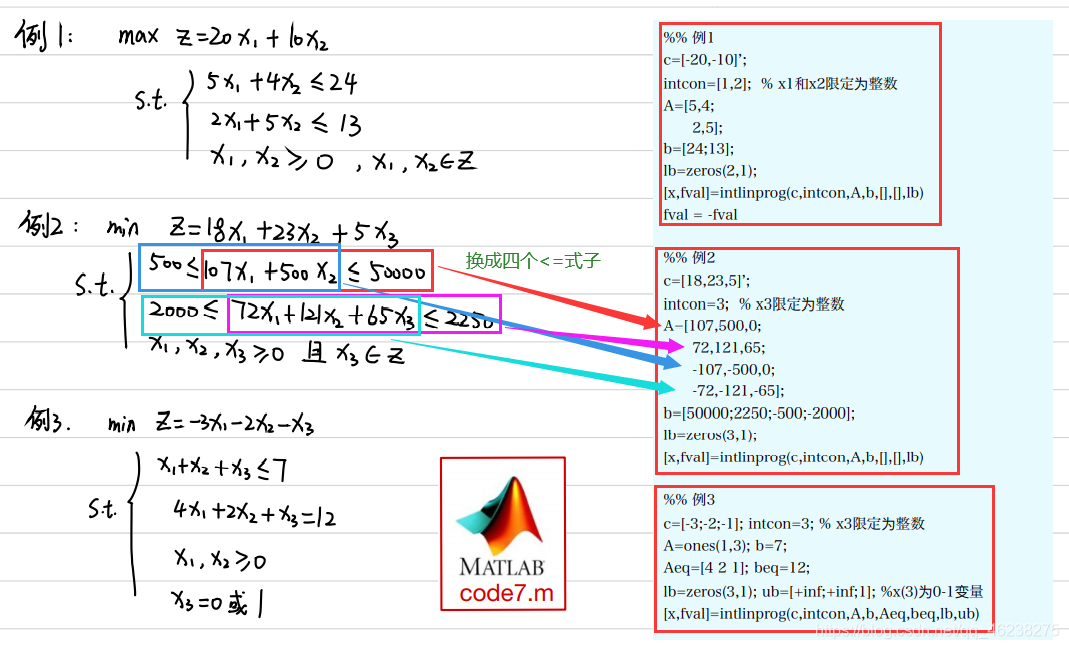
例题1(0-1背包问题)
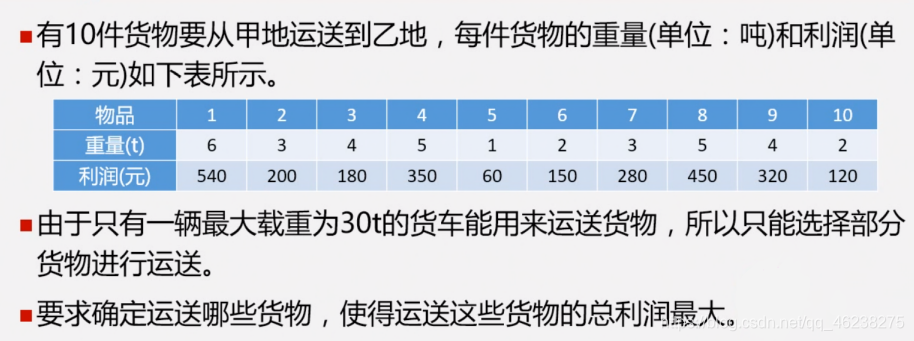

例题2(指派问题)
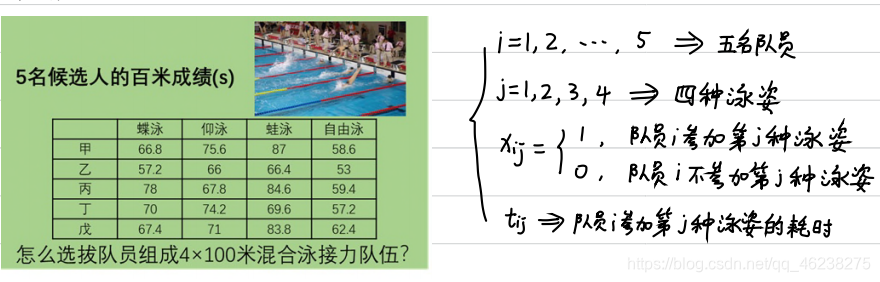

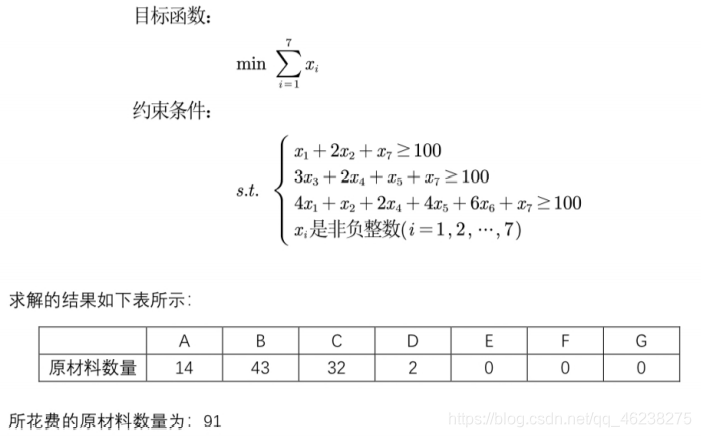
例题3(钢管切割问题)

四、非线性规划问题的求解

练习:将非线性规划问题转换为matlab中的标准型


解释:

