[数据结构与算法]力扣LeetCode

排序衍生

^运算符

^ 异或操作，理解为不进位相加
有交换率。
a^a=0
a^0=a

public static void sway(int[] arr,int i,int j){
	if(i!=j){
		//不能两个值指向同一地址
	    arr[i]=arr[i]^arr[j];
	    arr[j]=arr[i]^arr[j];//就是arr[i]^arr[j]^arr[j]就表示a
	    arr[i]=arr[i]^arr[j];//表示arr[i]^arr[j]^arr[i]^arr[j]^arr[j]就是b
    }
}

找一个单数

一组数只有一个数出现一次，其他出现两次，找出这个数：

    public static void main(String[] args) {
        int[] ints = {2, 2, 4, 4, 6, 8, 99, 99, 6, 8, 43, 76, 43, 76, 111};
        int med=0;
        for (int a:ints){
            med^=a;//两次出现就会变成0，单数就保留
        }
        System.out.println(med);
    }

找两个个单数

一组数只有两个数出现一次，其他出现两次，找出这两个数：

    public static void main(String[] args) {
        int[] ints = {2, 2, 4, 4, 6, 8, 99, 99, 6, 8, 43, 76, 43, 76, 111,333};
        int med=0;
        for (int a:ints){
            med^=a;//两个不同的单数^最后得到med
        }
        int rightOne=med&(~med+1);//取出med中二进制为1的位值（必存在，因为不同值）
        int med1=0;
        for (int a:ints){
            //对应位为1的值取出进行^最后的到两个单数对应位为1的
            // (a&rightOne)== 0得到对应位为0
            if ((a&rightOne)== rightOne){
                med1^=a;
            }
        }
        System.out.println(med1);//两个单数其中一个值
        System.out.println(med^med1);//两个单数令一个值
    }

基于归并排序的小数和

数组的每个值前比他本身小的和的总和。求数组的小数和

    public static int mergeSortTest(int[] arr, int left, int right, int[] temp){
        if(left<right){
            int m=(left+right)/2;
            return
            mergeSortTest(arr,left,m,temp)+
            mergeSortTest(arr,m+1,right,temp)+
            mergeTest(arr,left,m,right,temp);
        }
        return 0;
    }
    private static int mergeTest(int[] arr, int left, int m, int right, int[] temp) {
        int i=left;
        int j=m+1;
        int tempIndex=0;
        int res=0;
        while (i<=m&&j<=right){
            res+=arr[i]<arr[j]?arr[i]*(right-j+1):0;//若左小，就是会出现小数的位置。个数有右侧确定。
            temp[tempIndex++]=arr[i]<arr[j]?arr[i++]:arr[j++];
        }
        while (i<=m)
            temp[tempIndex++]=arr[i++];
        while (j<=right)
            temp[tempIndex++]=arr[j++];
        System.arraycopy(temp, 0, arr, left, tempIndex);
        return res;
    }

二分衍生

查找极小值

该值比左右的值都小，如果是在数组两侧则只比较一点即可。
在无序数组中找到该极小值

public class Test{
    public static void main(String[] args) {
        System.out.println(limitMin(new int[]{235, 34,53, 53, 354, 454, 45, 65}, 0, 7));
    }
    public static int limitMin(int[] arr,int left,int right){
        if(arr[left]<arr[left+1]){
            return arr[left];
        }else if (arr[right]<arr[right-1]){
            return arr[right];
        }
        int med=(left+right)/2;
        if(arr[med+1]>arr[med]){
            return limitMin(arr,left,med);
        }else {
            return limitMin(arr,med,right);
        }
    }
}

链表衍生

判断链表的回文

package Test;
import java.util.Stack;

public class Test {
    public static void main(String[] args) {
        LinkedList list = new LinkedList();
        list.add(1);
        list.add(5);
        list.add(3);
        list.add(7);
        list.add(3);
        list.add(5);
        list.add(1);
        LinkedList list1 = new LinkedList();
        list1.add(1);
        list1.add(4);
        list1.add(4);
        list1.add(1);
        System.out.println(IsTrue.isTrue_1(list.header));
        System.out.println(IsTrue.isTrue_2(list.header));
        System.out.println(IsTrue.isTrue_1(list1.header));
        System.out.println(IsTrue.isTrue_2(list1.header));
        System.out.println(IsTrue.isTrue_3(list1.header));
        System.out.println(IsTrue.isTrue_3(list.header));
    }
}
class IsTrue{
    public static boolean isTrue_1(Node header){
        if (header==null)throw new RuntimeException("空");
        Node tail=header;
        Stack<Node> stack = new Stack<>();
        while (tail!=null){
            stack.push(tail);
            tail=tail.next;
        }
        tail=header;
        while (tail!=null){
            if (tail.num!=stack.pop().num)
                return false;
            tail=tail.next;
        }
        return true;
    }
    public static boolean isTrue_2(Node header){
        if (header==null||header.next==null)return true;
        Node slow=header;
        Node quick=header;
        while (quick.next!=null&&quick.next.next!=null){
            slow=slow.next;
            quick=quick.next.next;
        }
        slow=slow.next;
        Stack<Node> nodes = new Stack<Node>();
        while (slow!=null){
            nodes.push(slow);
            slow=slow.next;
        }
        slow=header;
        while (!nodes.isEmpty()){
            if (slow.num!=nodes.pop().num)
                return false;
            slow=slow.next;
        }
        return true;
    }
    public static boolean isTrue_3(Node header) {
        if (header == null || header.next == null) return true;
        Node node1 = header;
        Node node2 = header;
        while (node2.next != null && node2.next.next != null) {
            node1 = node1.next;
            node2 = node2.next.next;
        }
        node2 = node1.next;
        node1.next = null;
        Node node3;
        //将后一半链表指向反向
        while (node2 != null) {
            node3 = node2.next;
            node2.next = node1;
            node1 = node2;
            node2 = node3;
        }
        node2 = header;
        node3 = node1;
        boolean flag = true;
        //从两头进行判断
        while (node2 != null&&node3!=null) {//node3!=null多余，因为node2链表节点必定不少于node3节点
            if (node3.num!=node2.num){
                flag=false;
                break;
            }
            node3 = node3.next;
            node2 = node2.next;
        }
        node3 = node1.next;
        node1.next = null;
        //将后面一半反向后再反过来（恢复）
        while (node3 != null) {
            node2 = node3.next;
            node3.next = node1;
            node1 = node3;
            node3 = node2;
        }
        return flag;
    }
}

//链表的类
class LinkedList{
    Node header;
    public void add(int num){
        if (header==null){
            header=new Node(num,null);
            return;
        }
        Node tail=header;
        while (tail.next!=null){
            tail=tail.next;
        }
        tail.next=new Node(num,null);
    }

}
class Node{
    int num;
    Node next;
    public Node(int num, Node next) {
        this.num = num;
        this.next = next;
    }
}

复制随机指向的链表

package Test;

public class Test {
    public static void main(String[] args) {
        Node header=new Node(0);
        Node node1=new Node(1);
        Node node2=new Node(2);
        Node node3=new Node(3);
        Node node4=new Node(4);
        Node node5=new Node(5);
        header.next=node1;
        node1.next=node2;
        node2.next=node3;
        node3.next=node4;
        node4.next= node5;
        node1.rand=node4;
        node3.rand=node2;
        node5.rand=node1;
        CopyLinkedList.copy_1(header);
        CopyLinkedList.copy_2(header);
    }
}
class CopyLinkedList{
    public static Node copy_1(Node header){
        if (header==null)return null;
        HashMap<Node, Node> map = new HashMap<Node, Node>();
        Node tail=header;
        while (tail!=null){
        //遍历填入哈希表
            map.put(tail,new Node(tail.value));
            tail=tail.next;
        }
        tail=header;
        while (tail!=null){
            map.get(tail).next=map.get(tail.next);
            map.get(tail).rand=map.get(tail.rand);
            tail=tail.next;
        }
        return map.get(header);
    }
    
    public static Node copy_2(Node header){
        if (header==null)return null;
        Node tail=header;
        Node n;
        //在原来节点后再添加一个copy节点
        while (tail!=null){
            n=tail.next;
            tail.next=new Node(tail.value);
            tail.next.next=n;
            tail=n;
        }
        tail=header;
        Node copyTail;
        //复制处理rand节点（只对原节点判断）
        while (tail!=null){
            n=tail.next.next;
            copyTail=tail.next;
            if (tail.rand!=null)
                copyTail.rand=tail.rand.next;
            tail=n;
        }
        Node copyHeader=header.next;//若不提前标记会被回收
        tail=header;
        //链表分离
        while (tail!=null){
            n=tail.next.next;
            copyTail=tail.next;
            if (n!=null)
                copyTail.next=n.next;
            tail.next=n;
            tail=n;
        }
        return copyHeader;
    }
}
class Node{
    int value;
    Node next;
    Node rand;
    public Node(int value){
        this.value=value;
    }
}

三分链表

给定一个只将比该值小的节点放左边，大的放右边

class SEL{
    public static Node sEL(Node header,int pivot){
        Node head_1=null;
        Node tail_1=null;
        Node head_2=null;
        Node tail_2=null;
        Node head_3=null;
        Node tail_3=null;
        Node nextNode=null;
        while (header!=null){
            nextNode=header.next;
            header.next=null;
            if (header.num<pivot){
                if (head_1==null){
                    head_1=header;
                    tail_1=header;
                }else {
                    tail_1.next=header;
                    tail_1=tail_1.next;
                }
            }else if (header.num==pivot){
                if (head_2==null){
                    head_2=header;
                    tail_2=header;
                }else {
                    tail_2.next=header;
                    tail_2=tail_2.next;
                }
            }else {
                if (head_3==null){
                    head_3=header;
                    tail_3=header;
                }else {
                    tail_3.next=header;
                    tail_3=tail_3.next;
                }
            }
            header=nextNode;
        }
        if (tail_1==null){
            if (tail_2==null){
                return head_3;
            }else {
                tail_2.next=head_3;
                return head_2;
            }
        }else {
            if (tail_2==null){
                tail_1.next=head_3;
            }else {
                tail_1.next=head_2;
                tail_2.next=head_3;
            }
            return head_1;
        }
    }
}

判断链表是否有环

判断链表是否有环，若有返回第一个入环节点
慢:1 快:2
若慢:1快3：
都入环时相差奇数步，且环节点数量为偶数则永不相交

都入环时相差奇数步说明每次差值减少2步，定在第一轮反超，此时差 环节点个数-1，若该值仍为奇数，那么第二轮也反超，故永不相遇

package Test;

public class Test {
    public static void main(String[] args) {
        Node header=new Node(0);
        Node node1=new Node(1);
        Node node2=new Node(2);
        Node node3=new Node(3);
        Node node4=new Node(4);
        Node node5=new Node(5);
        header.next=node1;
        node1.next=node2;
        node2.next=node3;
        node3.next=node4;
        node4.next=node5;
        node5.next=node2;
        System.out.println(HasCircle.hasCircle(header).num);

    }
}
class HasCircle{
    public static Node hasCircle(Node header){
        if (header==null)return null;
        boolean flag=false;
        Node slow=header;
        Node quick=header;
        while (quick.next!=null&&quick.next.next!=null){
            slow=slow.next;
            quick=quick.next.next;
            if (slow==quick){//判断是否却有环
                flag=true;
                break;
            }
        }
        if (!flag)return null;
        quick=header;
        while (quick!=slow){//相遇时将其中一个指针指向header走相同的步数定在入环节点相遇
            quick=quick.next;
            slow=slow.next;
        }
        return quick;
    }
}
class Node{
    int num;
    Node next;
    public Node(int num){
        this.num=num;
    }
}

两个链表相交关系

class List{
    /*
    有环：
            1.同环：
                - 入环节点相同  返回相交节点
                - 入环节点不同  返回其中一个入环节点
            2.不同环：
                - 返回null
     无环：
            1.相交：
                - 返回相交节点
            2.不相交：
                - 返回null
     */
    public static Node getIntersectNode(Node head1, Node head2) {
        if (head1 == null || head2 == null) {
            return null;
        }
        Node loop1 = hasCircle(head1);
        Node loop2 = hasCircle(head2);
        if (loop1 == null && loop2 == null) {
            return noLoop(head1, head2);//无环，判断是否为链式相交或不相交
        }
        if (loop1 != null && loop2 != null) {
            return bothLoop(head1, loop1, head2, loop2);//有环，返回相交节点
        }
        return null;//一有环，一无环必定不相交
    }


    private static Node hasCircle(Node header){
        if (header==null)return null;
        boolean flag=false;
        Node slow=header;
        Node quick=header;
        while (quick.next!=null&&quick.next.next!=null){
            slow=slow.next;
            quick=quick.next.next;
            if (slow==quick){//判断是否却有环
                flag=true;
                break;
            }
        }
        if (!flag)return null;
        quick=header;
        while (quick!=slow){//相遇时将其中一个指针指向header走相同的步数定在入环节点相遇
            quick=quick.next;
            slow=slow.next;
        }
        return quick;
    }

    private static Node noLoop(Node head1, Node head2) {
        if (head1 == null || head2 == null) {
            return null;
        }
        Node cur1 = head1;
        Node cur2 = head2;
        int n = 0;
        //计算链表差值
        while (cur1.next != null) {
            n++;
            cur1 = cur1.next;
        }
        while (cur2.next != null) {
            n--;
            cur2 = cur2.next;
        }
        if (cur1 != cur2) {
            return null;
        }
        cur1 = n > 0 ? head1 : head2;
        cur2 = cur1 == head1 ? head2 : head1;
        n = Math.abs(n);
        //长的走到和短的长度同位置
        while (n != 0) {
            n--;
            cur1 = cur1.next;
        }
        //判断是否有相同节点，若无就会走到最后返回null
        while (cur1 != cur2) {
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        return cur1;
    }

    private static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
        Node cur1 = null;
        Node cur2 = null;
        if (loop1 == loop2) {
            cur1 = head1;
            cur2 = head2;
            int n = 0;
            while (cur1 != loop1) {
                n++;
                cur1 = cur1.next;
            }
            while (cur2 != loop2) {
                n--;
                cur2 = cur2.next;
            }
            cur1 = n > 0 ? head1 : head2;
            cur2 = cur1 == head1 ? head2 : head1;
            n = Math.abs(n);
            while (n != 0) {
                n--;
                cur1 = cur1.next;
            }
            while (cur1 != cur2) {
                cur1 = cur1.next;
                cur2 = cur2.next;
            }
            return cur1;
        } else {
            cur1 = loop1.next;
            while (cur1 != loop1) {
                if (cur1 == loop2) {
                    return loop1;//环内相交
                }
                cur1 = cur1.next;
            }
            return null;//两个有环链表环不是同一个
        }
    }
}
class Node{
    int value;
    Node next;
    public Node(int num){
        this.value=num;
    }
}

优先队列

持续输出中位数（堆/优先队列）

持续输入一个数，可以在任意时刻输出中位数。

• 构建两个堆，一个大堆，一个小堆，大堆放较小的元素，小堆放较大的元素
• 持续保持两个堆的元素个数差不超过1
• 超过1，将大堆中堆顶元素放进小堆或将小堆堆顶元素放进大堆。
• 这样中位数就一直只和两个堆的堆顶元素相关

class Tree {
    private PriorityQueue<Double> little;//存较大数据,取出较小元素
    private PriorityQueue<Double> large;//存较小数据,取出较大元素

    public Tree() {
        little = new PriorityQueue<>();
        large = new PriorityQueue<>((o1, o2) -> Double.compare(o2, o1));
    }
    public void add(Double x) {
        if (little.size() == 0 && large.size() == 0)
            large.add(x);
        else {
            if (large.peek() < x)little.add(x);
            else large.add(x);
            if (little.size() - large.size() > 1)
                large.add(little.poll());
            else if (little.size() - large.size() < -1)
                little.add(large.poll());
        }
    }
    public Double getMed(){
        if (little.size()-large.size()==0)
            return (little.peek()+large.peek())/2;
        else if (little.size()-large.size()>0)
            return little.peek();
        else return large.peek();
    }
}

二叉树衍生

前中后横向遍历非递归实现

package Test;

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Stack;

public class Test {
    public static void main(String[] args) {
        Node root=new Node(0);
        Node node1=new Node(1);
        Node node2=new Node(2);
        Node node3=new Node(3);
        Node node4=new Node(4);
        Node node5=new Node(5);
        root.left=node1;
        root.right=node2;
        node1.left=node3;
        node1.right=node4;
        node4.right=node5;
        Tree.pre(root);
        System.out.println();
        Tree.inOrderUnRecur(root);
        System.out.println();
        Tree.posOrderUnRecur1(root);
        System.out.println();
        Tree.posOrderUnRecur2(root);

    }
}
class Tree{
    //前序遍历
    public static void pre(Node root){
        System.out.print("pre-order: ");
        if (root==null)return;
        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            Node n=stack.pop();
            System.out.print(n.value+" ");
            if (n.right!=null){
                stack.push(n.right);
            }
            if (n.left!=null){
                stack.push(n.left);
            }
        }
    }
    //中序遍历
    public static void inOrderUnRecur(Node head) {
        System.out.print("in-order: ");
        if (head != null) {
            Stack<Node> stack = new Stack<Node>();
            while (!stack.isEmpty() || head != null) {
                if (head != null) {//向左搜索压入栈中，向右不入栈
                    stack.push(head);
                    head = head.left;
                } else {//持续搜索右树
                    head = stack.pop();
                    System.out.print(head.value + " ");
                    head = head.right;
                }
            }
        }
        System.out.println();
    }

    //后序遍历
    public static void posOrderUnRecur1(Node head) {
        System.out.print("pos-order: ");
        if (head != null) {
            Stack<Node> s1 = new Stack<Node>();
            Stack<Node> s2 = new Stack<Node>();
            s1.push(head);
            while (!s1.isEmpty()) {
                head = s1.pop();
                s2.push(head);
                if (head.left != null) {
                    s1.push(head.left);
                }
                if (head.right != null) {
                    s1.push(head.right);
                }
            }
            while (!s2.isEmpty()) {
                System.out.print(s2.pop().value + " ");
            }
        }
        System.out.println();
    }

    //后序遍历
    public static void posOrderUnRecur2(Node h) {
        System.out.print("pos-order: ");
        if (h != null) {
            Stack<Node> stack = new Stack<Node>();
            stack.push(h);
            Node c = null;
            while (!stack.isEmpty()) {
                c = stack.peek();
                if (c.left != null && h != c.left && h != c.right) {
                    stack.push(c.left);
                } else if (c.right != null && h != c.right) {
                    stack.push(c.right);
                } else {
                    System.out.print(stack.pop().value + " ");
                    h = c;
                }
            }
        }
        System.out.println();
    }
    //横向遍历
    public static void w(Node root){
        if (root==null)return;
        Deque<Node> deque=new ArrayDeque();
        deque.add(root);
        while (!deque.isEmpty()){
            Node n=deque.poll();
            System.out.println(n);
            if (n.left!=null){
                deque.add(n.left);
            }
            if (n.right!=null){
                deque.add(n.right);
            }
        }
    }

}
class Node{
    int value;
    Node left;
    Node right;
    public Node(int num){
        this.value=num;
    }
}

计算树每一层的最多节点个数

class Tree{
    //基于横向遍历
    public static int fun_1(Node root) {
        if (root == null) return 0;
        Deque<Node> deque = new ArrayDeque();
        HashMap<Node, Integer> map = new HashMap<Node, Integer>();
        deque.add(root);
        int floor=1;//运行的这一层是哪一层
        int thisNum=0;//本层节点个数
        int maxNum = 0;//每一层最大的值
        map.put(root,floor);
        while (!deque.isEmpty()) {
            Node n = deque.poll();
            if (map.get(n)==floor){//如果还是这一层
                thisNum++;
            }else {//如果和上一层不一层了
                maxNum=Math.max(maxNum,thisNum);
                thisNum=1;//因为已经删除了该层一个元素，所以初始化为1
                floor++;//进行下一层
            }
            if (n.left != null) {
                deque.add(n.left);//进入队列
                map.put(n.left,floor+1);//记录该元素层数
            }
            if (n.right != null) {
                deque.add(n.right);
                map.put(n.right,floor+1);
            }
        }
        return Math.max(thisNum,maxNum);
    }

	//基于横向遍历
    public static int fun_2(Node root) {
        if (root == null) return 0;
        Node thisLastNode=root;//记录遍历节点层的最后一个节点
        Node nextLastNode=null;//记录遍历节点下一层最后一个结点
        int maxNum=0;
        int thisNum=0;//当前层节点个数
        Deque<Node> deque = new ArrayDeque();
        deque.add(root);
        while (!deque.isEmpty()) {
            Node n = deque.poll();
            thisNum++;//删除一个就加1
            if (n.left != null) {
                deque.add(n.left);
                nextLastNode=n.left;//更新最后一个节点
            }
            if (n.right != null) {
                deque.add(n.right);
                nextLastNode=n.right;//更新最后一个节点
            }
            if (n==thisLastNode){//删除的借点和该层节点相同说明该层结束
                thisLastNode=nextLastNode;//将下一层最后的节点给thisLastNode
                nextLastNode=null;//以后动态遍历下一层
                maxNum=Math.max(thisNum,maxNum);//记录最大值
                thisNum=0;
            }
        }
        return maxNum;
    }
}
class Node{
    int value;
    Node left;
    Node right;
    public Node(int num){
        this.value=num;
    }
}

判断是搜索二叉树（套路题）

isBST_2递归套路：

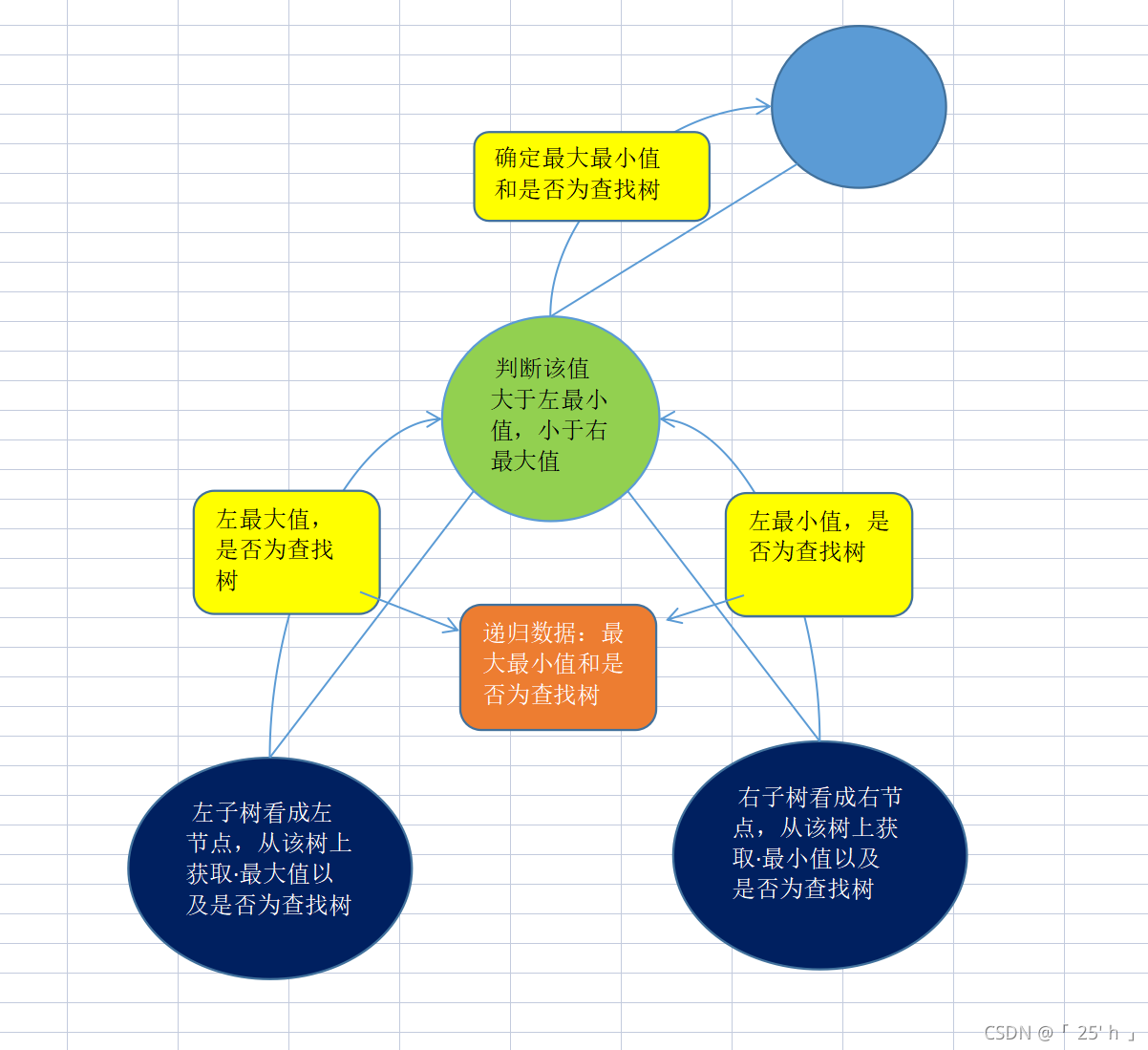
class Tree{
    //中序遍历判断
    private static int last=Integer.MIN_VALUE;
    public static boolean isBST_1(Node head){
        if (head==null){
            return true;
        }
        if (!isBST_1(head.left))return false;
        if (last>=head.value)return false;
        else last=head.value;
        return isBST_1(head.right);
    }
    
    
    //套路递归判断
    public static returnType isBST_2(Node head){
        if (head==null)return null;
        returnType leftType= isBST_2(head.left);
        returnType rightType= isBST_2(head.right);

        int min=head.value;//初始值
        int max=head.value;
        boolean flag=true;

        //左判断刷新
        if (leftType!=null){
            if (!leftType.isbst||leftType.max>=head.value)flag=false;
            min=Math.min(leftType.min,head.value);
            max=Math.max(leftType.max,head.value);
        }
        //右判断刷新
        if (rightType!=null){
            if (!rightType.isbst||rightType.min<=head.value)flag=false;
            min=Math.min(rightType.min,head.value);
            max=Math.max(rightType.max,head.value);
        }
        return new returnType(min,max,flag);
    }
    static class returnType{
        boolean isbst;
        int min;
        int max;
        private returnType(int min, int max, boolean flag){
            this.min=min;
            this.max=max;
            this.isbst=flag;
        }
    }
}
class Node{
    int value;
    Node left;
    Node right;
    public Node(int num){
        this.value=num;
    }
}

判断是完全二叉树（套路题）

class Tree {
    public static boolean isCBT(Node head) {
        if (head == null) return true;
        boolean flag = false;
        Deque<Node> deque = new ArrayDeque<Node>();
        deque.add(head);
        while (!deque.isEmpty()) {
            Node node = deque.pop();
            if ((node.left == null && node.right != null)//左无节点有有节点
                    ||
                    (flag && (node.right != null || node.right != null)))//标记后左右存在节点
                return false;
            if (node.left != null) deque.add(node.left);
            if (node.right != null) deque.add(node.right);
            if (node.left == null || node.right == null) flag = true;//此后不该有子节点，应该放在最后判断，因为判断结果flag不能对此次结果有影响
        }
        return true;
    }
}

class Node {
    int value;
    Node left;
    Node right;

    public Node(int num) {
        this.value = num;
    }
}

判断是满二叉树（套路题）

递归套路：

class Tree {
	//方式一
    public static boolean isF_1(Node head){
        Data data = is_1(head);
        return (1<<data.height)-1==data.nodeNum;
    }
    private static Data is_1(Node head){
        if (head==null)return new Data(0,0);
        Data lData=is_1(head.left);
        Data rData=is_1(head.right);
        int num=lData.nodeNum+rData.nodeNum+1;
        int he=Math.max(lData.height,rData.height)+1;
        return new Data(num,he);
    }


	//方式二
    public static boolean isF_2(Node head){
        Data data = is_2(head);
        return data != null;
    }
    private static Data is_2(Node head){
        if (head==null)return new Data(0,0);
        Data lData=is_2(head.left);
        Data rData=is_2(head.right);
        if (lData==null||rData==null)
            return null;
        if (lData.nodeNum!=rData.nodeNum||lData.height!=rData.height)
            return null;
        int num=lData.nodeNum+rData.nodeNum+1;
        int he=lData.height+1;
        return new Data(num,he);
    }

    static class Data{
        int nodeNum;
        int height;
        boolean is;
        public Data(int nodeNum,int height){
            this.nodeNum=nodeNum;
            this.height=height;
        }
    }
}

class Node {
    int value;
    Node left;
    Node right;
    public Node(int num) {
        this.value = num;
    }
}

判断是平衡树（套路题）

递归套路：

class Tree {
    public static Data isAVL(Node head){
        if (head==null)return new Data(0,true);
        Data lData=isAVL(head.left);
        Data rData=isAVL(head.right);
        int height=Math.max(lData.height,rData.height)+1;
        boolean flag=lData.isAVL&&rData.isAVL&&Math.abs(lData.height-rData.height)<=1;
        return new Data(height,flag);
    }

    static class Data{
        int height;
        boolean isAVL;
        public Data(int height ,boolean is){
            this.height=height;
            this.isAVL=is;
        }
    }
}

class Node {
    int value;
    Node left;
    Node right;
    public Node(int num) {
        this.value = num;
    }
}

树节点最远距离（套路题）

递归套路：

• 根据子树最大深度计算出经过当前节点的最长距离
• 向上传递子树和经过当前节点最长距离 的最大值
• 最长距离需要子树深度
• 所以递归数据包括最大距离和最大深度

class U {
    public static Data maxLength(Node head){
        if (head==null)return new Data(0,0);
        Data ld=maxLength(head.left);
        Data rd=maxLength(head.right);
        int maxLen=Math.max(ld.maxHeight+rd.maxHeight+1,Math.max(ld.maxLen,ld.maxLen));
        int maxHeight=Math.max(ld.maxHeight,rd.maxHeight)+1;
        return new Data(maxLen,maxHeight);
    }
    private static class Data{
        int maxLen;
        int maxHeight;
        private Data(int maxLen,int maxHeight){
            this.maxLen=maxLen;
            this.maxHeight=maxHeight;
        }
    }
}

最大快乐值（套路题）

递归套路：

• 最大值和每个节点是否去有关，就是取 当前节点不去（0）+子节点去或不去的最大值 和 当前节点去（happy）+子节点不去的最大值
• 每个节点的去和不去都会直接影响父类节点，间接影响祖宗节点。
• 只要递归传递该节点去和不去的最大值信息即可。

class U {
    public static Data maxHappy(Node head){
        if (head.nexts==null)return new Data(0,head.happy);
        int lai=head.happy;
        int bu=0;
        for (Node node:head.nexts){
            Data data = maxHappy(node);
            lai+=data.maxBu;//该节点去，子节点不能去
            bu+=Math.max(data.maxBu,data.maxLai);//该节点不去，子节点可取可不去
        }
        return new Data(bu,lai);
    }
    private static class Data{
        int maxBu;
        int maxLai;
        private Data(int maxBu,int maxLai){
            this.maxBu =maxBu;
            this.maxLai =maxLai;
        }
    }
}
class Node {
    int happy;
    Node[] nexts;
}

查找树中两个节点的最近共父类节点

• 该路径上不存在寻找的o1或o2，就回馈上一次递归null
• 路径上存在o1或o2，返回标记告诉上一次递归存在o1或o2
• 直到在某次递归时判断出左右路径都回馈了有o1或o2，就将该父节点返回
• 将返回的父节点以返回值的方式传给上一次递归直至结束递归。

class Tree {
    /**
     * @param header   根节点
     * @param o1    节点一
     * @param o2    节点二
     * @return  最近共父节点
     * 
     */
    public static Node ancestor(Node header, Node o1, Node o2) {
        if (header == null || o1 == header || o2 == header) return header;
        Node lNode = ancestor(header.left, o1, o2);
        Node rNode = ancestor(header.right, o1, o2);
        
        //该条件只会成功一次，返回的header就是我们所要找的节点
        // 如何将这个节点返回第一次调用这个函数时？
        //      由于我们不知道这个父节点是它的父节点的左还是右
        //      但是我们知道成功进入该条件后的所有递归中只能出现一边为null，另一边为header节点
        //      所以 返回： lNode != null ? lNode : rNode
        //          另外这句话也会在找到目标节点前将o1或o2传到上一个递归中，代表着这个路径上存在o1或o2
        //          当路径上没有o1或o2时，lNode和rNode均为空，随便返回一个
        if (lNode != null && rNode != null)
            return header;
        return lNode != null ? lNode : rNode;
    }
}
class Node {
    int value;
    Node left;
    Node right;
    public Node(int num) {
        this.value = num;
    }
}

查找后继结点

• 有右节点，右树上的最左节点
• 无右节点，递归寻找节点是父节点左节点的点
• 否则空

class Tree {
    public static Node process(Node node){
        if (node==null)return null;
        if (node.right!=null)return leftLast(node.right);//有右节点
        Node parentTail=node.parent;
        while (parentTail!=null&&parentTail.left!=node){//递归寻找节点
            node=parentTail;
            parentTail=parentTail.parent;
        }
        return parentTail;
    }
    private static Node leftLast(Node head){//一直寻找左节点
        while (head.left!=null)
            head=head.left;
        return head;
    }
}

class Node {
    int value;
    Node left;
    Node right;
    Node parent;
    public Node(int num) {
        this.value = num;
    }
}

折纸凹凸问题

上次每个折痕都有两个子折痕，上凹下凸，也就是二叉树节点都有一个凹左节点一个凸右节点。这些折痕的顺序就是二叉树的中序遍历。

class Tree {
    /**
     * @param N 折N次
     */
    public static void pre(int N){
        pre(N,true);
    }
    private static void pre(int num,boolean down){
        if (num==0)return;
        pre(num-1,true);//true表示凹，false表示凸
        System.out.print(down?"down ":"up ");
        pre(num-1,false);
    }
}

哈夫曼最小代价问题

class Tree {
    public static int lessConsumer(int[] arr){
        if (arr.length==1)return arr[0];
        PriorityQueue<Integer> queue = new PriorityQueue<>();//内部元素为堆结构（优先队列）
        for (int i : arr)
            queue.add(i);
        int sum=0;
        while (queue.size()>1){
            //构建赫夫曼树
            int num1=queue.poll();
            int num2=queue.poll();
            sum+=(num1+num2);
            queue.add(num1+num2);
        }
        return sum;
    }
}

暴力递归

N皇后（位运算）

class E {
    public static int num(int num) {
        if (num < 1 || num > 32) return 0;
        //limit用于限制在所有数据运算过程中保证除后num位的所有位数据均为零，来判断结束和标志结束
        int limit = num == 32 ? -1 : (1 << num) - 1;
        return process(limit, 0, 0, 0);
    }

    /**
     * @param limit    限制数据在一定的位运算范围内
     * @param coLim    该步前所有皇后纵向上已经存在皇后
     * @param leftLim  该步前所有皇后在k=-1的方向上对于我们该步皇后存在的限制
     * @param rightLim 该步前所有皇后在k=1的方向上对于我们该步皇后存在的限制
     * @return 该路径上存在的的情况，只会在成功时返回1
     * coLim/leftLim/rightLim三者的限制均是在位上为1的时候表示存在皇后
     */
    private static int process(int limit, int coLim, int leftLim, int rightLim) {
        if (limit == coLim) return 1;

        //(coLim | leftLim | rightLim)结果表示所有位上为1的位置均存在皇后，不能存放。
        //~后表示1的地方没有限制，可以存放皇后（但是，在32位的前32-num位上也为1，我们知道这是不合理的，因为不存在那么多的皇后）
        //limit&    表示将除num位的值变成0，这样就保证所有为1的元素均为空缺位置。
        int pos = limit & (~(coLim | leftLim | rightLim));
        int res = 0, mostRightOne;
        while (pos != 0) {//pos为0.说明不存在空缺位置
            mostRightOne = pos & (~pos + 1);//此时在后num位存在1，就将最右端的1取出。
            pos = pos - mostRightOne;//更新pos，将取出的1减掉，表明mostRightOne中1所对应的位存在了，不能放了。
            res += process(limit, coLim | mostRightOne  // 该mostRightOne位的皇后对于下一皇后纵向上的影响
                    , (leftLim | mostRightOne) << 1     // mostRightOne对于k=-1方向的影响
                    , (rightLim | mostRightOne) >> 1);  //mostRightOne对于k=1方向的影响
        }
        return res;
    }
}

字符串的全排列

• 我们通常都思路都是将所有字符依次放在最前面，例如ABC，第一位为A，B,C，然后判断第二位，那么我们如何在字符串中标记该字符已经被我们安排在前面了？
• 若我们使用下标的方式，那么在每次选择都会产生一个下标，这样会很乱。
• 于是我们可以通过将欲放在前面的字符就直接放在前面（将字符一次和后面的交换），用一个下标指引我们前面已经定了多少的元素。
• 但是若我们交换后在后续调用时，数据顺序已经打乱，我们可能会造成重复情况，所以我们在每次运行后再将数据交换变成原来位置。
• 但是当数据有重复字符时，会出现重复的全排列，这是我们就要判断交换的字符是否和之前交换的相同，若相同，就不用交换

class PB {
    public static List<String> list=new ArrayList<>();
    public static void process(String string){
        char[] chars = string.toCharArray();
        process(chars,0);
    }
    private static void process(char[] chars, int i){
        if (i==chars.length){//结果
            list.add(new String(chars));
            return;
        }
        boolean[] isVisited=new boolean[26];//默认只有大写字母
        for (int j=i;j<chars.length;j++){
            if (!isVisited[chars[j]-'A']){//是否重复
                isVisited[chars[j]-'A']=true;
                swap(chars,i,j);//交换
                process(chars,i+1);//递归
                swap(chars,i,j);//恢复
            }
        }
    }
    private static void swap(char[] chars,int i, int j) {
        char c = chars[i];
        chars[i]=chars[j];
        chars[j]=c;
    }
}

纸牌累计分数

class PB {
    public static int win(int[] arr){
        if (arr.length==0)return 0;
        return Math.max(front(arr,0,arr.length-1), end(arr,0,arr.length-1));
    }
    //先手的人对应的数据
    private static int front(int[] arr,int left,int right){
        if (left==right)return arr[left];//先手的人，最后还剩一个数据就是这个人的
        //取那个值和下一次该我选的时候我的收益最大。
        return Math.max(arr[left]+end(arr,left+1,right),arr[right]+end(arr,left,right-1));
    }
    private static int end(int[] arr, int left, int right){
        if (left==right)return 0;
        return Math.min(front(arr,left+1,right),+front(arr,left,right-1));
    }
}

岛数量问题

class PB {
    private static int[][] arr;
    private static int N;
    private static int M;
    public static int process(int[][] arr){
        PB.arr=arr;
        PB.N=arr.length;
        PB.M=arr[0].length;
        int res=0;//记录结果
        for (int i=0;i<N;i++){
            for (int j=0;j<M;j++){
                if (arr[i][j]==1){//有1且为被感染
                    res++;
                    infect(i,j);//感染
                }
            }
        }
        return res;
    }
    // 感染函数
    private static void infect(int i, int j) {
        if (i<0||i>=N||j<0||j>=M||arr[i][j]!=1)return;
        arr[i][j]=2;
        infect(i-1,j);
        infect(i+1,j);
        infect(i,j-1);
        infect(i,j+1);
    }
}

返回字符串的所有子字符串（树形）

• 将该问题看成二分类问题，将所有的单个字符元素是否存在看成一个事件，通过对所有的单个字符判读存在情况就可以得出所有子字符串
• 这样可以理解为二叉树的情况，每一层的每个节点下有两个子节点，表示该层对应的字符是否添加进路径中，最后树的所有叶子节点对应的字符串就是所以子字符串
• 我们采用动态生成树的递归方法对树进行动态的遍历。（该树必定为满树）

class PB {
    public static List<String> list=new ArrayList<>();
    private static String s;
    public static void childrenString(String string){
        s=string;
        childrenString("",0);
    }
    
    private static void childrenString(String chlidString,int i){
        if (i==s.length()){//叶子节点
            list.add(chlidString);
            return;
        }
        childrenString(chlidString+s.charAt(i),i+1);//要这个字符
        childrenString(chlidString,i+1);//不要这个字符
    }
}

数字转化成字母（树形）

class PB {
    public static int process(String s,int i){
        //若一个不剩或这还剩一个，就返回1（保证剩的不为0），若此时不返回，说明还剩至少两个字符
        if (s.length()==i||(s.length()==i+1&&s.charAt(i)!='0'))return 1;
        if (s.charAt(i)=='0')return 0;//没有0开头匹配的元素
        int res=process(s,i+1);//一个字符的
        if (Integer.parseInt(s.substring(i,i+2))<=26)
            res+=process(s,i+2);//若满足匹配条件，进行两个字符的
        return res;//累加的结果返回就行了
    }
}

背包问题（树形）

• 和返回字符串的所有子字符串相似，判断每个物品是否装进了袋子两种选择
• 只需要用递归像树一样遍历所有选择取出最大值即可
• 这样的题可以使用动态规划O(N2),递归O(2^N),关于递归转为动态规划，后续再说。

class PB {
    private static int maxBag;
    private static int[] weights;
    private static int[] values;
    public static int process(int[] weights,int[] values,int maxBag){
        PB.maxBag=maxBag;
        PB.weights=weights;
        PB.values=values;
        return process(0,0,0);
    }

    /**
     * @param w 此时的权重
     * @param v 此时价值
     * @param i 当前已经判断到那个物品了
     * @return  最大价值
     */
    private static int process(int w,int v,int i){
        if (w>maxBag)return 0;
        if (i==weights.length)return v;
        return Math.max(process(w+weights[i],v+values[i],i+1),
                        process(w,v,i+1));
    }
}

贪心算法

最多场会议问题

• 按照结束时间安排

class Progrem {
    Time[] times;
    public Progrem(Time[] times, int timePoint){
        this.times=times;
        arrange(timePoint);
    }

    private void arrange(int timePoint) {
        Arrays.sort(times, Comparator.comparingInt(o -> o.end));
        int res=0;
        for (Time time : times) {
            if (time.start >= timePoint) {//下一个会议开始时间在上一个会议结束后。
                res++;//会议数量
                timePoint = time.end;//记录该会议结束时间。
            }
        }
        System.out.println(res);
    }

    static class Time{
        int start;
        int end;
        public Time(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }
}

投资收益问题

• 两个优先队列
• 一个按count的小根堆P1，另一个按profit的大根堆P2
• 在P1中找能投资的放在P2中，投资P2堆顶元素
• 循环遍历

class Program {
    public static int res(int[] counts,int[] profits,int k,int m){
        //按照count建堆
        PriorityQueue<Node> minCount = new PriorityQueue<>(Comparator.comparingInt(o -> o.count));
        //按照profit建堆
        PriorityQueue<Node> maxProfit = new PriorityQueue<>((o1, o2) -> Integer.compare(o2.profit,o1.profit));
        //初始化
        for (int i=0;i<counts.length;i++)
            minCount.add(new Node(counts[i],profits[i]));
        for (int i = 0; i < k; i++) {
            //能承担的放在maxProfit中
            while (!minCount.isEmpty()&&minCount.peek().count<m)
                maxProfit.add(minCount.poll());
            //太穷了，结束
            if (maxProfit.isEmpty()) return m;
            //投资profit最大的累加
            m+=maxProfit.poll().profit;
        }
        return m;
    }
    private static class Node{
        int count;
        int profit;
        private Node(int count,int profit){
            this.count=count;
            this.profit=profit;
        }
    }
}