[数据结构与算法]P2532 [AHOI2012]树屋阶梯 （卡特兰数状态转移方程写法）

P2532 [AHOI2012]树屋阶梯

分析：

• 考虑以阶梯左下角那个点为第一个钢材的左下角，那么第一个钢材摆放情况便如下图（以 $n=5$ 为例）

• 对每种情况分别讨论，那么问题都被分成了两个子问题，设f[n]表示摆放高度为n的台阶的方法数，那么：

$$f[5]=f[4]?f[0]+f[3]?f[1]+f[2]?f[2]+f[1]?f[3]+f[0]?f[4]=\sum _{x+y=5}f[x]?f[y](f[0]=f[1]=1)$$

? 显然，这就是卡特兰数了

• 但是这题很烦，还要用高精乘，本人懒得打了，结果在题解里翻到一个神奇的卡特兰数的状态转移方程：

$$f[i][j]=f[i?1][j]+f[i][j?1]$$

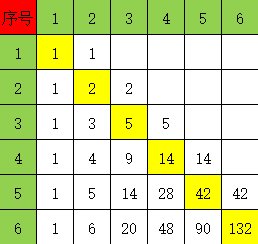
打表的代码：

#include <bits/stdc++.h>
using namespace std;

const int N=1005;
int f[N][N];
signed main()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    f[1][1]=f[1][2]=1;
    for(int i=2;i<=100;i++)
    {
        for(int j=1;j<=i+1;j++) f[i][j]=f[i-1][j]+f[i][j-1];
        // 这里的 f[i][i+1] 是为了保证下一行 f[i+1][i+1]的正确性 
    }
    for(int i=1;i<=10;i++)
    {
        for(int j=1;j<=i;j++)
        {
            printf("%-5d",f[i][j]);
        }printf("\n");
    }

    return 0;
}

还可以压缩为一维的，本身就是不断迭代的过程
$$f[i]=f[i]+f[i?1]$$

#include <bits/stdc++.h>
using namespace std;

int f[1005];
signed main()
{
    f[1]=1;
    for(int i=1;i<=10;i++)
    {
        for(int j=1;j<=i+1;j++)
        {
            f[j]=f[j-1]+f[j];
            if(j==i+1) { printf("\n"); continue; }
            printf("%-5d",f[j]);
        }
    }
    return 0;
}

最后再加上高精加就是本题的代码，$f[n][n]$ 第二维表示答案的位数

#include <bits/stdc++.h>
using namespace std;

const int N=1005;
int f[N][N];
signed main()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n;
    cin>>n;
    f[1][1]=1;
    int len=1;
    for(int i=2;i<=n+1;i++)
    {
        for(int j=1;j<=i;j++)
        {
            for(int k=1;k<=len;k++)
            {
                f[j][k]+=f[j-1][k];
            }
            for(int k=1;k<=len;k++)
            {
                f[j][k+1]+=f[j][k]/10;
                f[j][k]%=10;
            }
            while(f[j][len+1]) len++;
        }
    }
    for(int i=len;i>=1;i--) cout<<f[n][i];

    return 0;
}