剑指Offer（专项突破版）：栈

面试题36：后缀表达式

题目：后缀表达式是一种算术表达式，它的操作符在操作数的后面。输入一个用字符串数组表示的后缀表达式，请输出该后缀表达式的计算结果。假设输入的一定是有效的后缀表达式。例如，后缀表达式[“2”，“1”，“3”，""，"+"]对应的算术表达式是“2+13”，因此输出它的计算结果5。

面试题37：小行星碰撞

题目：输入一个表示小行星的数组，数组中每个数字的绝对值表示小行星的大小，数字的正负号表示小行星运动的方向，正号表示向右飞行，负号表示向左飞行。如果两颗小行星相撞，那么体积较小的小行星将会爆炸最终消失，体积较大的小行星不受影响。如果相撞的两颗小行星大小相同，那么它们都会爆炸消失。飞行方向相同的小行星永远不会相撞。求最终剩下的小行星。例如，有6颗小行星[4，5，-6，4，8，-5]，如图6.2所示（箭头表示飞行的方向），它们相撞之后最终剩下3颗小行星[-6，4，8]。

图6.2 用数组[4，5，-6，4，8，-5]表示的6颗小行星

面试题38：每日温度

题目：输入一个数组，它的每个数字是某天的温度。请计算每天需要等几天才会出现更高的温度。例如，如果输入数组[35，31，33，36，34]，那么输出为[3，1，1，0，0]。由于第1天的温度是35℃，要等3天才会出现更高的温度36℃，因此对应的输出为3。第4天的温度是36℃，后面没有更高的温度，它对应的输出是0。其他的以此类推。

面试题39：直方图最大矩形面积

题目：直方图是由排列在同一基线上的相邻柱子组成的图形。输入一个由非负数组成的数组，数组中的数字是直方图中柱子的高。求直方图中最大矩形面积。假设直方图中柱子的宽都为1。例如，输入数组[3，2，5，4，6，1，4，2]，其对应的直方图如图6.3所示，该直方图中最大矩形面积为12，如阴影部分所示。

图6.3 柱子高度分别为[3，2，5，4，6，1，4，2]的直方图

面试题40：矩阵中的最大矩形

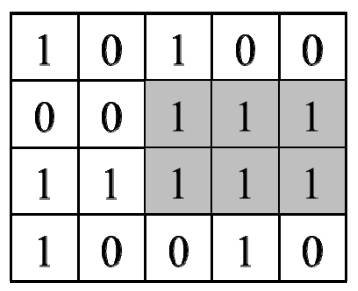
题目：请在一个由0、1组成的矩阵中找出最大的只包含1的矩形并输出它的面积。例如，在图6.6的矩阵中，最大的只包含1的矩阵如阴影部分所示，它的面积是6。

图6.6 一个由0、1组成的矩阵

划线笔记

栈是一种常用的数据结构，它最大的特点是 “后入先出”，即后进入栈中的元素最先出来。为了确保“后入先出” 的顺序，栈的插入和删除操作都发生在栈顶。

最大的特点是 “后入先出”，即后进入栈中的元素最先出来。为了确保“后入先出” 的顺序，栈的插入和删除操作都发生在栈顶。

Java 的库中提供了实现栈的类型 Stack。

函数 pop 和 peek 都能返回位于栈顶的元素，但函数 pop 会将位于栈顶的元素出栈，而函数 peek 不会。Stack 的函数 push、pop 和 peek 的时间复杂度都是_O_（1）。

如果数据保存的顺序和使用顺序相反，那么最后保存的数据最先被使用，具有 “后入先出” 的特点，所以可以考虑将数据保存到栈中。

很多时候保存在栈中的数据是排序的。根据题目的不同，栈中的数据既可能是递增排序的，也可能是递减排序的。因此，有人将这种用排序的栈解决问题的方法称为单调栈法。

后缀表达式又叫逆波兰式（Reverse Polish Notation，RPN），是一种将操作符放在操作数后面的算术表达式。通常用的是中缀表达式，即操作符位于两个操作数的中间，如 “2+1*3”。使用后缀表达式的好处是不需要使用括号。

后缀表达式不使用括号也能无歧义地表达这两个不同的算术表达式。

能提出有针对性的问题是学习能力的重要体现，在面试过程中这是一个加分项。

第 1 颗是向右飞行的大小为 4 的小行星。此时还不知道它会不会和其他小行星碰撞，可以先将它保存到某个数据容器中。第 2 颗还是一颗向右飞行的小行星，它的大小为 5。它和前面一颗小行星的飞行方向相同，所以不会碰撞。但现在还不知道它会不会和后面的小行星碰撞，因此也将它保存到数据容器中。第 3 颗是一颗向左飞行的小行星，大小为 6。由于它和前面两颗小行星是相向而行的，因此会和前面两颗小行星相撞。由于大小为 5 的小行星离它更近，因此这两颗小行星将会先相撞。先后向数据容器中保存了大小为 4、5 的两颗小行星，后保存到数据容器中的小行星先和其他的小行星相撞。这符合“后入先出” 的顺序，所以可以考虑用栈实现这个数据容器。

总结出小行星相撞的规律。如果一颗小行星向右飞行，那么可以将它入栈。如果一颗小行星是向左飞行的，而位于栈顶的小行星向右飞行，那么它将与位于栈顶的小行星相撞。如果位于栈顶的小行星较小，那么它将爆炸消失，也就是说它将出栈。然后判断它是否将与下一颗位于栈顶的小行星相撞。如果小行星与栈中所有小行星相撞之后仍然没有爆炸消失，那么将它入栈。

备注：
stack.stream().mapToInt(i->i).toArray()

栈中保存的小行星彼此都不会相撞。如果栈中既有向左飞行的小行星也有向右飞行的小行星，那么所有向左飞行的小行星都位于向右飞行的小行星的左边，也就是说，栈中的所有负数都位于正数的左边。因此，栈中的数值是部分排序的。

解决这个问题的直观方法很多人很快就能想到。对于数组中的每个温度，可以扫描它后面的温度直到发现一个更高的温度为止。如果数组包含_n_天的温度，那么这种思路的时间复杂度是_O_（_n_2）。

每次从数组中读出某一天的温度，并且都将其与之前的温度（也就是已经保存在数据容器中的温度）相比较。从离它较近的温度开始比较看起来是一个不错的选择，也就是后存入数据容器中的温度先拿出来比较，这契合 “后入先出” 的特性，所以可以考虑用栈实现这个数据容器。同时，需要计算出现更高温度的等待天数，存入栈中的数据应该是温度在数组中的下标。等待的天数就是两个温度在数组中的下标之差。

最终留在栈中的两天的后面都没有出现更高的温度。

解决这个问题的思路总结起来就是用一个栈保存每天的温度在数组中的下标。每次从数组中读取一个温度，然后将其与栈中保存的温度（根据下标可以得到温度）进行比较。如果当前温度比位于栈顶的温度高，那么就能知道位于栈顶那一天需要等待几天才会出现更高的温度。然后出栈 1 次，将当前温度与下一个位于栈顶的温度进行比较。如果栈中已经没有比当前温度低的温度，则将当前温度在数组中的下标入栈。

保存在栈中的温度（通过数组的下标可以得到温度）是递减排序的。这是因为如果当前温度比位于栈顶的温度高，位于栈顶的温度将出栈，所以每次入栈时当前温度一定比位于栈顶的温度低或相同。

仔细观察图 6.3 的直方图可以发现，这个直方图中最矮的柱子在数组中的下标是 5，它的高度是 1。这个直方图的最大矩形有 3 种可能。第 1 种是矩形通过这根最矮的柱子。通过最矮的柱子的最大矩形的高为 1，宽是 7。第 2 种是矩形的起始柱子和终止柱子都在最矮的柱子的左侧，也就是从下标为 0 的柱子到下标为 4 的柱子的直方图的最大矩形。第 3 种是矩形的起始柱子和终止柱子都在最矮的柱子的右侧，也就是从下标为 6 的柱子到下标为 7 的柱子的直方图的最大矩形。第 2 种和第 3 种从本质上来说和求整个直方图的最大矩形面积是同一个问题，可以调用递归函数解决。

计算通过该最矮的柱子的最大矩形面积并用变量 area 保存，然后递归求得最矮的柱子左右两侧子直方图的最大矩形面积并分别用变量 left 和 right 保存。这三者的最大值就是整个直方图最大矩形面积。

一种非常高效、巧妙的解法。这种解法用一个栈保存直方图的柱子，并且栈中的柱子的高度是递增排序的。为了方便计算矩形的宽度，栈中保存的是柱子在数组中的下标，可以根据下标得到柱子的高度。

这种解法的基本思想是确保保存在栈中的直方图的柱子的高度是递增排序的。假设从左到右逐一扫描数组中的每根柱子。如果当前柱子的高度大于位于栈顶的柱子的高度，那么将该柱子的下标入栈；否则，将位于栈顶的柱子的下标出栈，并且计算以位于栈顶的柱子为顶的最大矩形面积。

以某根柱子为顶的最大矩形，一定是从该柱子向两侧延伸直到遇到比它矮的柱子，这个最大矩形的高是该柱子的高，最大矩形的宽是两侧比它矮的柱子中间的间隔。

如果当前扫描到的柱子的高小于位于栈顶的柱子的高，那么将位于栈顶的柱子的下标出栈，并且计算以位于栈顶的柱子为顶的最大矩形面积。由于保存在栈中的柱子的高度是递增排序的，因此栈中位于栈顶前面的一根柱子一定比位于栈顶的柱子矮，于是很容易就能找到位于栈顶的柱子两侧比它矮的柱子。

此时栈中位于下标为 1 的柱子的左侧没有柱子。由于栈中的柱子的高度是递增排序的，如果下标为 1 的柱子的左侧存在较矮的柱子，那么较矮的柱子应该保存在栈中。现在栈中它的左侧没有柱子，这意味着它的左侧的柱子都比它高。因此，可以想象在下标为 - 1 的位置有一根比它矮的柱子。

当扫描数组中所有柱子之后，栈中可能仍然剩余一些柱子。因此，需要逐一将这些柱子的下标出栈并计算以它们为顶的最大矩形面积。

如果一根柱子的右侧有比它矮的柱子，那么当扫描到右侧较矮柱子的时候它就已经出栈了。因此，可以想象成以下标为 7 的柱子为顶的最大矩形往右一直延伸到下标为 8 的位置（8 为数组中柱子的数量，柱子的最大下标加 1）。栈中位于下标为 7 的柱子的左侧是下标为 5 的柱子，它的高为 1，比下标为 7 的柱子矮。

下标为 7 的柱子出栈之后位于栈顶的是下标为 5 的柱子，它的高为 1。栈中没有位于这根柱子左侧的柱子，这意味着它左侧的柱子都比它高。可以想象在下标为 - 1 的位置有一根比它矮的柱子。该柱子直到这个时候才出栈，说明它的右侧没有比它矮的柱子，可以想象成以下标为 5 的柱子为顶的最大矩形向右一直延伸到下标为 8 的位置。

假设输入数组的长度为_n_。直方图的每根柱子都入栈、出栈一次，并且在每根柱子的下标出栈时计算以它为顶的最大矩形面积，这些操作对每根柱子而言时间复杂度是_O_（1），因此这种单调栈法的时间复杂度是_O_（n）。这种解法需要一个辅助栈，栈中可能有_O_（n）根柱子在数组中的下标，因此空间复杂度是_O_（n）。