[数据结构与算法]LeetCode 1022. 从根到叶的二进制数之和

截止到目前我已经写了 600多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

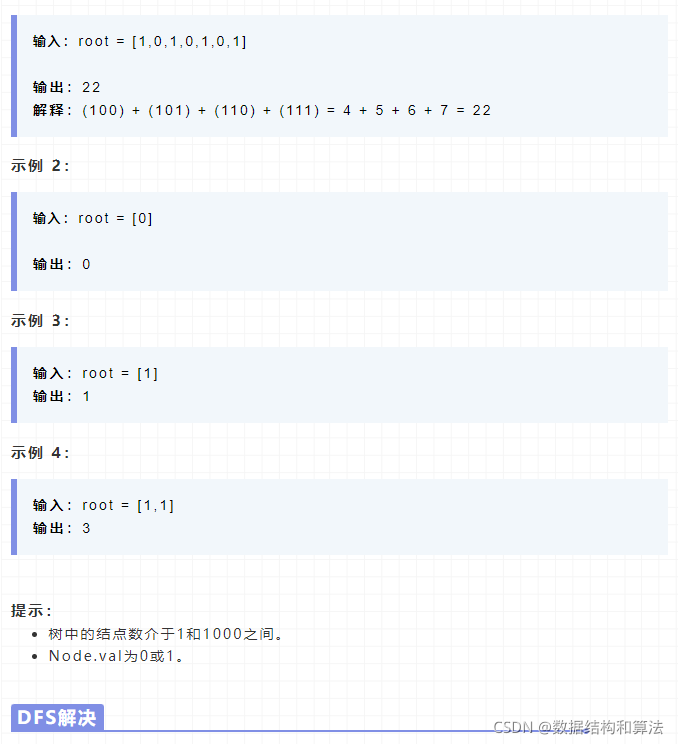
这里我们先画个图来看一下

我们可以看到从根节点到当前节点这条路径的值就是父节点的值*2加上当前节点的值。我们定义一个全局的变量res，他就是所有从根节点到叶子节点表示数字的和。

我们可以通过前序遍历来解这道题，当遇到叶子节点的时候就把从根节点到当前叶子节点表示的数字加到res中。直接把二叉树的前序遍历方式修改一下即可。

//最终返回的数字
int res = 0;

public int sumRootToLeaf(TreeNode root) {
    dfs(root, 0);
    return res;
}

//parentPathSum表示从根节点到当前父节点这条路径表示的数字
public void dfs(TreeNode root, int parentPathSum) {
    //如果节点为空，直接返回
    if (root == null)
        return;
    //父节点的值*2，在加上当前节点的值就是从根节点到
    //当前节点这条路径表示的数字
    int sum = parentPathSum * 2 + root.val;
    //如果到叶子节点，说明找到了一个从根节点到叶子
    //节点的完整路径，把这条路径的值加到res中
    if (root.left == null && root.right == null) {
        res += sum;
        return;
    }
    //如果没到叶子节点就继续遍历当前节点的左子节点和右子节点
    dfs(root.left, sum);
    dfs(root.right, sum);
}

时间复杂度：O(N)，N是节点的个数，所有节点都要访问一遍
空间复杂度：O(H)，H是树的最大高度，也是栈的深度

BFS解决
除了DFS，我们还可以使用BFS来解决，DFS就是深度优先搜索，BFS就是广度优先搜索，具体也可以看下373，数据结构-6,树。BFS就是一层一层的访问。这里需要使用两个队列：

• 一个存放节点
• 一个存放从根节点到当前节点这条路径表示的数字

如果访问到叶子节点的时候就把表示的数字加入到res中，最后返回res即可，我们来看下代码。

public int sumRootToLeaf(TreeNode root) {
    int res = 0;//结果值
    //两个队列，一个存放节点，一个存放从根节点到当前
    //节点的父节点这条路径所表示的数字
    Queue<TreeNode> queueNode = new LinkedList<>();
    Queue<Integer> queueParentSum = new LinkedList<>();
    queueNode.add(root);
    queueParentSum.add(0);
    while (!queueNode.isEmpty()) {
        TreeNode cur = queueNode.poll();
        int parentSum = queueParentSum.poll();
        //计算从根节点到当前节点这条路径表示的数字
        int sum = parentSum * 2 + cur.val;
        //如果当前节点是叶子节点，就把sum加到res中
        if (cur.left == null && cur.right == null) {
            res += sum;
            continue;
        }
        //如果左子节点不为空，就把他和他对应的值分别加入
        //到对应的队列中
        if (cur.left != null) {
            queueNode.add(cur.left);
            queueParentSum.add(sum);
        }
        //右子节点同上
        if (cur.right != null) {
            queueNode.add(cur.right);
            queueParentSum.add(sum);
        }
    }
    return res;
}

时间复杂度：O(N)，N是节点的个数，所有节点都要访问一遍。
空间复杂度：O(N)，这里使用了两个队列，因为队列中元素不停的进和出，最差情况下是满二叉树，到叶子节点的时候每个队列使用的空间是整颗树节点的一半(N/2)