[数据结构与算法]AcWing 674.超级2048

题目链接：674. 超级2048 - AcWing题库

2048?是一个著名的单人游戏，其目标是在网格上滑动图块以组合它们并创建数字为 2048?的图块。

2048?在一个简单的 4×4?网格上进行游戏，其中有一些图块，玩家可以对它们进行移动。

每一步操作，玩家可以选择向左，向右，向上和向下?4?个方向去移动所有图块。

如果两个包含数字相同的图块在移动时发生碰撞，则它们将合并为一个图块，该图块上的数值为两个图块的数字之和。

在一次操作中，一个新创建的图块不能再次参与合并，并且图块们总是优先沿着移动方向与其旁边的图块进行合并。

例如，如果三个?2?在一行构成?2 2 2，这时玩家选择向左移动，则它将变为?4 2 0，最左边的两个?22?会被合并。

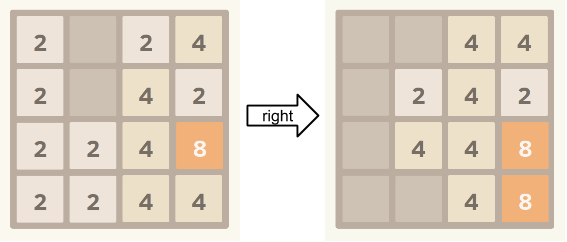
上图显示了当玩家将所有图块“右移”时4×4?网格的变化情况。

爱丽丝和鲍勃非常喜爱这个游戏。

但是几轮后，他们觉得网格的尺寸太小了并不刺激，所以决定将网格的尺寸扩大到?N×NN×N，他们称之为“超级 2048”游戏。

但是难度的激增让他们无法驾驭这个游戏。

他们要求你编写一个程序来帮助他们弄清楚在所有图块沿着某个特定方向移动后网格的样子。

输入格式

第一行包含整数?T，表示共有?T?组测试数据。

每组数据第一行包含整数?N?和一个字符串DIR，其中?N?表示网格的尺寸，DIR?表示图块的移动方向，DIR?将会是以下四个字符串中的一个：left,?right,?up,?down。

接下来?N?行，每行包含?N?个整数，用来描述网格的初始状态，每个整数表示网格中一个图块的值，如果为?00?则表示该位置是空的。

输出格式

对于每组测试数据，第一行输出?Case #x:，其中?xx?为组别编号（从?1?开始）。

然后输出?N?行，每行?N?个空格隔开的整数，表示图块移动后网格的样子。

数据范围

1≤T≤100
1≤N≤20
网格中的每个数字都是?0?或?2?到?1024?之间的?2?的整数次幂，包括?2?和 1024。

输入样例：

3
4 right
2 0 2 4
2 0 4 2
2 2 4 8
2 2 4 4
10 up
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
3 right
2 2 2
4 4 4
8 8 8

输出样例：

Case #1:
0 0 4 4
0 2 4 2
0 4 4 8
0 0 4 8
Case #2:
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
Case #3:
0 2 4
0 4 8
0 8 16

代码打卡：

#include <bits/stdc++.h>
using namespace std;

const int N = 30;
int arr[N][N];

void getUp(int n);
void getDown(int n);
void getLeft(int n);
void getRight(int n);

int main() {
    int t;cin >> t;
    for (int t1 = 1;t1 <= t;t1 ++) {
        int n;string str;
        cin >> n >> str;
        
        for (int i = 0;i < n;i ++) 
            for (int j = 0;j < n;j ++) cin >> arr[i][j];
        
        if (str == "up") getUp(n);
        if (str == "down") getDown(n);
        if (str == "left") getLeft(n);
        if (str == "right") getRight(n);
        
        cout << "Case #" << t1 << ":" << endl;
        for (int i = 0;i < n;i ++) {
            for (int j = 0;j < n;j ++) cout << arr[i][j] << ' ';
            cout << endl;
        }
    }
    return 0;
}

void getUp(int n){
    for (int i = 0;i < n;i ++) { // 遍历每一列
        int idx = 0;
        
        for (int j = 0;j < n;j ++) {
            if (arr[j][i] == 0) continue; // j => 行号
            
            if (j + 1 >= n) {
                arr[idx ++][i] = arr[j][i];
                continue;
            }
            
            int k = j + 1;
            
            while (k < n && arr[k][i] == 0) k ++;
            
            if (arr[j][i] == arr[k][i]) {
                arr[idx ++][i] = 2 * arr[j][i];
                j = k;
            }
            else arr[idx ++][i] = arr[j][i];
        }
        
        for (int j = idx;j < n;j ++) arr[j][i] = 0;
    }
}

void getDown(int n){
    for (int i = 0;i < n;i ++) { // 遍历每一列
        int idx = n - 1;
        
        for (int j = n - 1;j >= 0;j --) {
            if (arr[j][i] == 0) continue; // j => 行号
            
            if (j - 1 < 0) {
                arr[idx --][i] = arr[j][i];
                continue;
            }
            
            int k = j - 1;
            
            while (k >= 0 && arr[k][i] == 0) k --;
            
            if (arr[j][i] == arr[k][i]) {
                arr[idx --][i] = 2 * arr[j][i];
                j = k;
            }
            else arr[idx --][i] = arr[j][i];
        }
        
        for (int j = idx;j >= 0;j --) arr[j][i] = 0;
    }
}

void getLeft(int n){
    for (int i = 0;i < n;i ++) {
        int idx = 0;
        for (int j = 0;j < n;j ++) {
            if (arr[i][j] == 0) continue;
            
            if (j + 1 >= n) {
                arr[i][idx ++] = arr[i][j];
                continue;
            }
            
            int k = j + 1;
            
            while (k < n && arr[i][k] == 0) k ++;
            
            if (arr[i][j] == arr[i][k]) {
                arr[i][idx ++] = 2 * arr[i][k];
                j = k;
            }
            else arr[i][idx ++] = arr[i][j];
        }
        
        for (int j = idx;j < n;j ++) arr[i][j] = 0;
    }
}

void getRight(int n){
    for (int i = 0;i < n;i ++) {
        int idx = n - 1;
        for (int j = idx;j >= 0;j --) {
            if (arr[i][j] == 0) continue;
            
            if (j - 1 < 0) {
                arr[i][idx --] = arr[i][j];
                continue;
            }
            
            int k = j - 1;
            
            while (k >= 0 && arr[i][k] == 0) k --;
            
            if (arr[i][j] == arr[i][k]) {
                arr[i][idx --] = 2 * arr[i][k];
                j = k;
            }
            else arr[i][idx --] = arr[i][j];
        }
        
        for (int j = idx;j >= 0;j --) arr[i][j] = 0;
    }
}