T1 19. 正则表达式匹配
| 转移方程dp[i][j] | 条件 |
|---|---|
| dp[i][j-2] dp[i-1][j] & s[i-1] = p[j-2] dp[i-1][j] & p[j-2] = ‘.’ | p[j-1]=’*’ |
| dp[i-1][j-1] & s[i-1] = p[j-1] dp[i-1][j-1] & p[j-1] =’.’ | p[j-1] ≠ ‘*’ |
public boolean isMatch(String s, String p) {
int m = s.length() + 1, n = p.length() + 1;
boolean[][] dp = new boolean[m][n];
dp[0][0] = true; //此时都为空,可以匹配
for(int j = 2; j < n; j += 2)
//当s为空时,p必须满足a*b*.*这样的结构才能匹配成空串
//当s不为空,p为空为false
dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
//判断p的第j位是不是*,是*则判断前一位与i是否相等,相等则可以匹配0次或者多次
if(p.charAt(j-1) == '*'){
//此时i和j的前一位可以直接匹配,若匹配0次,j还要向前看一位j-2看是否匹配,如a和aa*匹配
//若匹配多次,j不变,i向前看一位,若i-1位匹配0次,则说明i匹配一次,若
//i-1匹配1次,则i匹配两次,所以j的位置保持不动,缩小i向前匹配即可,如 aaa和a*
//j-1是*时j不可能在首位,j-2不会越界
if(s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.'){
dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
}else{
//若前一位不能匹配只能匹配0次,j再向前看一位能否匹配,如aab和aaba*
//可以和上面的情况整合一下
dp[i][j] = dp[i][j-2];
}
}else{//不是'*',则只需要看上一位i和上一位j是否匹配,如aab和aa.
dp[i][j] = dp[i - 1][j - 1] && (p.charAt(j - 1) == '.' || s.charAt(i - 1) == p.charAt(j - 1));
}
}
}
return dp[m - 1][n - 1];
}
T2 49. 丑数
1,2,3,5
2的倍数、3的倍数、5的倍数
6的倍数,10的倍数,15的倍数,30的倍数
丑数递推 丑数 = 小丑数 × 某因子
x
n
+
1
=
m
i
n
(
x
a
×
2
,
x
b
?
×
,
x
c
×
5
)
x_n+_1 = min(x_a×2,x_b*×,x_c×5)
xn?+1?=min(xa?×2,xb??×,xc?×5)
动态规划
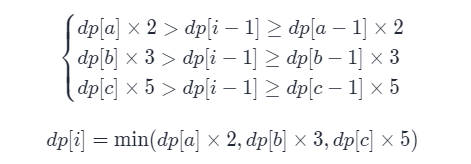
class Solution {
public int nthUglyNumber(int n) {
int a=0,b=0,c=0; //a:含因子2; b含因子3; c含因子5
int[] dp= new int[n]; //n个丑数
dp[0]=1; //1是第1个丑数
for(int i=1;i<n;i++){
int n2 = dp[a]*2,n3=dp[b]*3,n5=dp[c]*5;
dp[i] = Math.min(Math.min(n2,n3),n5); //丑数 = 较小小丑数 × 某因子
if(dp[i]==n2) a++;
if(dp[i]==n3) b++;
if(dp[i]==n5) c++;
//使用if是当有多个匹配因子要同时引动下标如 6要引动a,b
}
return dp[n-1];
}
}
T3 60. n个骰子的点数
6n点数组合

class Solution {
public double[] dicesProbability(int n) {
double[] dp = new double[6]; //1个骰子
Arrays.fill(dp,1.0/6.0); //初始化1/6
for(int i=2;i<=n;i++){ //2个骰子开始
double[] tmp = new double[5*i+1]; //n个骰子的最大值 6n
for(int j=0;j<dp.length;j++){
for(int k=0;k<6;k++){
tmp[j+k] += dp[j] /6.0; //正向解决越界问题
}
}
dp = tmp;
}
return dp;
}
}