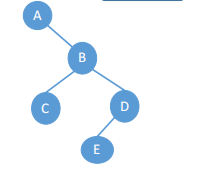
一、一种遍历确定二叉树?
通过先、中、后序遍历的序列,确定唯一的二叉树。
例如:BDCAE的的中序遍历:中序遍历左子树、根结点、中序遍历右子树。可以画出不同的树。
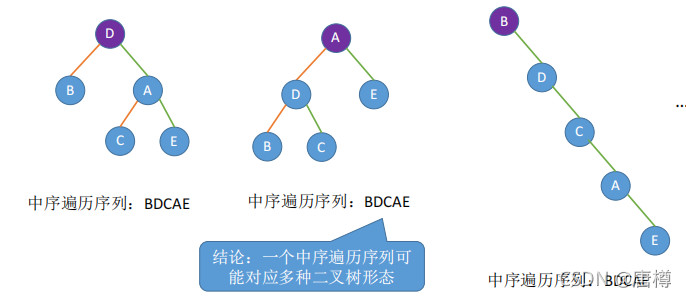
BDCAE的前序遍历,画出不同的树。
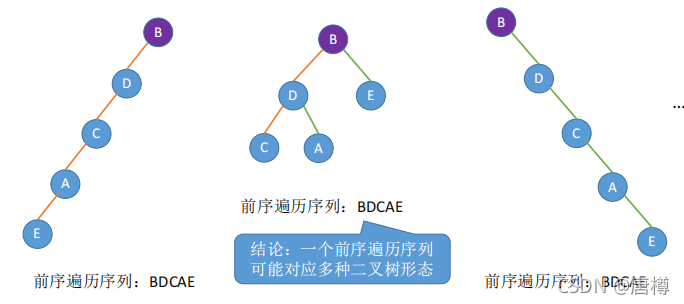
BDCAE的后序遍历:前序遍历左子树、前序遍历右子树、根结点。
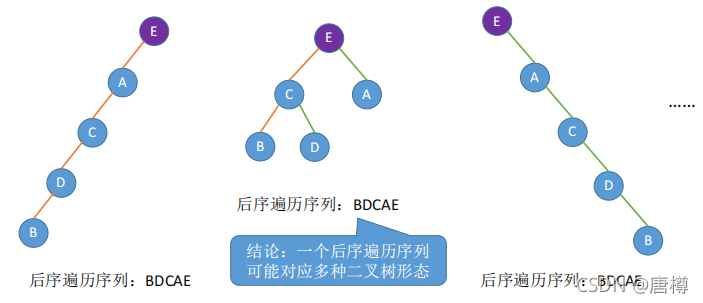
层序遍历序列也是同理。
所以结论: 若只给出一棵二叉树的 先、中、后、层 序遍历序列中的一种,不能唯一确定一棵二叉树。
二、两种遍历确定二叉树?
2.1 先序 + 中序遍历序列
先序遍历可以推出根节点,中序序列确定左右子树。
例如:
前序遍历序列:A D B C E
中序遍历序列:B D C A E
【分析】:A为根节点,(BDC)为左子树,(E)为右子树;
然后还剩下:(BDC)序列:
前序遍历序列:D B C
中序遍历序列:B D C
【分析】:D为根节点,B为左子树,C为右子树。
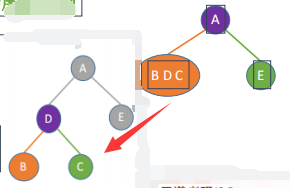
最后验证一下二叉树的先序与中序是否跟原条件一样。
例如:
先序遍历序列:D A E F B C H G I
中序遍历序列:E A F D H C B G I
根节点为D,左子树(E A F),右子树(H C B G I) ;
1、对左子树(E A F):
先序遍历序列:A E F
中序遍历序列:E A F
根节点A,左E,右F;
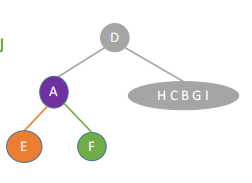
2、对右子树(H C B G I):
先序遍历序列:B C H G I
中序遍历序列:H C B G I
根节点B,左HC,右GI;
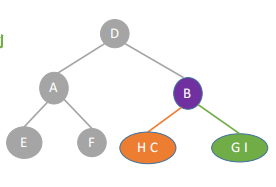
3、对HC:
先序遍历序列:C H
中序遍历序列:H C
根为C,左H;
4、对GI:
先序遍历序列:G I
中序遍历序列:G I
根G,右I;
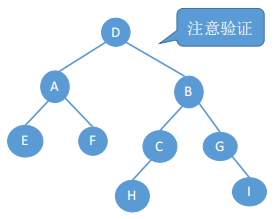
二叉树如下图所示:
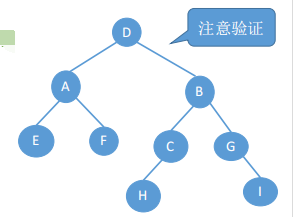
2.2 后序 + 中序遍历序列
同理,后序的最后一个是根节点,中序序列确定左右子树。
例如:
后序遍历序列:E F A H C I G B D
中序遍历序列:E A F D H C B G I
D为根节点,左(E A F),右( H C B G I)
1、对左子树(E A F):
后序遍历序列:E F A
中序遍历序列:E A F
根节点A,左E,右F;
2、对右子树(H C B G I):
后序遍历序列:H C I G B
中序遍历序列:H C B G I
根节点B,左HC,右GI;
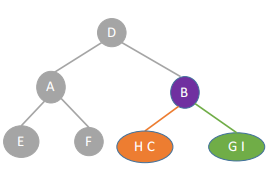
3、对HC:
后序遍历序列:H C
中序遍历序列:H C
根为C,左H;
4、对GI:
后序遍历序列:I G
中序遍历序列:G I
根G,右I;
2.3 层序 + 中序遍历序列
层序遍历第一个为根节点,中序序列确定左右子树。
例如:
层序遍历序列:A B C D E
中序遍历序列:A C B E D
根结点A,左为空NULL,右为(C B E D);
1、右为(C B E D);
层序遍历序列:B C D E
中序遍历序列:C B E D
根B,左C,右ED;
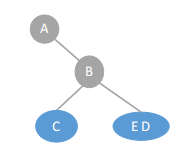
2、右ED:
层序遍历序列:D E
中序遍历序列:E D
根为D,左为E。