一、概念
?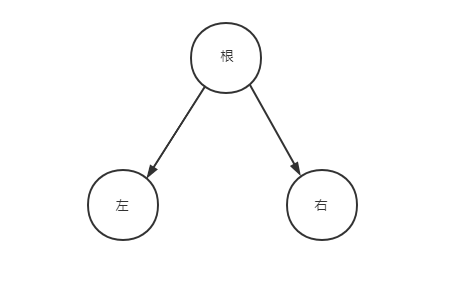
二叉树:一个根节点,两个子节点(子节点可能没有)。
--整篇文章内容中,左侧的子节点简称左,右侧的子节点简称右,根节点简称根。--
前序(先序)遍历:按根左右的顺序输出。
中序遍历:按左根右的顺序输出。
后序遍历:按左右根的顺序输出。
二、入门练习
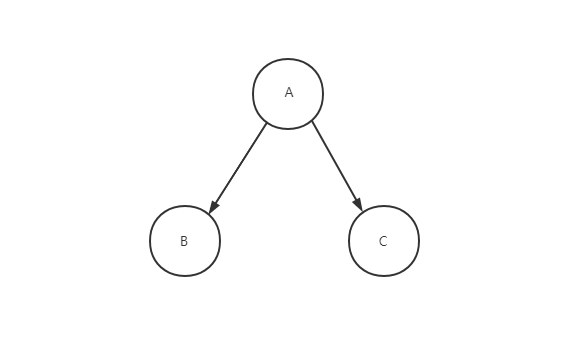
如上图这样一个简单的二叉树,我们分别输出三种遍历:
前序遍历:按ABC(根左右)的顺序输出。
中序遍历:按B|A|C(左根右)的顺序输出。
后序遍历:按BCA(左右根)的顺序输出。
比较特殊的是前序和后序。前序中,第一个输出是整棵树的根节点;后序中,最后一个输出是整棵树的根节点。记牢这两点,非常好用。
三、进阶练习
已知,前序遍历: GDAFEMHZ,中序遍历: ADEFGHMZ。画出二叉树图形,并输出后序遍历。
解题顺序:先画出二叉树图形,然后按照图形进行后序遍历。
1.根据前序遍历,我们可知G点是整棵树的根节点。那我们就可以这样分:
前: |G|? DAFEMHZ
中: ADEF? |G|? HMZ
从中序中可以直接的看出,G的左边都是它的左子树下的,G的右边都是它右子树下的。
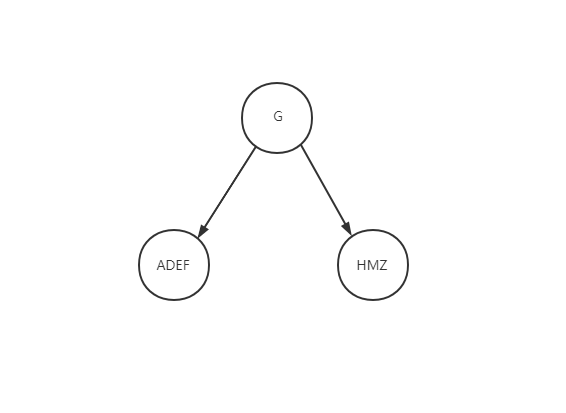
2.接下来,只看G左边部分?
前: G? |D|? AFEMHZ
中: A? |D|? EF??G??HMZ
前序中D是第一个,也就是根节点,中序中D把剩下来的内容分出了左右。
?
?3.因为左侧的A只分出来一个,说明A下面没有子节点了,我们只需要继续分右侧的EF
前: G? D??A??|F| EMHZ
中: A? ?D ?E? |F|??G??HMZ
同样的,我们从前序中发现,F是第一个,也就是说F是根节点;在中序中,E在F的左侧,说明E是F的左子树。
?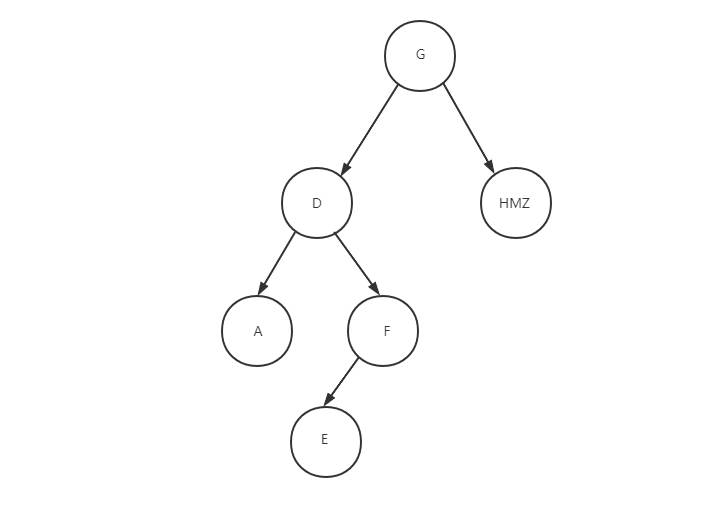
?4.这个时候G的整个左子树都确定好了,轮到右子树了。
?前: G? ?D??A??F??E? |M| HZ
中: A? ?D ?E? F? ?G??H |M| Z
从前序中,我们可以确定M是右侧的根节点,中序被M分成了左右各一个,说明H和Z正好是M的左右子树。
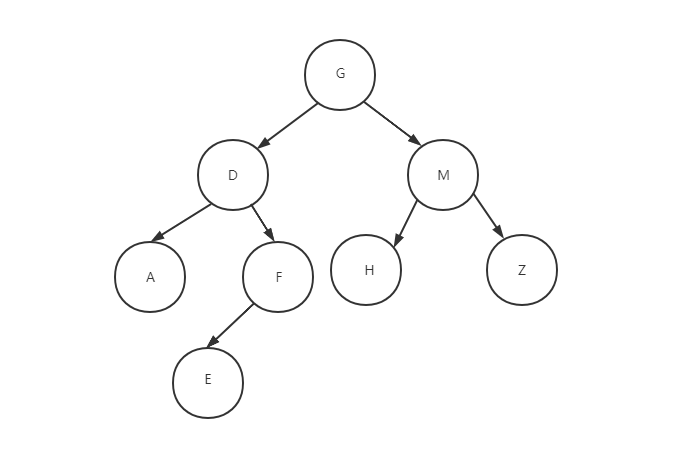
??5.总结
?通过以上步骤,我们可以发现,先从先序中确定根节点,再通过根节点,看中序中被分割后的位置,判断出节点对应左右子树位置。
6.输出后序
后序是左右根,那我们就看图,找最左边(不一定是最底层)的那一个。
1.从GDM看,左边是D,从DAF看,左边是A,到A就没有然后了。输出结果:A
2.找完左,在以A为子节点的二叉树(DAF)中,找到同级(同一个根节点下)的右子树,存在F,这个时候回到1步骤,从FE找左,就是E,到E没有然后了。输出结果:AE
3.找完左,在以E为子节点的二叉树(FE)中,找到同级的右子树,不存在,没有输出项。
4.FE二叉树的左右都输出了,输出根F。输出结果:AEF
5.DAF二叉树的左右都输出了,输出根D。输出结果:AEFD
6.GDM的左找完了,找右子树,存在M,继续找MHZ的左,就是H,到H就没有然后了。输出结果:AEFDH
7.找完左,在以H为子节点的二叉树(MHZ)中,找到同级的右子树,存在Z,到Z就没有然后了。输出结果:AEFDHZ
8.MHZ二叉树的左右都找完了,输出根M。输出结果:AEFDHZM
9.GDM这层的左右都找完了,输出根G。输出结果:AEFDHZMG
整个逻辑,就是递归
后序:递归输出左,递归输出右,递归输出根。
前序:递归输出根,递归输出左,递归输出右。
中序:递归输出左,递归输出根,递归输出右。