递归概述

百度百科：
程序调用自身的编程技巧称为递归（ recursion）。递归做为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回(即回溯)。
简单来说：
递归就是一种编程技巧，一般出现在一个函数体中，他最主要的特征就是这个函数会在执行过程中会调用自己，就是自己调用自己，本质也是一种循环。

借一个阶乘的例子来理解

如实现n的阶乘
阶乘：n的阶乘=n*(n-1)*(n-2)*…*1
阶乘的实现：
在这里插入图片描述
要理解递归，就要明白递归一般有两个步骤，即递归和回溯
递归的过程就是把参与递归的函数先全部展开运行的过程
回溯的过程就是将递归产生的结果进行处理
递归过程中也可能会出现回溯，回溯过程中也会出现递归。(这里后续的迷宫回溯和八皇后会有涉及到)

比如上面的阶乘，假设n为3，函数开始运行的时候，首先他会持续递归，
首先变成3*Factorial(2)，然后继续递归，Factorial(2)变成2*Factorial(1)，然后继续递归，Factorial(1)变成1，此时，只剩下最外层的一个函数，递归过程结束，此函数的值此时由3*Factorial(2)变成了3*2*1，然后开始回溯，即，将这些函数的值进行最后的操作，这里即乘在一起得出最后的结果

递归实现找到迷宫出口

这里我们创建一个二维数组来表示迷宫地图
然后对迷宫初始化
设置墙壁，将点值设置为1表示墙壁
设置可走的路，将点值设置0表示此点可以行走
在这里插入图片描述
这里搞一个8*7的地图，简单设置两个路障
这里把地图设置简单点是为了方便理解和设置，不要觉得这个程序垃圾，这玩意，无论多难的地图，都能给解出来，此处我们是来学习他的核心思想的，不是来解地图的，这只要搞会，啥地图都没问题。只是可能费时间（小声哔哔)
设立规则：
设置起始点，在起始点的基础上对其下标(索引)进行加减，以此来当做点的前后左右移动
走过的点用2标记，未走过的用0标记，死点(无法向0点移动的点)用3标记，、
设置每次移动方式的优先级为：下>右>上>左。即每次先尝试级别高的移动方式，若无法移动再尝试级别低的
设置当点到达某一位置的时候算到达出口，此处简单的设置为map[4][5]点

实现

首先得到刚才的地图
然后单独写一个类，此类用于实现迷宫问题和地图的打印
地图打印
然后开始实现找出口的函数，此函数接收三个参数，当前点的位置和代表地图的二维数组
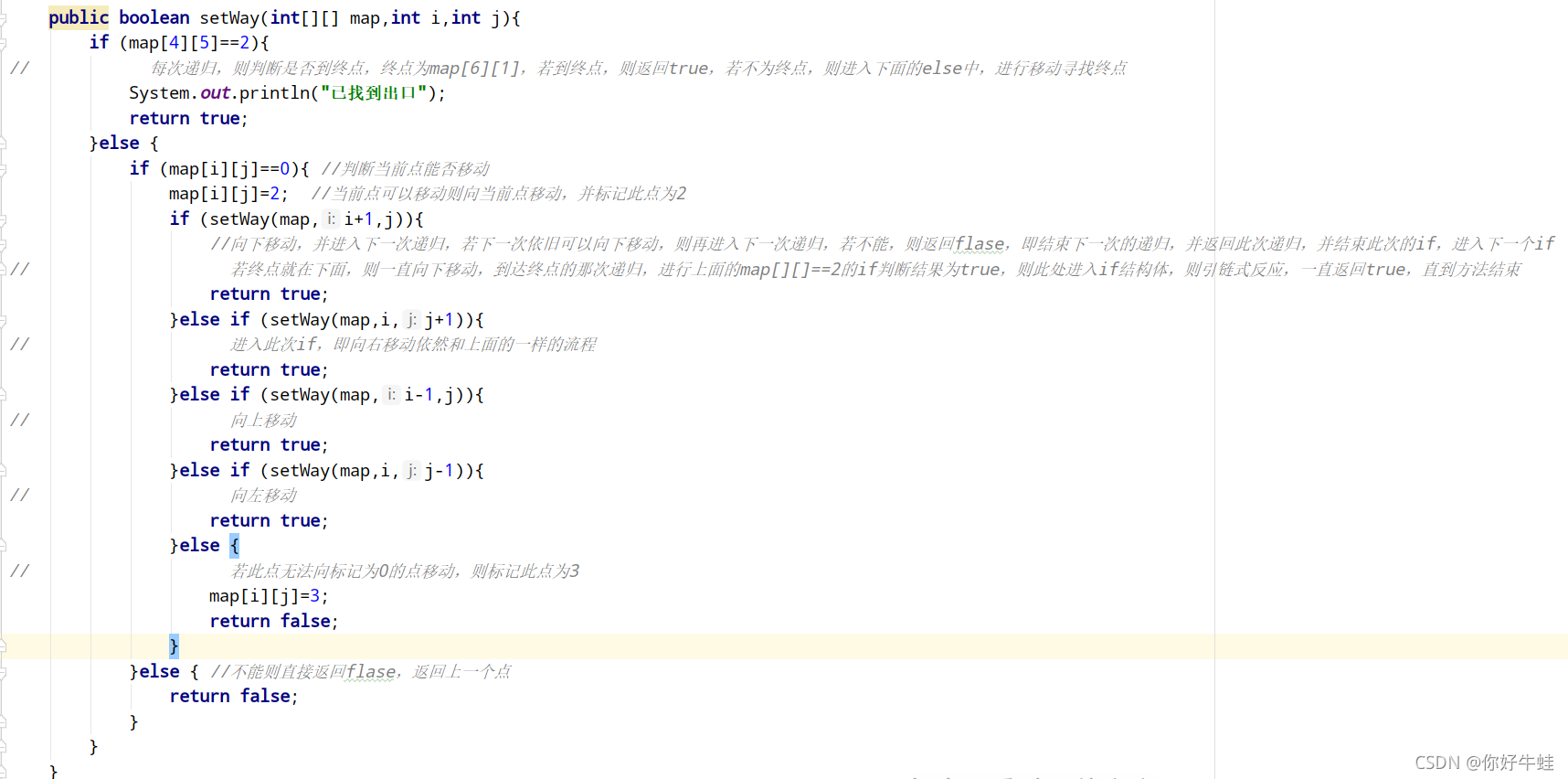
然后最难的地方来了，为什么难？因为找出口这部分代码的东西实在太不好理解。代码就那么点，要是理解了，一切就非常简单。我们先来分析整体的设计思路
这里，我们要找到迷宫的出口，就得借助递归的特性。这里也是一种巧妙的递归，此函数体中的一切，都是为了进行递归而巧妙设计的
思路：
在寻找出口的过程中，我们先尝试一直向下移动，若撞到墙壁则往右，然后若再次撞到墙壁则往上，然后若再撞到墙壁则再往左。每次移动结束后，我们把此时所在的点标记为2，我们设置，每次不可以向标记为2的地方移动。若到达某点后，其上下左右都无法移动，则把此点标记为3，然后退回到上一个点(此处是退回，不是移动，所以不用在意不能向标记为2地点移动的规则)，在上一个点的基础上再进行移动。我们设置，也不可以向标记为3的地点移动。每次移动结束，并标记当前点为2结束后，都判断是否找到出口，若找到出口，则结束寻找，若未找到，则继续移动。
代码的理解：
知道这些思路后，我们结合思路来看代码。
首先我们看点在迷宫中的移动方式，这里用递归来模拟移动

这里，每次递归就进行一次移动，每次点的移动即在当前点的索引上把某个坐标值减1或加1。移动后的坐标直接作为新的参数传入下次递归的函数体中，这里四个if语句，表示四种移动方式，if结构体中的return true用于回溯的时候，当找到出口，则进入到这里面
首先，每进入一次递归，便判断上一次移动的点是否是出口，即判断map[4][5]是否为2，这是找到出口的判决条件

然后后面，未找到出口，则先判断此时点所处的位置是否是可以到达的位置：

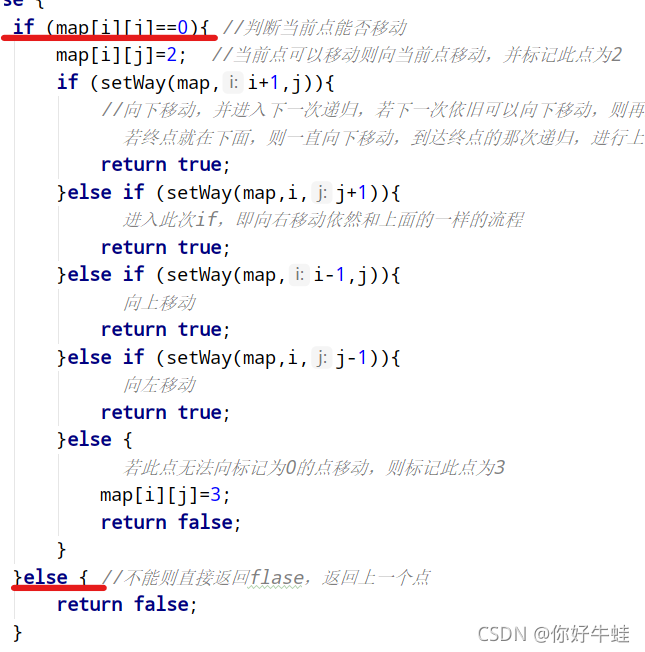
这里只看红线部分就行。用一个if语句来判断，当此时所处点状态不为0，则表示此点不能走，则进入else语句，返回flase，便退出此次递归，回到上一次递归。
至此其实最重要的找寻出口的部分已经结束，这个代码精妙之处就在于他拆开看，啥都看不懂，但合在一起，真的是妙蛙种子吃着妙脆角妙进了米奇妙妙屋，秒到家了！
这里也是分为递归和回溯两部分，首先，点进行移动，每次移动都是一次递归，先朝着一个方向使劲递归，像极了不撞南墙不回头的我们，直到撞到墙，知道疼后，才懂得退后，正好退后的操作，就是最后返回false的那一部分，这里回溯到上一次递归，这里有着四次的if-else结构体，四种选择，一个方向不行，换一个方向来横冲直撞，再次遇到痛，这次我们运气好，找到了出口，然后返回true，正好让此条if-else语句执行，然后呢，他也返回true，然后就跟多米诺骨牌，哗！一下，全部返回true，这就是瞬间的回溯，一下子退出了所有的递归，就找到出口了。

全部代码

import java.util.Map;

public class mazeDemo {
    public static void main(String[] args) {
//        创建二维数组
        int[][] map=new int[8][7];
//        初始化
        for (int i = 0; i < 8; i++) {
            map[i][0]=1;
            map[i][6]=1;
            if (i<7){
                map[0][i]=1;
                map[7][i]=1;
            }
        }
        map[5][5]=1;
        map[5][1]=1;


        Maze maze=new Maze();
//        展示初始地图
        maze.showArray(map);
//        设置起点
        maze.setWay(map,1,1);
//        展示找到结果后的地图
        maze.showArray(map);
    }
}
class Maze{


//    整体思路：设置起始点，在起始点的基础上进行加减，以此来当做点的前后左右移动
//    走过的点用2标记，未走过的用0标记，死点(无法向0点移动的点)用3标记
//    其实整体来看，递归也是一种循环，一直循环同一个方法体
//    这里一直递归，每次移动都调用一下方法体本身，即递归一次
//    假设一个方向撞墙，则在此点的基础上进行其他方向的移动
//    若此点无法移动，为死点，则返回上一个点，在上一个点的基础上再进行移动
    public boolean setWay(int[][] map,int i,int j){
        if (map[4][5]==2){
//            每次递归，则判断是否到终点，终点为map[6][1]，若到终点，则返回true，若不为终点，则进入下面的else中，进行移动寻找终点
            System.out.println("已找到出口");
            return true;
        }else {
            if (map[i][j]==0){ //判断当前点能否移动
                map[i][j]=2;  //当前点可以移动则向当前点移动，并标记此点为2
                if (setWay(map,i+1,j)){
                    //向下移动，并进入下一次递归，若下一次依旧可以向下移动，则再进入下一次递归，若不能，则返回flase，即结束下一次的递归，并返回此次递归，并结束此次的if，进入下一个if
//                    若终点就在下面，则一直向下移动，到达终点的那次递归，进行上面的map[][]==2的if判断结果为true，则此处进入if结构体，则引链式反应，一直返回true，直到方法结束
                    return true;
                }else if (setWay(map,i,j+1)){
//                    进入此次if，即向右移动依然和上面的一样的流程
                    return true;
                }else if (setWay(map,i-1,j)){
//                    向上移动
                    return true;
                }else if (setWay(map,i,j-1)){
//                    向左移动
                    return true;
                }else {
//                    若此点无法向标记为0的点移动，则标记此点为3
                    map[i][j]=3;
                    return false;
                }
            }else { //不能则直接返回flase，返回上一个点
                return false;
            }
        }
    }
    public void showArray(int [][] map){
//        遍历二维数组
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[i].length; j++) {
                System.out.print(map[i][j]+" ");
            }
            System.out.println();
        }
    }
}

八皇后

概述

问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。
说是八皇后，但我们这里只要你电脑配置够，我们可以实现n皇后
找个图：
在这里插入图片描述源自百度

实现

咱先把8行的棋盘，从下往上，分别是第一行到第八行，从左到右是第一列到第八列。首先，咱知道，一行中是肯定不能摆放大于一个的皇后了。
思路：
把棋盘上每一种摆放方式都试一遍
大致思路：
先找到每行棋子最靠左的可行的摆放方式，然后在依次更改后面行的摆放位置，先从第8行开始，从左到右一格一格的试，试到最右边，然后更换第7行的摆放位置，将其向后移动一位，然后再把第8行的棋子从1列到8列一格一格的试。第8行试完，再第七行再向后移动一位，再低8行从1列到8列的试。直到7行移动到最右边，然后移动第6行的，重复上述操作，直到第一行的试完。至此便能找到所有的结果。
进一步的思路：
编写一个方法体，用于判断所有皇后是否冲突。每次移动一次棋子，都进行一次判断，设置一个变量当做计数器，不冲突则让自变量自增1。
编写判断皇后冲突方法的思路：
邓小平爷爷说过，黑猫白猫，抓到老鼠的就是好猫。
我们这里为了方便，不再使用二维数组来替代棋盘，我们用一个一维数组来替代棋盘。
此一维数组的索引代表棋盘的第几行，索引对应的值，即checkerboard[索引]代表第几列。
然后这样，来判断是否冲突就简单多了，后续对棋子的移动也很简单。
来看方法体的具体实现：
在这里插入图片描述
看注释讲解。我太累了，不想再整理一遍了
然后我们还要准备一个打印棋盘的方法

为了简单，此处直接打印一维数组，不将其转换为二维数组再打印了
然后就是核心部分，此处思路：
利用递归的特性，我们每摆放一行就是一次递归，首先找到第一种摆放方式，此时是递归了8次，然后开始回溯。在回溯过程中，用for循环来表示棋子在一行上从1到8的运动测试。
如何判断某次递归是否是第八行摆放皇后？
递归的方法体接收一个整形参数，我们第一次自己调用此方法体我们传入一个初始值，0，然后在递归的时候，每次递归我们都让这个值加一然后传入这个方法体，同时每次递归都判断此值是否到达了8，如果为8则表示，最后一行也已经摆放完成。
核心代码部分
在这里插入图片描述就这么点，show是我们编写的打印棋盘的方法，judge是我们判断当前皇后和前面皇后是否冲突的方法。这个是我去掉注释的版本，后面放出一个有注释的

这里面的if(n=max)用于判断是否完成一次摆放，是的话，把计数器count自增1。然后跳出此次递归，回溯到上一次，继续向后寻找下一种可能。
若不是一种可行的方式，后面一个for循环，把当前棋子向后移动一位(移动操作即checkerboard[n]=i)，然后进入下一次递归，在下一次递归中正好判断是否完成一次摆放。如此，一直递归。这里的for选混非常巧妙，他承担着在回溯过程中最重要的角色。第一次摆放方式找到后，此时方法体中会有8个未完成的for循环，这里的回溯，主要的就是执行这些for循环，每次for循环中的每次执行，都又会开创一次递归，每次的递归又会出现回溯，至此，疯狂的扩张，线性增长，便能触及到所有的结果。触及到所有的结果后，正好我们有一个判断if(n=max)卡着他，让他不至于扩张的太过分，然后所有的扩张结果又会全部回到原点，至此得到全部结果。

正好按照上面的思路来，正好得到第一种摆放方式的时候，正好n等于8，此时便开始回溯。这里有一个小细节：我们的n是从0开始的，当n等于8的时候n是自增了9次，但是按道理我们是只需要递归8此啊？下面解释：此方法体中对n的涉及顺序是：先判断(判断是否到我们想要的结果)，然后再自增(即递归传值)。所以当我们n等于7，此时是第8次的递归(即最后一行的摆放)，然后按照方法体的设计，此时会再次进入一次递归，此时n便变成8了，正好符合我们的判决条件，然后退出这次的方法体，下面的递归便不会再执行，所以总的来说还是正好把8行给摆放完成。

带注释的全部代码

一定要多看注释！！！

public class EightQueensDemo {
    public static void main(String[] args) {
        EightQueens queens=new EightQueens(8); //传入8，我们先求8皇后的问题。传入n便求n皇后
        queens.put(0);  //固定值，传入初始值0，就跟燃油汽车只能添加汽油一样，此处只能传入固定值0才能正常运行
        System.out.println("共有"+queens.getCount()+"摆放方式");
    }

}
class EightQueens{
    private int count=0;
    private int max;  //这里的max代表棋盘规格和几个皇后
    private int[] checkerboard;
    public EightQueens(int max) {
//        求任意数量皇后的问题把传入为对应的值即可
        this.max = max;
//        同时初始化棋盘
        checkerboard=new int[max];
    }


//    用一个一维数组来表示棋盘，索引代表第几行，checkerboard[索引]代表第几列

    private boolean judge(int n){
//        判断第n个皇后和前面的所有皇后是否冲突
        for (int i = 0; i < n; i++) {
//            i和n代表第几行，checkerboard[i]和checkerboard[n]代表第几列
            if (checkerboard[i]==checkerboard[n]||Math.abs(n-i)==Math.abs(checkerboard[n]-checkerboard[i])){
//                checkerboard[i]==checkerboard[n]表示在同一列上。
//                以i所在那一行为底，n所在那一列为高，i、n和高和底的交点为定点作三角形，
//                则Math.abs(n-i)表示三角形的高长，Math.abs(checkerboard[n]-checkerboard[i])表示三角形的底长
//                若Math.abs(n-i)==Math.abs(checkerboard[n]-checkerboard[i]则表示这是一个等腰直角三角形,即i和n两点在同一条45度斜线上
                return false;
            }
        }

//        不用判断是否在同一行，后面程序设计上会自动避免这个问题
        return true;
    }


    public int getCount() {
        return count;
    }
    //    整体思路：
//    用一个一位数组来代表棋盘，一维数组的索引表示第几行，和该放第几个皇后，他的每个索引对应的值表示在当前行上的第几列
//    然后准备开始放置，在每次放置前，先判断是否已经摆放了8个皇后
//    开始放置，这里用暴力放置法，每行的每个格子都试一遍，尝试试出所有的放置方法
//    通过for循环和递归和递归的回溯来实现
//    for循环用来表示某一行的所有格子的放置，递归表示进入下一行的放置，回溯表示回到上一行的放置
//    首先把第0个皇后(我们从0开始)放在第0行第0列上，然后进行下一行的放置，找到合适位置，则继续进行其他行的放置尝试，若某一行找不到合适的位置，则进行回溯，回溯到上一行从新找其他的合适位置
//    若都能找到，即找打了一个正确的放置，则开始进行回溯。每次回溯到第0行，则表示第0行的此次for循环，即第0个皇后在此处的放置(每次for循环都是在此行的一处放置)，其他皇后已经找到了所有可能放置方法
//    然后进入下一个位置的放置，即for循环

    //回溯原理：
//    假设最后一行找到了一个正确的摆放位置，但是此时for循环未停止，则会继续for循环，继续在最后一行向后寻找正确的摆放位置，若最后一行找到头了，即for循环结束了
//    则回溯到上一行，上一行则再重新向后找一个正确的摆放位置，
//    若找到了，则再递归到最后一行，此时上一行是一个新的正确摆放位置，再这样的条件下，在最后一行再从第0个格子重新再寻找正确摆放位置，再把最后一行遍历一遍
//    若未找到，则返回上上行，再在上上寻找一个新的正确的摆放位置，再重复后面行的重新寻找正确摆放位置的操作，一直套娃，一直回溯递归
    public void put(int n){
//        每次递归或回溯，判断是否8个皇后全部放好
        if (n==max){
            count++;
            show();
//            如果8个已经放好，则跳出这次递归，进行回溯，进行上一次递归未运行完的for循环
            //这里，每次到这里其实第n个皇后还未摆放，因为后面每次传入的参数是n+1，这里只是判断，还并未真正摆放
            // 因为n是从0开始的，所以到这里也是已经摆放了8个
            return;
        }
        for (int i = 0; i < max; i++) {//每次递归都会有这一个的8次的for循环，来尝试在此行的每一个格子上放置皇后
//            这里有8此循环，下面放皇后，放在第i个格子上。正好8此循环，就等于把皇后在同一行上的所有格子都试一遍
//            每次n递增，正好n可同时表示该放第几个皇后，和放在哪一行
            checkerboard[n]=i;

//            每次放好后，进行判断，是否与其他的皇后冲突
            if(judge(n)){  //若不冲突，则进入下一次递归，即进入下一行的放置尝试
                put(n+1);
            }else {
//                若冲突，则跳过此次for循环，进入下次循环，即把该皇后在此行上向后移一位(即i+1，i表示列，n表示行)
//                若这一行都试完了(即for循环结束了)，都不行，则此次的递归就会自动结束了(循环运行完了，代码运行完了)，
//                然后回溯到上一次的递归(就等于回到了上一行)，跳过此行中皇后放置正确的那一次for循环，继续for循环，寻找下一个在这一行可以正确防止皇后的位置
//                若找到了，则又进入递归，再重复上面的过程。若一直没找到，则再次回溯的更上面的行。
                continue;
            }
        }
    }

    private void show(){
//        打印棋盘，此处即一维数组
        System.out.print("一种摆放方式是：");
        for (int i = 0; i < checkerboard.length; i++) {
            System.out.print(checkerboard[i]+" ");
        }
        System.out.println();
    }
}