[数据结构与算法]LeetCode-每日一题 223. 矩形面积 [Java实现]

给你 二维 平面上两个 由直线构成的 矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其 左下 顶点和 右上 顶点坐标表示：

• 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。
• 第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。
  ?

示例 1：

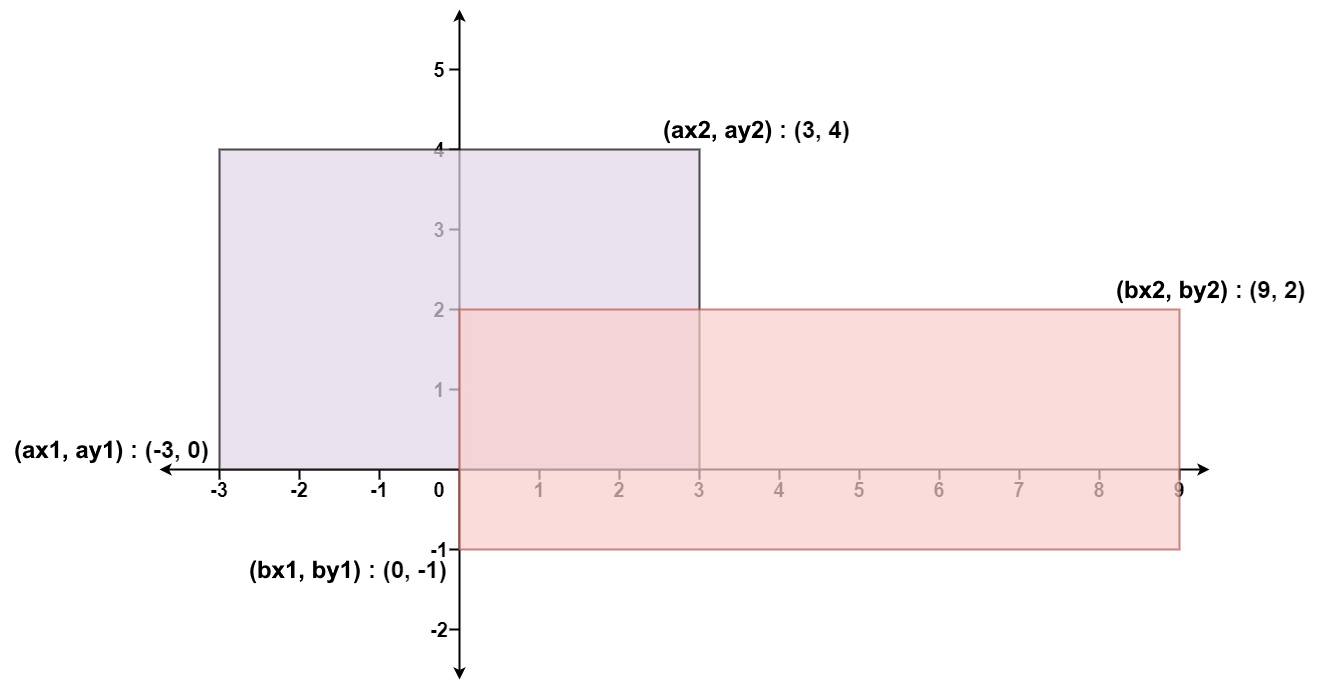
输入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出：45

方法一：容斥原理

我们可以利用容斥原理，先分别计算两矩形的面积和，然后减去重叠部分面积。而对于重叠部分面积，我们可以这样计算：

1. 设两矩形左下，右上坐标分别为 (A, B) (C, D) 与 (E, F) (G, H)
2. 判断第二个矩形是否在第一个矩形的 上 / 下 / 左 / 右 方且无交集
   1. 若在上方 则有 F >= D (第二个矩形的最低y坐标 >= 第一个矩形的最高y坐标)
   2. 若在下方 则有 B >= H
   3. 若在左方 则有 A?>= G
   4. 若在右方 则有 E >= C

    public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int overArea = 0;
        if (!(F >= D || B >= H || A >= G || E >= C)) {
            overArea = (Math.min(C, G)-Math.max(A, E)) * (Math.min(D, H)-Math.max(B, F));
        }
        return (C-A)*(D-B) + (G-E)*(H-F) - overArea;
    }