一、前言
1.1、前言
此博客虽然为转载,但代码大部分都是我自己写的,加上了自己的一些思路和注解,希望大家能喜欢,点个赞再走呗,多谢!!
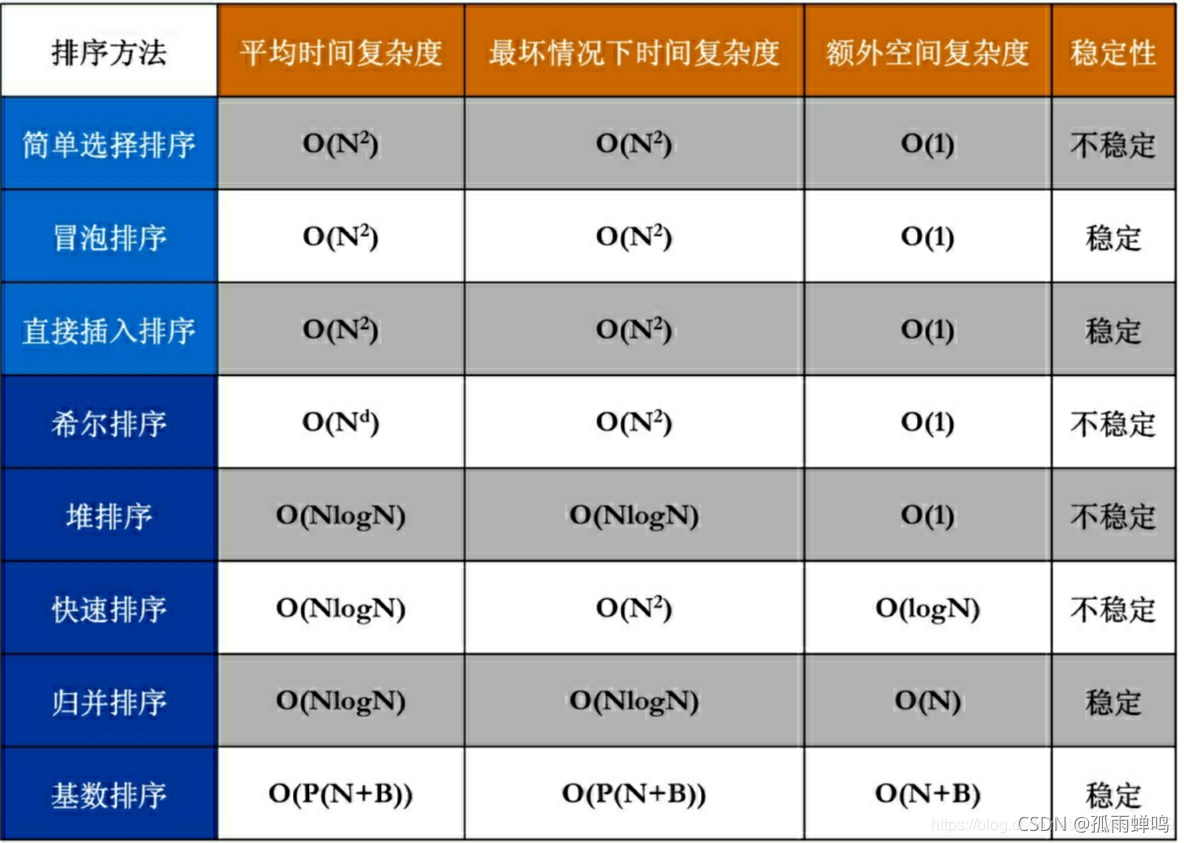
1.2、复杂度
1.3、算法稳定性
排序算法的稳定性大家应该都知道,通俗地讲就是能保证排序前两个相等的数据其在序列中的先后位置顺序与排序后它们两个先后位置顺序相同。即:如,如果A i == A j,Ai 原来在 Aj 位置前,排序后 Ai 仍然是在 Aj 位置前。
选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法
冒泡排序、插入排序、归并排序和基数排序都是稳定的排序算法
二、冒泡排序
2.1、思路:
1 、比较相邻的元素,如果第一个比第二个大,就交换它们两个;
2、对每一对相邻元素作相同的工作,从开始第一对到结尾的最后一对,这样在最后的元素就是最大的数;
3、排除最大的数,解这下一轮继续相同的操作,确定第二大的数…
3、重复步骤1-3,直到排序完成。
2.2、动画演示:

2.3、实现代码
package com.chan.sort;
/**
* 冒泡排序(升序)
* @author lone_wolf
* @version 1.0
* @date 2021/9/29 14:52
*/
public class BubbleSort {
private static int[] sort(int[] a) {
//排序n次,是必须的
for (int i = 0; i <a.length; i++) {
for (int j = 0; j < a.length-i-1; j++) {
if (a[j]>a[j+1]){
int temp = a[j];
a[j] = a[j + 1];
a[j+1] = temp;
}
}
}
return a;
}
private static void print(int[] a){
for (int i : a) {
System.out.print(" "+i);
}
System.out.println();
}
public static void main(String[] args) {
int[] a = {6,1, 2, 5, 3, 4};
print(a);
sort(a);
print(a);
}
}
结果:
6 1 2 5 3 4
1 2 3 4 5 6
2.4、总结
平均时间复杂度:O(n2)
空间复杂度:O(1)
算法稳定性:稳定
三、插入排序
3.1、思路
1、从第一个元素开始,该元素可以认为已经被排序;
2、取出下一个元素,在前面已排序的元素序列中向前扫描;
3、如果该元素(以拍下)大于新元素,将该元素移动下一位置;
4、重复不走3、直到找到已排序的元素小于或者等于新元素的位置;
5、将新元素插入到该位置后;
6、重复步骤2-5。
3.2、动画演示

3.3、实现代码
package com.chan.sort;
/**
* 插入排序(升序)
* @author lone_wolf
* @version 1.0
* @date 2021/9/29 15:23
*/
public class InsertSort {
private static int[] sort(int[] a) {
for (int i = 1; i < a.length; i++) {
int temp = a[i];
//j要取出,用于最后的将新元素插入到该位置后
int j = i-1;
for (; j >= 0; j--) {
if (a[j] > temp) {
//如果该元素(已排序)大于新元素,将该元素移到下一位置
a[j + 1] = a[j];
}else {
//直到找到已排序的元素小于或者等于新元素的位置
break;
}
}
//将新元素插入到该位置后
a[j+1] = temp;
}
return a;
}
private static void print(int[] a) {
for (int i : a) {
System.out.print(" " + i);
}
System.out.println();
}
public static void main(String[] args) {
int[] a = {6, 1, 2, 5, 3, 4};
print(a);
sort(a);
print(a);
}
}
结果:和冒泡一致,后不再展示结果。
3.4、总结
平均时间复杂度:O(n2)
空间复杂度:O(1)
算法稳定性:稳定
四、选择排序
4.1、思路
1、第一轮,找到最小的元素,和数组第一个数交换位置
2、第N(N<n)轮,找到第二小的元素,和数组第N(N<n)个数交换位置
3、直到最后一个(n)元素,排序完成
4.2、动画演示

4.3、实现代码
package com.chan.sort;
/**
* 选择排序(升序)
*
* @author lone_wolf
* @version 1.0
* @date 2021/9/30 10:09
*/
public class SelectSort {
public static int[] sort(int[] a) {
//标志位用不到最后一位,故比较次数为(a.length-1),其实也随便,a.length也对,只不过下面j=i+1会直接跳出循环
for (int i = 0; i < a.length - 1; i++) {
//将第i个数下标存起来,用于比较最小值再替换,为什么不存值,可以看我下面if条件后注释的地方
int min = i;
for (int j = i + 1; j < a.length; j++) {
/*为什么这里不存min=a[j]这么写,主要因为出了循环后还要进行最小值与第i个值的替换
无法确定之前j的位置,因为此时出了循环后j就等于a.length了
if (a[j] < min){
min = a[j];
}*/
if (a[j] < a[min]) {
min = j;
}
}
//出了循环后要开始替换
if (min != i){
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
return a;
}
/**
* 用于继承
*/
public static void print(int[] a) {
for (int i : a) {
System.out.print(" " + i);
}
System.out.println();
}
public static void main(String[] args) {
int[] a = {6, 1, 2, 5, 3, 4};
print(a);
sort(a);
print(a);
}
}
4.4、总结
平均时间复杂度:O(n2)
算法空间复杂度:O(1)
算法稳定性:不稳定
五、希尔排序
5.1、思路
1、把数组分割成若干(h)个小组(一般数组长度length/2),然后对每个小组分别进行插入排序;
2、每一轮分割的小组的个数逐步缩小,h/2->h/4->h/8,并且进行排序,保证有序。当h=1时,则数组排序完成
5.2、动画演示

5.3、实现代码
package com.chan.sort;
/**
* 希尔排序(升序)
* @author lone_wolf
* @version 1.0
* @date 2021/9/30 10:50
*/
public class ShellSort extends SelectSort{
public static int[] sort(int[] a) {
int gap = a.length /2;
while (gap>0){
for (int i = gap; i < a.length; i++) {
//这里把a[i]存起来
int temp = a[i];
int index = i - gap;
while (index >=0 && a[index] > temp){
a[index + gap] = a[index];
index -= gap;
}
//这里相当于置换,利用插入排序,每次都用的是插入排序方法,可以借鉴我前面写的插入排序,是一样的思路
//我插入排序的gap只不过是1而已
a[index + gap] = temp;
}
gap /=2;
}
return a;
}
public static void main(String[] args) {
int[] a = {6, 1, 2, 5, 3, 4};
print(a);
sort(a);
print(a);
}
}
5.4、总结
平均时间复杂度:O(nlogn)
算法空间复杂度:O(1)
算法稳定性:稳定
六、快速排序
6.1、思路
快排,面试最喜欢问的排序算法,这是运用分治法的一种排序算法
1、从数组中选一个数作为基准值,一般选第一个数,或者最后一个数
2、采用双指针(头尾两端)遍历,从左往右找到比基准值大的第一个数,从右往左找到比基准值小的第一个数,交换两数位置,直到头尾指针相等或头指针大于尾指针,把基准值与头指针的数交换。这样一轮之后,左边的数就比基准值小,右边的数就比基准值大
3、对左边的数列,重复上面1,2不走。对右边重复1,2步骤
左右两边数列递归结束后,排序完成(即递归左边数据为1位或右边数据为1位)
6.2、动画演示

6.3、实现代码
package com.chan.sort;
/**
* 快速排序(升序)
*
* @author lone_wolf
* @version 1.0
* @date 2021/9/30 16:07
*/
public class QuickSort extends SelectSort {
public static void sort(int[] a, int start, int end) {
if (start > end) {
return;
}
int temp = a[start];
int i = start + 1, j = end;
//用于不结束循环
while (i < j) {
//从左往右遍历,若遇到第一个大于temp的数则退出并在后面记录该数
while (i < j && a[i] < temp) {
i++;
}
//从右往左遍历,若遇到第一个小于temp的数则退出并在后面记录该数
while (i < j && a[j] > temp) {
j--;
}
if (i < j) {
//此处用于交换数组,左边比基准数大的数和右边比基准数小的数相互交换
int item = a[i];
a[i] = a[j];
a[j] = item;
}
}
//此处判断i或者j两个指针不能超过start和end,若不判断则会出现数组越界异常
if (i <= end && j >= start) {
//此处为结束循环,说明此次排序结束,再做完下面两步,左边的数全比基准数小,右边的数全比基准数大
a[start] = a[j];
a[j] = temp;
//下一步进行递归,直到start > end
sort(a, start, i - 1);
sort(a, i + 1, end);
}
}
public static void main(String[] args) {
int[] a = {6, 1, 2, 5, 3, 4};
print(a);
sort(a, 0, a.length - 1);
print(a);
}
}
5.4、总结
平均时间复杂度:O(nlogn)
算法空间复杂度:O(1)
算法稳定性:不稳定
七、归并排序
7.1、思路
归并排序是也是采用分治法,并且是一种稳动的排序方式,不过需要使用到额外的空间
1、把数组不断划分成子序列,划成长度职业2或者1的子序列
2、然后利用临时数组,对子序列进行排序,合并,再把临时数组的值赋值回原数组
3、反复操作1~2步骤,直到排序完成
注意:只有"相邻同一组"的数组可以进行比较,我这句话会在代码中显现
7.2、动画演示

7.3、实现代码
package com.chan.sort;
import java.util.Arrays;
/**
* 归并排序(升序)
*
* @author lone_wolf
* @version 1.0
* @date 2021/9/30 17:05
*/
public class MergeSort extends SelectSort {
public static void sort1(int[] a, int[] b, int start, int end) {
if (start >= end) {
return;
}
//由于要多次使用,故而用此来接,显得代码更加清晰
int mid = (start + end) / 2;
//左递归,最小为1——一个数组的单位即a[i]
sort1(a, b, start, mid);
//右递归,最小为1——一个数组的单位即a[j]
sort1(a, b, mid + 1, end);
//合并,只有相邻同一组的数据才能合并,
//例如a[0]这一组会和a[1]这一组合并为一组,合成一组后才能和后面的a[2]、a[3]合并为一组后继续合并
// 归并排序就是这样的特点,可以利用这一点设计相应的递归操作,这一特点也可以根据图像动图看出
sort2(a, b, start, mid, end);
}
public static void sort2(int[] a, int[] b, int start, int mid, int end) {
//b数组的标志位,后面还要用于进行数组的复制操作
int index = 0;
//左边的数据(已排序)
int i = start;
//右边的数据(已排序)
int j = mid + 1;
//这里就是左边那一组的数据和右边那一组数据的比较并放入b数组中
while (i <= mid && j <= end) {
//小的放先放入b数组
if (a[i] < a[j]) {
b[index++] = a[i++];
} else {
b[index++] = a[j++];
}
}
//还没放完,只是把小的数据先放进了b数组里,故而还要进行判断
while (i <= mid) {
b[index++] = a[i++];
}
while (j <= end) {
b[index++] = a[j++];
}
//进行复制操作,浅拷贝,不懂参数咋填自己搜
System.arraycopy(b, 0, a, start, index);
}
public static void main(String[] args) {
int[] a = {6, 1, 2, 5, 3, 4};
//b数组长度必须和a数组目标数组一直,否则最后一次排序可能会超出数组范围
int[] b = new int[a.length];
print(a);
sort1(a, b, 0, a.length - 1);
print(a);
}
}
7.4、总结
平均时间复杂度:O(nlogn)
算法空间复杂度:O(n)
算法稳定性:稳定
八、堆排序
8.1、思路
大顶堆概念:每个节点的值都大于或者等于它的左右子节点的值,所以顶点的数就是最大值
8.2、动画演示

8.3、实现代码
package com.chan.sort;
/**
* @author lone_wolf
* @version 1.0
* @date 2021/9/30 21:46
*/
public class HeapSort {
public static void main(String[] args) {
int[] a = {6, 1, 2, 5, 3, 4};
sort(a);
for (int i : a) {
System.out.print(" " + i);
}
System.out.println();
}
protected static void sort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
heapSort(nums);
}
private static void heapSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
//构建大根堆
createTopHeap(nums);
int size = nums.length;
while (size > 1) {
//大根堆的交换头尾值,固定最大值在末尾
swap(nums, 0, size - 1);
//末尾的索引值往左减1
size--;
//重新构建大根堆,其实这里也可以用createTopHeap(),但大根堆大部分已经构建,再次构建效率直线下降
updateHeap(nums, size);
}
}
private static void createTopHeap(int[] nums) {
for (int i = 0; i < nums.length; i++) {
//当前插入的索引
int currIndex = i;
//父节点的索引
int parentIndex = (currIndex - 1) / 2;
//如果当前遍历的值比父节点大的话,就交换值。然后继续往上层比较
while (nums[currIndex] > nums[parentIndex]) {
//交换当前遍历的值与父节点的值
swap(nums, currIndex, parentIndex);
//把父节点的索引指向当前遍历的索引
currIndex = parentIndex;
//往上计算父节点索引
parentIndex = (currIndex - 1) / 2;
}
}
}
private static void updateHeap(int[] nums, int size) {
int index = 0;
//左节点索引
int left = 2 * index + 1;
//右节点索引
int right = 2 * index + 2;
while (left < size) {
//最大值的索引
int largestIndex;
//如果右节点大于左节点,则最大值索引指向右子节点索引
if (right < size && nums[left] < nums[right]) {
largestIndex = right;
} else {
largestIndex = left;
}
//如果父节点大于最大值,则把父节点索引指向最大值索引
if (nums[index] > nums[largestIndex]) {
largestIndex = index;
}
//如果父节点索引指向最大值索引,证明已经是大根堆,退出循环
if (largestIndex == index) {
break;
}
//如果不是大根堆,则交换父节点的值
swap(nums, largestIndex, index);
//把最大值的索引变成父节点索引
index = largestIndex;
//重新计算左节点索引
left = 2 * index + 1;
//重新计算右节点索引
right = 2 * index + 2;
}
}
private static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}//10万个数的数组,耗时:38毫秒
8.4、总结
平均时间复杂度:O(nlogn)
算法空间复杂度:O(n)
算法稳定性:不稳定
九、基数排序
9.1、思路
基数排序是一种非比较型整数排序算法
1、将整数按位数切割成不同的数字
2、然后按每个位数分别比较。
3、由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
9.2、动画演示

9.3、实现代码
package com.chan.sort;
/**
* 基数排序(升序)
* @author lone_wolf
* @version 1.0
* @date 2021/9/30 22:37
*/
import java.util.Arrays;
public class RadixSort{
public static void main(String[] args){
int[] a = {6, 1, 2, 5, 3, 4};
int[] sort = sort(a);
for (int i : sort) {
System.out.print(" " + i);
}
}
public static int[] sort(int[] sourceArray) {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int maxDigit = getMaxDigit(arr);
return radixSort(arr, maxDigit);
}
/**
* 获取最高位数
*/
private static int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLenght(maxValue);
}
private static int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
protected static int getNumLenght(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
private static int[] radixSort(int[] arr, int maxDigit) {
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
return arr;
}
/**
* 自动扩容,并保存数据
*
* @param arr
* @param value
*/
private static int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}
9.4、总结
平均时间复杂度:O(p(n+b))
算法空间复杂度:O(p(n+b))
算法稳定性:稳定