题目描述
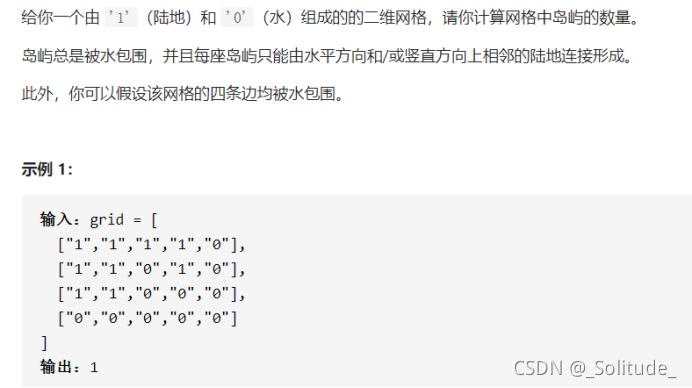
这是一道leetcode上非常经典的题(岛屿数量),解决思路也很多。
DFS解法
DFS解法是用染色的方法,我们遍历每一个节点,每个节点都做这样的事:首先判断岛屿是否被拜访过,没被拜访过则先将岛屿数加一,再利用DFS搜索的方法,将与它连接在一起的每个节点都标记为拜访过,。这样在遍历第一个节点的时候会将与第一个节点相连的节点全都标记为拜访过,之后即使再碰到也会认为属于第一个节点的集群。
//author: Solitude
//date: 2021-07-01
//purpose:solve the island problem by DFS
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
//initialize
int count = 0;
for(int i = 0; i < grid.size(); i++){
for(int j = 0; j < grid[0].size(); j++){
if(grid[i][j] == '1'){
count++;
dfs(grid,i,j);
}
}
}
return count;
}
void dfs(vector<vector<char>>& grid, int i, int j){
cout<<i<<"&"<<j<<endl;
//判断i,j是否为合法值
if(i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] == '0')
return;
grid[i][j] = '0';
dfs(grid,i-1,j);
dfs(grid,i,j+1);
dfs(grid,i+1,j);
dfs(grid,i,j-1);
}
};
BFS解法
BFS解法与DFS解法类似,也是利用染色。只不过把遍历方法换为了BFS
//author: Solitude
//date: 2021-07-01
//purpose:solve the island problem by BFS
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
//initialize
int count = 0;
//
for(int i = 0; i < grid.size(); i++){
for(int j = 0; j < grid[0].size(); j++){
if(grid[i][j] == '1'){
count = count + 1;
bfs(grid,i,j);
}
}
}
return count;
}
void bfs(vector<vector<char>>& grid, int i, int j){
//initialize
grid[i][j] = '0';
queue<vector<int>> q;
q.push({i,j});
vector<int> v;
//bfs
while(!q.empty()){
v = q.front();
q.pop();
if(v[0]-1 >= 0 && grid[v[0]-1][v[1]] == '1')
{
grid[v[0]-1][v[1]] = '0';
q.push({v[0]-1,v[1]});
}
if(v[1]+1 < grid[0].size() && grid[v[0]][v[1]+1] == '1'){
grid[v[0]][v[1]+1] = '0';
q.push({v[0],v[1]+1});
}
if(v[0]+1 < grid.size() && grid[v[0]+1][v[1]] == '1'){
grid[v[0]+1][v[1]] = '0';
q.push({v[0]+1,v[1]});
}
if(v[1]-1 >= 0 && grid[v[0]][v[1]-1] == '1')
{
grid[v[0]][v[1]-1] = '0';
q.push({v[0],v[1]-1});
}
}
}
};
并查集解法
并查集将每个岛屿与周围可以连通的岛屿连接起来。我实现的时候反转了一下思路,利用count记录遍历每个岛屿的,而每次将岛屿与其他的岛屿连接的时候都将count减去1,这样同样能利用count记录最终的岛屿数量。
//author: Solitude
//date: 2021-07-01
//purpose:solve the island problem by union-find sets
class Solution {
public:
vector<int> v;
int count = 0;
int numIslands(vector<vector<char>>& grid) {
int m = grid.size();
int n = grid[0].size();
make(m*n);
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == '1'){
//与上下左右的为1岛屿互联
count++;
if(i-1 >= 0 && grid[i-1][j] == '1')
union_islands(i*n+j,(i-1)*n+j);
if(i+1 < m && grid[i+1][j] == '1')
union_islands(i*n+j,(i+1)*n+j);
if(j-1 >= 0 && grid[i][j-1] == '1')
union_islands(i*n+j,i*n+j-1);
if(j+1 < n && grid[i][j+1] == '1')
union_islands(i*n+j,i*n+j+1);
}
}
}
return count;
}
void make(int n){
//创建并查集
v.resize(n);
for(int i = 0; i < n; i++){
v[i] = i;
}
}
void union_islands(int p, int q){
//合并小岛
int rootp = find_root(p);
int rootq = find_root(q);
if(rootp == rootq)
return;
else{
v[rootq] = rootp;
count--;
}
}
int find_root(int x){
//发现祖先
//root为公共祖先
int root = x;
while(v[root] != root){
root = v[root];
}
//压缩路径
while(v[x] != root){
int temp = v[x];
v[x] = root;
x = temp;
}
return root;
}
};