[数据结构与算法]2021ACM预选赛K题题解

K.涛涛们的烦恼（原2021icpc网络赛第一场K题）

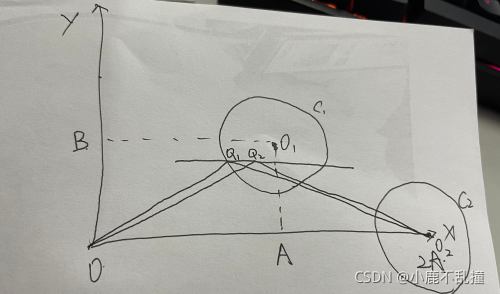
Moon很喜欢吃东西，她在坐标为（A,B)的庄园里堆满了半径为R的零食。每天很多只涛涛都要从原点出发，去Moon的庄园拿零食，并带去坐标为（2A，0）的Moon的城堡。Moon的城堡也是占地为半径为R的圆，涛涛们只需要送到Moon的城堡门口就可以了，涛涛们不知道怎么样走才能最短，你可以帮帮可爱的涛涛们吗？

这是一道数学题，我们可以把它化简为求O到$C_1$内一点加上这一点到$O_2$的最小值减去R。
取任意一条过$C_1$的直线l，先找到当点Q在l上时，OQ+Q$O_2$的最小值，先取l上任意两点$Q_1$，$Q_2$，将O与$Q_1$和$Q_1$与$O_2$和O与$Q_2$和$Q_2$与$O_2$连起来。

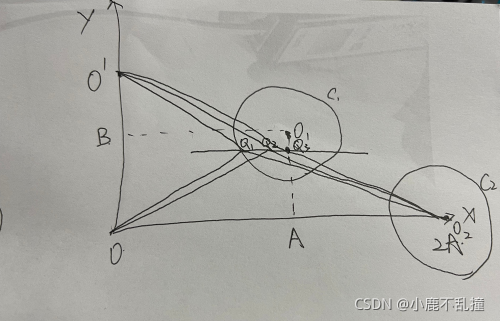
我们可以很明显的想到利用对称性来解决这个问题，做O点关于l的对称点，连起来即为最小距离。

$Q_3$即为所求。易证$Q_3$在O$O_2$的中垂线上。当l在接近x轴的时候显然比远离x的最优，所以显然，$C_1$的最底点即为题目所求。
但是这个只考虑了一种情况，还有一种情况，就是$C_1$与x轴有交点时，直接去$O_2$点显然更近。
其实还有一种$C_1$与$C_2$相交的情况，但是题目的数据规避了这个问题，这种情况可以忽略。
这道题还有一个小小的点，就是因为Moon没有过4级（实际上是涛涛的锅）需要特判一下是第几只涛涛。
下附代码：

```cpp
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
string d[11]={"th","st","nd","rd","th","th","th","th","th","th"};
int main()
{
	int T;
	freopen("2.in","r",stdin);
	freopen("2.out","w",stdout);
	cin>>T;
	for(int t=1;t<=T;t++)
	{
		double a,b,c;
		cin>>a>>b>>c;
		double ans=0;
		if(b<=c)
			ans=2*a-c;
		else
			ans=2*sqrt(a*a+(b-c)*(b-c))-c;
		printf("The shortest path of the %d%s Tekola is %.2f.\n",t,d[t%10].c_str(),ans);
	}
	return 0;
}