[数据结构与算法]二叉树基础（三）树状数组

概念

树状数组（Binary Indexed Tree, Fenwick Tree）是一种用于高效处理对一个存储数字的列表进行更新及求前缀和的数据结构。

$lowbit$运算

$lowbit(x)$是x的二进制表达式中最低位的1所对应的值，比如：

$(6{)}_{10}=(110{)}_2$

若一个数$x$的二进制最低位的1在从右往左数的第$k$位，则

$lowbit(x)=2^{k?1}$

$lowbit()$函数有以下两种常用的实现方式：

int lowbit(int x)
{
    return x&(-x);
}

int lowbit(int x)
{
    return x&(x^(x-1));
}

结构

对于正整数$n$，若其二进制表现形式为

$n=2^{i_1}+2^{i_2}+???+2^{i_m}$ $i_1>i_2>???>i_m$

则可以将$[1,n]$划分为$log$ $n$个区间：

$[1,2^{i_1}],[1+2^{i_1},2^{i_1}+2^{i_2}],???,[1+2^{i_1}+2^{i_2}+???+2^{i_{m?1}},2^{i_1}+2^{i_2}+???+2^{i_m}]$

比如$6=2^2+2^1$

则$6$可以分为$[1,4],[5,6]$两个区间，其区间长度分别为$lowbit(4)=2^2=4,lowbit(6)=2^1=2$

树状数组的结构如下图

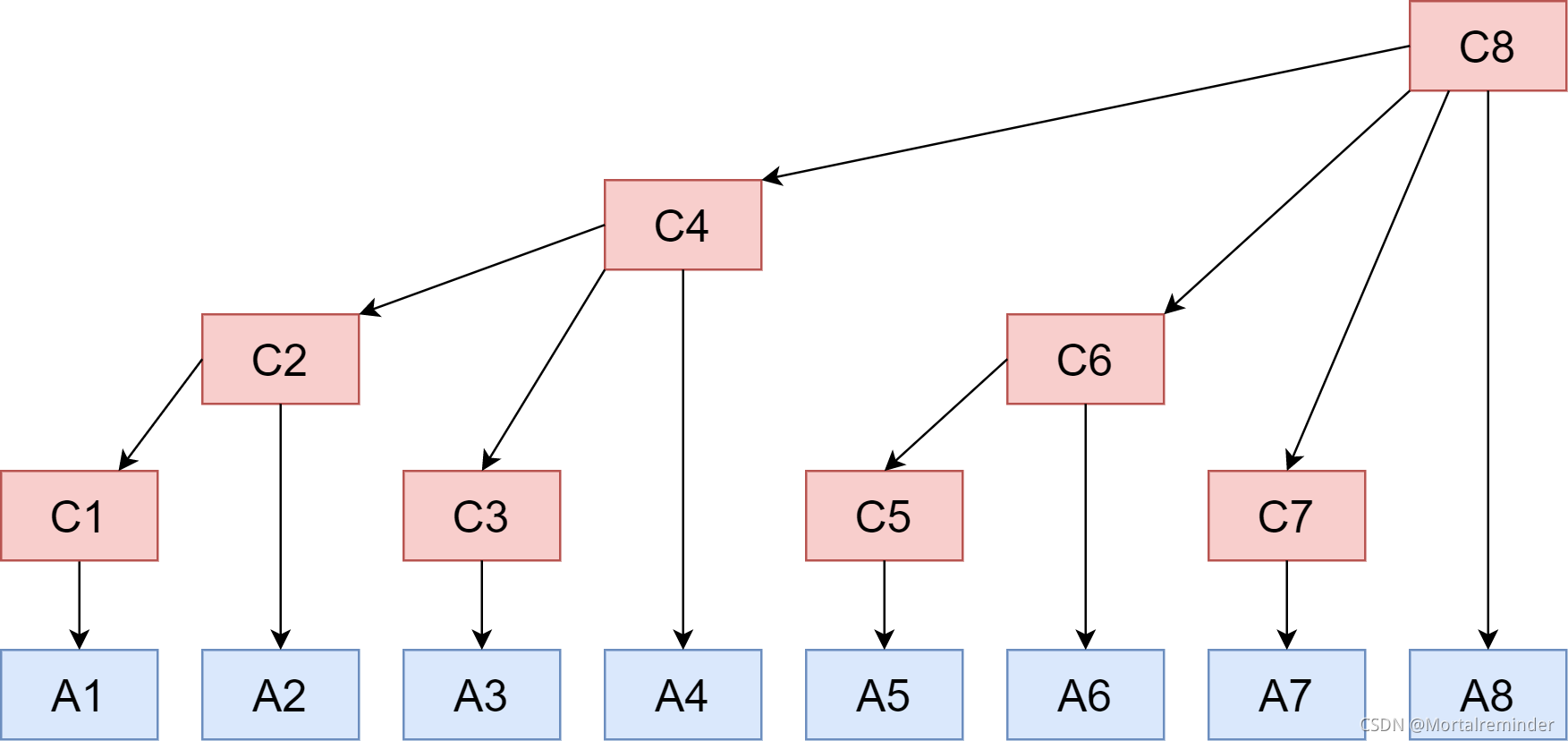
树形数组中存储的为其全部子节点之和，即对于树状数组的节点$t[i]$，有

$t[i]=\sum _{j=i?lowbit(i)+1}^{i}a[j].$

对于位置为$i$的节点，其父节点位置为$i+lowbit(i).$

代码

基本操作

$update()$

在我们使用$update(i,k)$函数时，会从节点$i$开始向上依次更新父节点，比如进行操作，$update(3,2)$时效果如下图：

前面我们已经提到过，父节点的位置为$lowbit(i)$，因此$update()$代码如下

	void update(int i, int k) {
        while (i <= N) { // 从当前结点依次向上更新
            node[i] += k;
            i += lowbit(i);
        }
    }

$sum()$

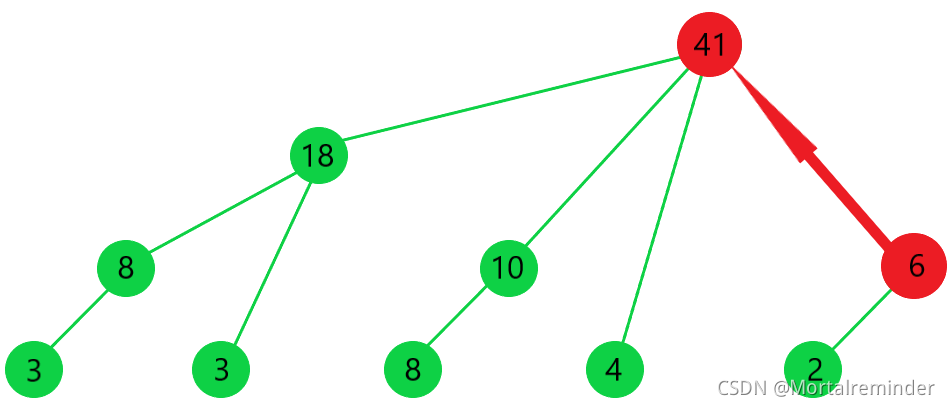
$sum(i)$函数则是从节点$i$不断向下寻找$lowbit(i)$，当我们求$sum(10)$时效果如图

$sum()$函数的代码如下

	int sum(int i) {
        int sum = 0;
        while (i >= 1) { // 依次向下求
            sum += node[i];
            i -= lowbit(i);
        }
        return sum;
    }

若我们想求从$l$到$r$的节点和，只需用$sum(r)$减去$sum(l)$即可

整体代码

class Fenwick {
public:
    int N;
    vector<int> node;

    Fenwick(int n): N(n), node(n+1,0){}

    int lowbit(int i) {
        return i & -i;
    }

    void update(int i, int k) {
        i++;
        while (i <= N) {
            node[i] += k;
            i += lowbit(i);
        }
    }

    int sum(int i) {
        int sum = 0;
        while (i > 0) {
            sum += node[i];
            i -= lowbit(i);
        }
        return sum;
    }

    int sum(int l, int r) {
        return (sum(r)-sum(l));
    }
};