[数据结构与算法]CodeForces_Div2_276_A +鸽巢原理

一.鸽巢原理（抽屉原理）

1.基础点

把ｎ＋１个物体放入n个盒子里，则至少有一个盒子里含有两个或两个以上的物体 。

2.强化点

当n只鸽子飞进m个巢时，必定至少有一个巢中飞进了r只

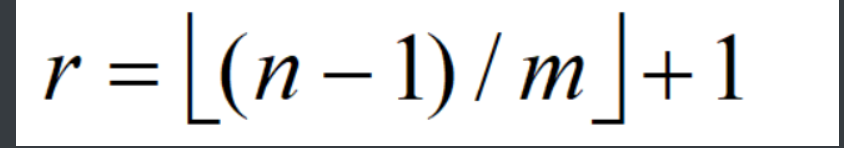
3.运用

只用于证明是否存在的问题

二.Codeforces Round #276 (Div. 2) A.Factory

1.题目的意思是说：第一天有a个材料，每天多生成a%m个材料，当a%m=0时，停止生产计划。

2.暴力可以直接解，比如m是[1,1e5],那么循环1e6就可。

3.找规律，当a%m为前面出现过的余数时，必回陷入循环，则生产不会停止。如果m次内a%m都不为0，则根据鸽巢原理，从m+1次开始，都会出现[1，m]的数，不会出现0，所以循环m次即可。

4.代码（java，c++）

#include<bits/stdc++.h>
using namespace std;

int main(){
    int a,m;
    cin >> a >> m;
    bool stop = false;
    for (int i = 0; i < m; i++){
        int tmp = a % m;
        if (tmp == 0){
            stop = true;
            break;
        }
        a += tmp;
    }
    if (stop)   cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

import java.util.*;
public class D2_276_A{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int a = sc.nextInt();
        int m = sc.nextInt();
        boolean stop = false;
        for (int i = 0; i < m; i++){
            int tmp = a % m;
            if (tmp == 0){
                stop = true;
                break;
            }
            a += a % m;
        }
        if (stop) System.out.println("Yes");
        else System.out.println("No");
        sc.close();
    }
}