题目

给你一个 $\times n$ 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 $k$ 小的元素。
请注意，它是 排序后 的第 $k$ 小元素，而不是第 $k$ 个不同的元素。

示例 1：
输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13
示例 2：
输入：matrix = [[-5]], k = 1
输出：-5
提示：

$n = = m a t r i x . l e n g t h$
$n = = m a t r i x [i] . l e n g t h$
$1 < = n < = 300$
$10^9 <= matrix[i][j] <= 10^9$
题目数据保证 matrix 中的所有行和列都按 非递减顺序 排列
$1 <= k <= n^2$

题解

由题目给出的性质可知，这个矩阵内的元素是从左上到右下递增的（假设矩阵左上角为 matrix[0][0]）。以下图为例：
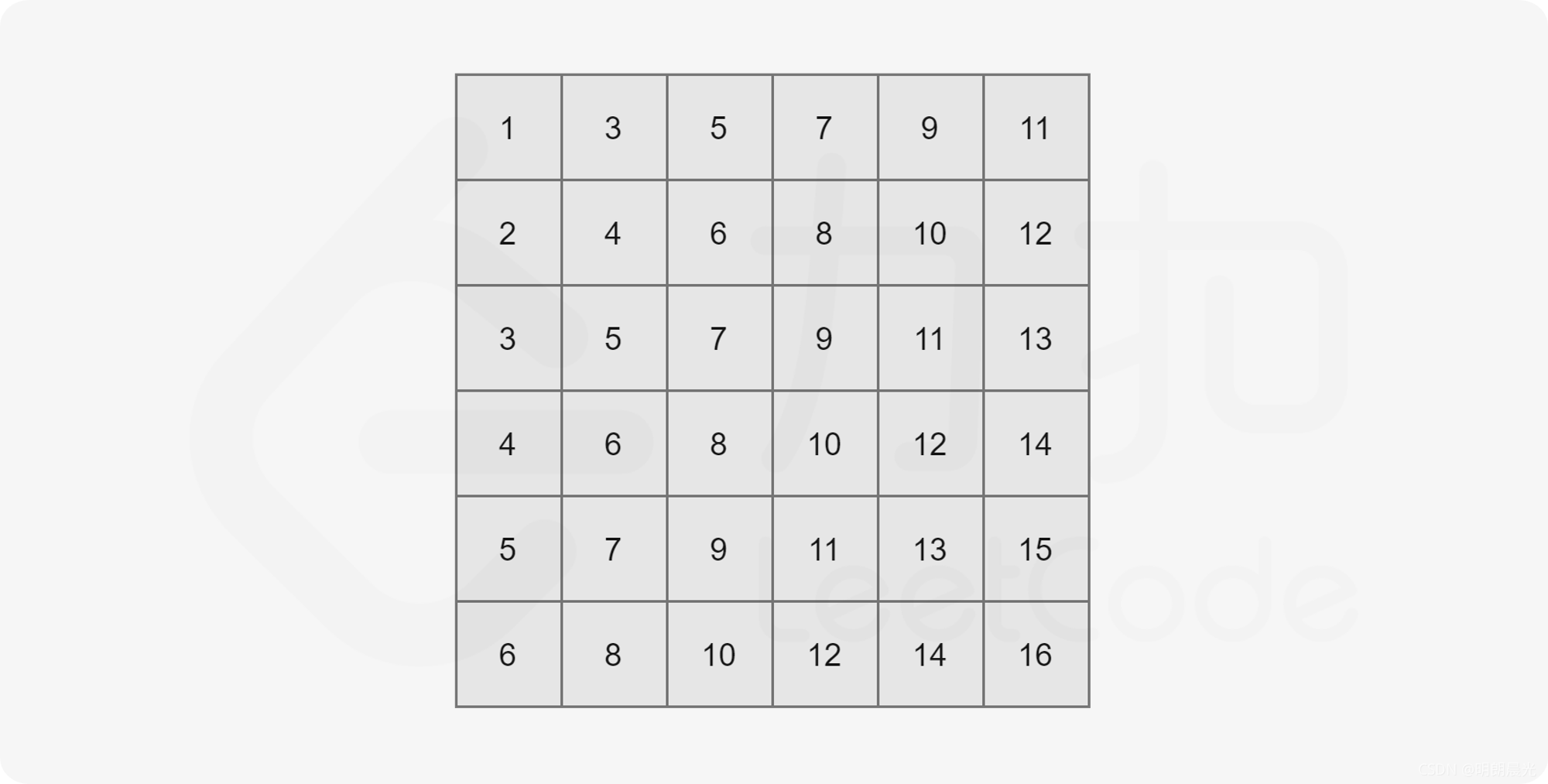
在这里插入图片描述
我们知道整个二维数组中 matrix[0][0]为最小值，matrix[n - 1][n - 1] 为最大值，现在我们将其分别记作 l 和 r。

可以发现一个性质：任取一个数 mid 满足 l ≤ mid ≤ r，那么矩阵中不大于 mid 的数，肯定全部分布在矩阵的左上角。

例如下图，取 mid=8：
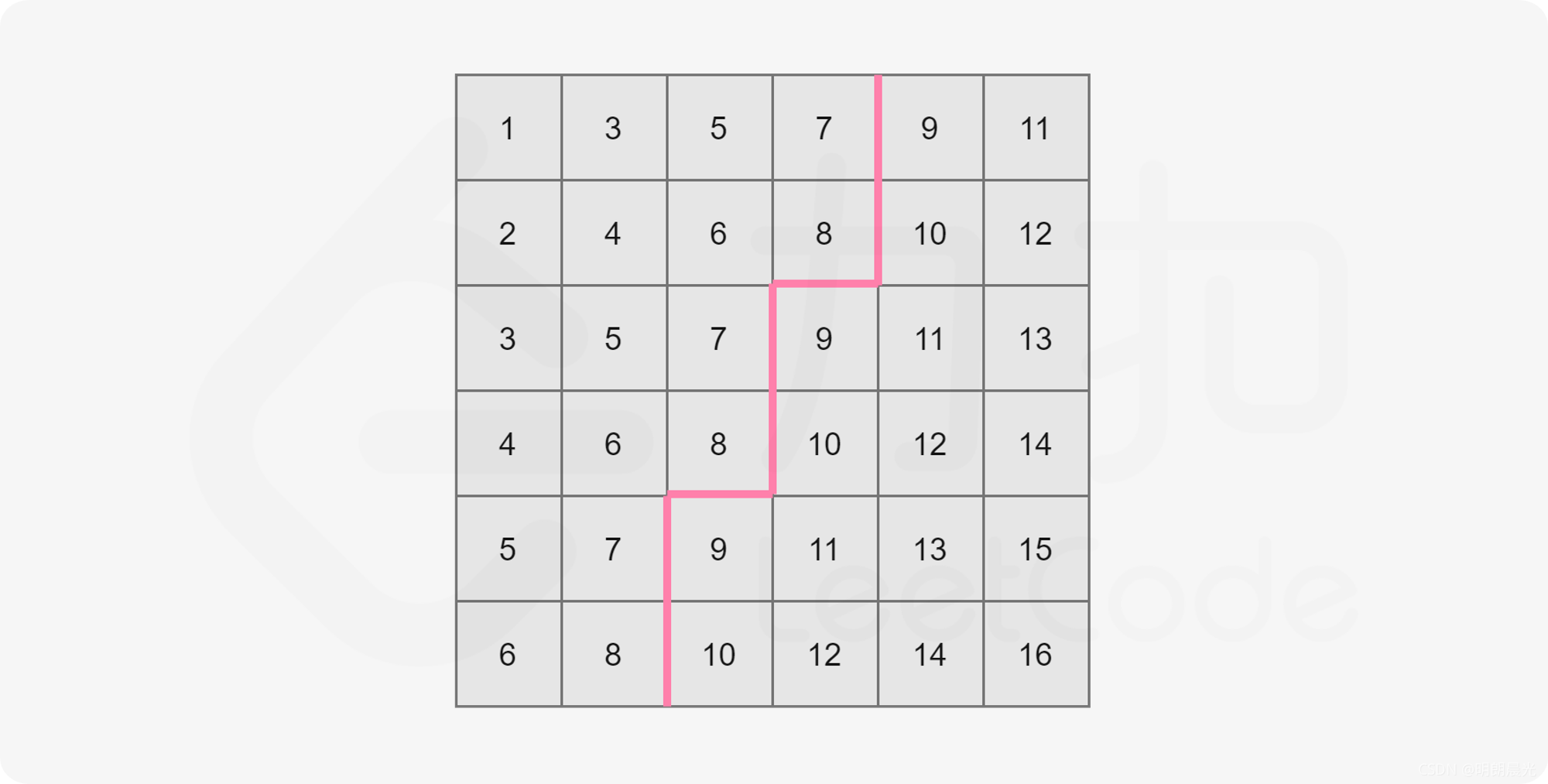
在这里插入图片描述
我们可以看到，矩阵中大于 mid的数就和不大于 mid 的数分别形成了两个板块，沿着一条锯齿线将这个矩形分开。其中左上角板块的大小即为矩阵中不大于 mid 的数的数量。

我们只要沿着这条锯齿线走一遍即可计算出这两个板块的大小，也自然就统计出了这个矩阵中不大于 mid 的数的个数了。

走法演示如下，依然取 mid=8：
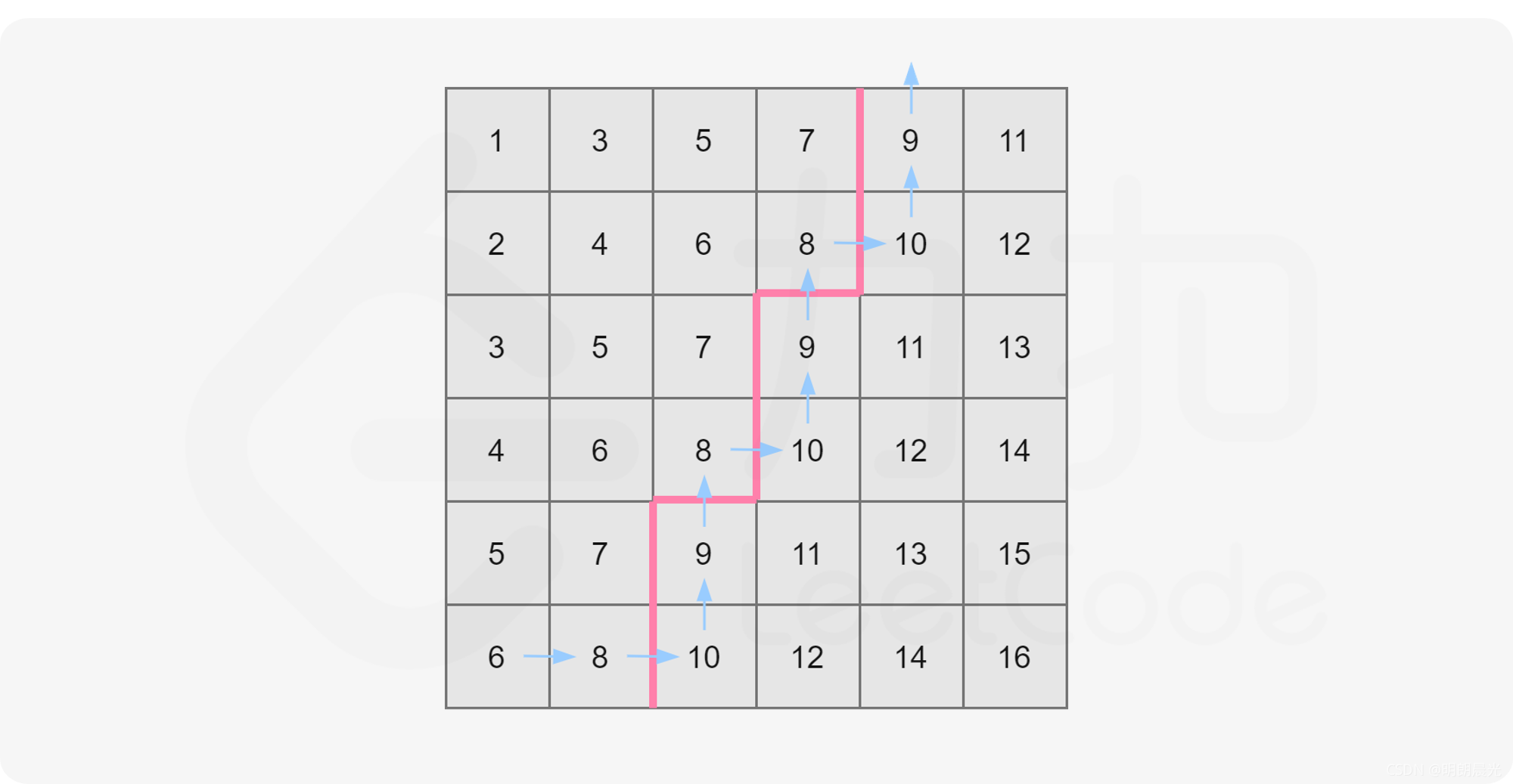
在这里插入图片描述
可以这样描述走法：

初始位置在 matrix[n - 1][0]（即左下角）；
设当前位置为 matrix[i][j]。若 matrix[i][j] ≤ mid，则将当前所在列的不大于 mid 的数的数量（即 i + 1）累加到答案中，并向右移动，否则向上移动；
不断移动直到走出格子为止。

我们发现这样的走法时间复杂度为 $O (n)$ ，即我们可以线性计算对于任意一个 mid，矩阵中有多少数不大于它。这满足了二分查找的性质。

不妨假设答案为 x，那么可以知道 l ≤ x ≤ r，这样就确定了二分查找的上下界。

每次对于「猜测」的答案 mid，计算矩阵中有多少数不大于 mid ：

如果数量不少于 k，那么说明最终答案 x 不大于 mid；
如果数量少于 k，那么说明最终答案 x 大于 mid。

这样我们就可以计算出最终的结果 x 了。

【代码】

class Solution {
public:
    int getCnt(vector<vector<int>>& matrix, int val) { //找到不大于val的数的个数
        int x = matrix.size() - 1, y = 0, cnt = 0;
        while(x >= 0 && y < matrix.size()) {
            if (matrix[x][y] <= val) { //左下角的数
                cnt += x + 1;
                y++;
            } else {
                x--;
            }
        }
        return cnt;
    }

    int kthSmallest(vector<vector<int>>& matrix, int k) {
        int n = matrix.size();
        int left = matrix[0][0], right = matrix[n - 1][n - 1];
        while (left < right) {
            int mid = left + ((right - left) >> 1);
            if (getCnt(matrix, mid) < k) left = mid + 1;
            else right = mid;
        }
        return left;
    }
};