问题再现
假定输入10个整数型数组a[n]中各元素值均在[0,200]区间内,编写一个解法,分别统计落在[0,20),[20,50),[50,80)[80,130),[130,200]各区间内的元素数.
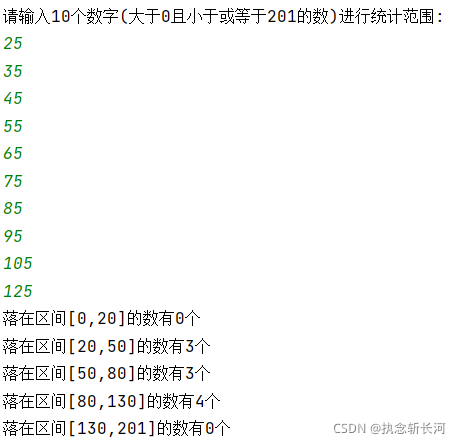
输入输出&代码结果
解法精要
一开始我没在意,觉得这个题目要除以10,结果看完题解才发现,只需要将上限输入倒数组里,用数组与输入样本数据进行比较即可。设置一个存放统计结果的数组int c[5],预先把各元素初始化为0,然后通过一趟扫描,按照数据元素的值,它落在哪个区间,相应统计单元加1,
完整源码
#include<stdio.h>
#define maxSize 10
/*
*a[] 是输入数据数组
* n 是a[]数组的长度
* d[] 是落区域的上限
* c[] 存放的结果数组
* */
void Count(int a[],int n,int d[],int c[]) {
int i,j;
for(i=0;i<5;i++) {
c[i] = 0;
}//初始化结果数组c,赋值为0
for(i=0;i<n;i++) {
for(j=0;j<5;j++) { //查找a[i]的值落在的区间
if(a[i] < d[j])
break;
}
c[j]++; //使统计相应区间的元素加1
}
}
int main() {
int A[maxSize];
printf("请输入10个数字(大于0且小于或等于201的数)进行统计范围:\n");
for(int i= 0;i<maxSize;i++){
scanf("%d",&A[i]);
}
//A[]数据样本
int i,n = maxSize;
int x,y;
int B[5]; //结果数组
int d[5] ={20,50,80,130,201};//用来保存各统计区间的上限
Count(A,n,d,B);
x = 0;
for(i=0;i<5;i++) {
y = d[i];
printf("落在区间[%d,%d]的数有%d个\n",x,y,B[i]);
x = y;
}
return 0;
}
源码跑路
假设输入数据有五个,分别是 25 35 45 55 65,现在主函数调用count参数如下:
- A[]:25 35 45 55 65
- n = 5
- d 20 50 80 130 201
- B 结果数组,不予考虑
count函数首先将c数组进行赋值0,然后进入i和j循环.i<5 j<5
- i=0 25<20不成立 25<50成立所以c[1]+1
- i=1 35<20不成立 35<50成立 所以c[1]+1
- i=2 45<20 不成立 45<50成立 所以c[1]+1
- i=3 55<20 不成立 55<50不成立 55<80成立 c[2]+1
- i=4 65<20 不成立 65<50不成立 ,65<80成立 c[2]+1

好神奇,太神奇了,喜欢这个算法!以后有机会我也用,整除思维太low了。