[数据结构与算法]Java版skiplist跳表详解

skiplist简介

skiplist 是 一个概率型数据结构，查找、删除、插入的时间复杂度都是O(logN)。

skiplist是由多层有序的链表组成的，来加快查找速度。

其中第0层包含了所有元素，然后往上增加了多层的有序链表作为索引来加快查找速度。

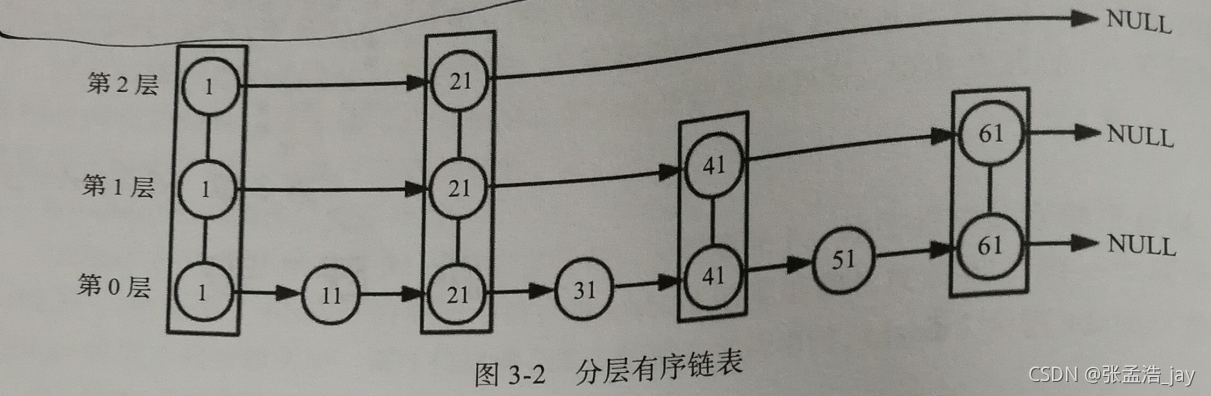
skiplist组成

链表节点Node

public class Node {
        //存储的数据
        private int data = -1;
        /**
         * 表示当前节点位置的下一个节点所有层的数据，从上层切换到下层，就是数组下标-1，
         * forwards[3]表示当前节点在第三层的下一个节点。
         */
        private Node forwards[];
        
        //构造函数，构造一个占据n层的节点
        public Node(int level) {
            forwards = new Node[level];
        }
}

SkipList主要属性

public class SkipList {
    //跳表的允许的最大层数
    private static final int MAX_LEVEL = 16;
    //当前的最大层数
    private int levelCount = 0;
    //跳表的头节点，头节点的层数是最大层
    private Node head = new Node(MAX_LEVEL);
    private Random r = new Random();
}

randomLevel()

skiplist的精髓就在于随机算法，通过随机事件来决定是否为一个节点增加层数，可以灵活的控制索引的数量。如果想要占用少的内存，就可以指定一个小的概率来减少节点的层数。
当然如果节点层数变小，对应的查询效率有可能变慢。

private int randomLevel() {
    int level = 1;
    for (int i = 1; i < MAX_LEVEL; ++i) {
        //如果随机生成的数小于p，就增加层数。
        //如果想要增加目录，就将p赋予一个较大的数。
        if (r.next() < p) {
            level++;
        }
    }
    return level;
}

insert()

public void insert(int value) {
    //获取随机层数
    int level = randomLevel();
    //更新levelCount
    if (level > levelCount) {
        levelCount = level;
    }
    
    Node newNode = new Node(level);
    newNode.data = value;
    Node update[] = new Node[level];
    for (int i = 0; i < level; ++i) {
        update[i] = head;
    }

    Node p = head;
    // 从上层往下层逐层查找，update对应着每层的插入的前一个节点
    for (int i = level - 1; i >= 0; --i) {
        while (p.forwards[i] != null && p.forwards[i].data < value) {
            // 找到前一节点
            p = p.forwards[i];
        }
        //第i层 对应的插入位置 p 
        update[i] = p;

    }
    
    //依次向每层中插入数据
    for (int i = 0; i < level; ++i) {
        newNode.forwards[i] = update[i].forwards[i];
        update[i].forwards[i] = newNode;
    }

}

find()

查找函数，从上层往下层依次查找

public Node find(int value) {
    Node p = head;
    // 从最大层开始查找，找到前一节点，通过--i，移动到下层再开始查找
    for (int i = levelCount - 1; i >= 0; --i) {
        while (p.forwards[i] != null && p.forwards[i].data <= value) {
            // 找到前一节点
            p = p.forwards[i];
        }
    }

    if (p.forwards[0] != null && p.forwards[0].data == value) {
        return p.forwards[0];
    } else {
        return null;
    }
}

delete()

public void delete(int value) {
    Node[] update = new Node[levelCount];
    Node p = head;
    //找到每层的前置节点存储到update中
    for (int i = levelCount - 1; i >= 0; --i) {
        while (p.forwards[i] != null && p.forwards[i].data < value) {
            p = p.forwards[i];
        }
        update[i] = p;
    }
    
    //如果存在对应的元素
    if (p.forwards[0] != null && p.forwards[0].data == value) {
        //为每层更新对应的指针
        for (int i = levelCount - 1; i >= 0; --i) {
            //如果第i层的前置节点的下一个节点是要删除的值，就更新指针
            if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
                update[i].forwards[i] = update[i].forwards[i].forwards[i];
            }
        }
    }
}

总结

通过对应的函数，可以看出，跳表就是一个链表，只不过链表中的节点十分特殊，节点中有一个层数的概念，每一层都对应着有一个指针，指向另一个节点，代表着节点在对应层的下一个节点就是指针代表的节点。

链表查询的缺点就是当查询链表后半部分的数据的时候，需要先遍历前面的节点，这就白白浪费了事件。

跳表的核心思想就是通过随机算法将下层的链表选取部分代表抽取到上层。

这样的话，前半部分的很多元素在高层中会被省略。当查询高层链表的时候，即使是查询后半部分的数据，也可以快速的定位到节点所属的区间。加快了查询效率。